ChatGPT强化学习大杀器——近端策略优化(PPO)
近端策略优化(Proximal Policy Optimization)来自 Proximal Policy Optimization Algorithms(Schulman et. al., 2017)这篇论文,是当前最先进的强化学习 (RL) 算法。这种优雅的算法可以用于各种任务,并且已经在很多项目中得到了应用,最近火爆的ChatGPT就采用了该算法。
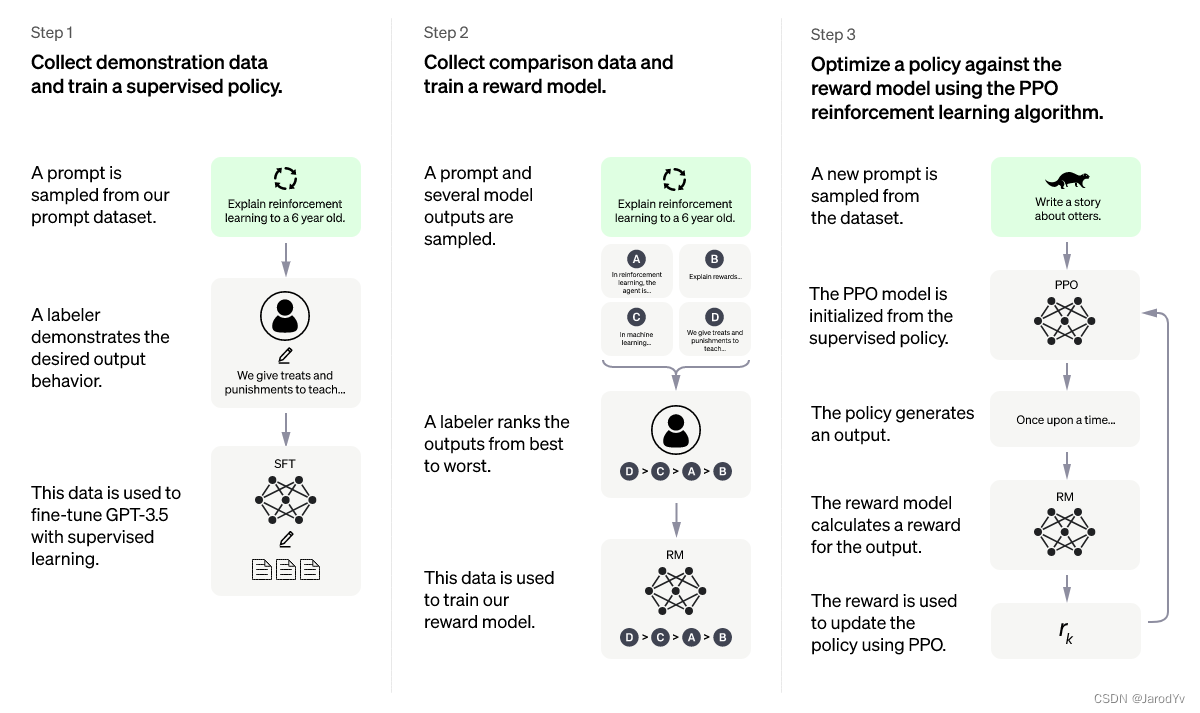
网上讲解ChatGPT算法和训练流程的文章很多,但很少有人深入地将其中关键的近端策略优化算法讲清楚,本文我会重点讲解近端策略优化算法,并用PyTorch从头实现一遍。
文章目录
强化学习
近端策略优化作为一个先进的强化学习算法,我们首先要对强化学习有个了解。关于强化学习,介绍的文章很多,这里我不做过多介绍,但这里我们可以看一下ChatGPT是怎么解释的:

ChatGPT给出的解释比较通俗易懂,更加学术一点的说,强化学习的流程如下:

强化学习框架
上图中,每个时刻环境都会为代理反馈奖励,并监控当前状态。有了这些信息,代理就会在环境中采取行动,然后新的奖励和状态等会反馈给代理,以此形成循环。这个框架非常通用,可以应用于各种领域。
我们的目标是创建一个可以最大化获得奖励的代理。 通常这个最大化奖励是各时间折扣奖励的总和。
G
=
∑
t
=
0
T
γ
t
r
t
G = \sum_{t=0}^T\gamma^tr_t
G=t=0∑Tγtrt
这里
γ
\gamma
γ是折扣因子,通常在 [0.95, 0.99] 范围内,
r
t
r_t
rt 是时间 t 的奖励。
算法
那么我们如何解决强化学习问题呢? 有多种算法,可以(对于马尔可夫决策过程或 MDP)分为两类:基于模型(创建环境模型)和无模型(仅给定状态学习)。
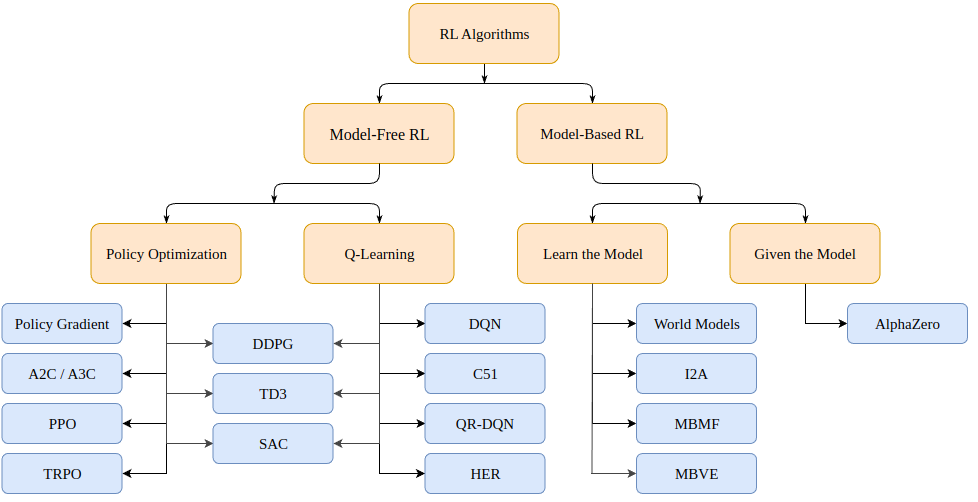
强化学习算法分类
基于模型的算法创建环境模型并使用该模型来预测未来状态和奖励。 该模型要么是给定的(例如棋盘),要么是学习的。
无模型算法直接学习如何针对训练期间遇到的状态(策略优化或 PO)采取行动,哪些状态-行动会产生良好的回报(Q-Learning)。
我们今天讨论的近端策略优化算法属于 PO 算法家族。 因此,我们不需要环境模型来驱动学习。PO 和 Q-Learning 算法之间的主要区别在于 PO 算法可以用于具有连续动作空间的环境(即我们的动作具有真实值)并且即使该策略是随机策略(即按概率行事)也可以找到最优策略;而 Q-Learning 算法不能做这两件事。 这是PO 算法更受欢迎的另一个原因。 另一方面,Q-Learning 算法往往更简单、更直观且更易于训练。
策略优化(基于梯度)
策略优化算法可以直接学习策略。 为此,策略优化可以使用无梯度算法(例如遗传算法),也可以使用更常见的基于梯度的算法。
通过基于梯度的方法,我们指的是所有尝试估计学习策略相对于累积奖励的梯度的方法。 如果我们知道这个梯度(或它的近似值),我们可以简单地将策略的参数移向梯度的方向以最大化奖励。
策略梯度方法通过重复估计梯度
g
:
=
∇
θ
E
[
∑
t
=
0
∞
r
t
]
g:=\nabla_\theta\mathbb{E}[\sum_{t=0}^{\infin}r_t]
g:=∇θE[∑t=0∞rt]来最大化预期总奖励。策略梯度有几种不同的相关表达式,其形式为:
g
=
E
[
∑
t
=
0
∞
Ψ
t
∇
θ
l
o
g
π
θ
(
a
t
∣
s
t
)
]
(1)
g=\mathbb{E}\Bigg\lbrack \sum_{t=0}^{\infin} \Psi_t \nabla_\theta log\pi_\theta(a_t \mid s_t) \Bigg\rbrack \tag{1}
g=E[t=0∑∞Ψt∇θlogπθ(at∣st)](1)
其中
Ψ
t
\Psi_t
Ψt 可以是如下几个:
∑ t = 0 ∞ r t \sum_{t=0}^\infin r_t ∑t=0∞rt: 轨迹的总奖励∑ t ′ = t ∞ r t ′ \sum_{t'=t}^\infin r_{t'} ∑t′=t∞rt′: 下一个动作 a t a_t at 的奖励∑ t = 0 ∞ r t − b ( s t ) \sum_{t=0}^\infin r_t - b(s_t) ∑t=0∞rt−b(st): 上面公式的基线版本Q π ( s t , a t ) Q^\pi(s_t, a_t) Qπ(st,at): 状态-动作价值函数A π ( s t , a t ) A^\pi(s_t, a_t) Aπ(st,at): 优势函数r t + V π ( s t + 1 ) + V π ( s t ) r_t+V^\pi(s_{t+1})+V^\pi(s_{t}) rt+Vπ(st+1)+Vπ(st): TD残差
后面3个公式的具体定义如下:
V
π
(
s
t
)
:
=
E
s
t
+
1
:
∞
,
a
t
:
∞
[
∑
l
=
0
∞
r
t
+
l
]
Q
π
(
s
t
,
a
t
)
:
=
E
s
t
+
1
:
∞
,
a
t
+
1
:
∞
[
∑
l
=
0
∞
r
t
+
l
]
(2)
V^\pi(s_t) := \mathbb{E}_{s_{t+1:\infin}, a_{t:\infin}}\Bigg\lbrack\sum_{l=0}^\infin r_{t+l} \Bigg\rbrack \\ Q^\pi(s_t, a_t) := \mathbb{E}_{s_{t+1:\infin}, a_{t+1:\infin}}\Bigg\lbrack\sum_{l=0}^\infin r_{t+l} \Bigg\rbrack \tag{2}
Vπ(st):=Est+1:∞,at:∞[l=0∑∞rt+l]Qπ(st,at):=Est+1:∞,at+1:∞[l=0∑∞rt+l](2)
A
π
(
s
t
,
a
t
)
:
=
Q
π
(
s
t
,
a
t
)
−
V
π
(
s
t
)
(3)
A^\pi(s_t, a_t) := Q^\pi(s_t, a_t) - V^\pi(s_t) \tag{3}
Aπ(st,at):=Qπ(st,at)−Vπ(st)(3)
请注意,有多种方法可以估计梯度。 在这里,我们列出了 6 个不同的值:总奖励、后继动作的奖励、减去基线版本的奖励、状态-动作价值函数、优势函数(在原始 PPO 论文中使用)和时间差 (TD) 残差。我们可以选择这些值作为我们的最大化目标。 原则上,它们都提供了我们所关注的真实梯度的估计。
近端策略优化
近端策略优化简称PPO,是一种(无模型)基于策略优化梯度的算法。 该算法旨在学习一种策略,可以根据训练期间的经验最大化获得的累积奖励。
它由一个参与者(actor)
π
θ
(
.
∣
s
t
)
\pi\theta(. \mid st)
πθ(.∣st) 和一个**评估者(critic)**
V
(
s
t
)
V(st)
V(st)组成。前者在时间
t
t
t 处输出下一个动作的概率分布,后者估计该状态的预期累积奖励(标量)。 由于 actor 和 critic 都将状态作为输入,因此可以在提取高级特征的两个网络之间共享骨干架构。
PPO 旨在使策略选择具有更高“优势”的行动,即具有比评估者预测的高得多的累积奖励。 同时,我们也不希望一次更新策略太多,这样很可能会出现优化问题。 最后,如果策略具有高熵,我们会倾向于给与额外奖励,以激励更多探索。
总损失函数由三项组成:CLIP项、价值函数 (VF) 项和熵奖励项。最终目标如下:
L
t
C
L
I
P
+
V
F
+
S
(
θ
)
=
E
^
t
[
L
t
C
L
I
P
(
θ
)
−
c
1
L
t
V
F
(
θ
)
+
c
2
S
[
π
θ
]
(
s
t
)
]
L_t^{CLIP+VF+S}(\theta) = \hat{\mathbb{E}}_t \Big\lbrack L_t^{CLIP}(\theta) - c_1L_t^{VF}(\theta)+c_2S[\pi_\theta](s_t)\Big\rbrack
LtCLIP+VF+S(θ)=E^t[LtCLIP(θ)−c1LtVF(θ)+c2S[πθ](st)]
其中
c
1
c_1
c1 和
c
2
c_2
c2 是超参,分别衡量策略评估(critic)和探索(exploration)准确性的重要性。
CLIP项
正如我们所说,损失函数激发行为概率最大化(或最小化),从而导致行为正面优势(或负面优势)
L
C
L
I
P
(
θ
)
=
E
^
t
[
m
i
n
(
r
t
(
θ
)
A
t
^
,
c
l
i
p
(
r
t
(
θ
)
,
1
−
ϵ
,
1
+
ϵ
)
A
^
t
)
]
L^{CLIP}(\theta) = \hat{\mathbb{E}}_t\Big\lbrack min \Big\lparen r_t(\theta)\hat{A_t},clip \big\lparen r_t(\theta),1-\epsilon, 1+\epsilon\big\rparen \hat{A}_t \Big\rparen \Big\rbrack
LCLIP(θ)=E^t[min(rt(θ)At^,clip(rt(θ),1−ϵ,1+ϵ)A^t)]
其中:
r
t
(
θ
)
=
π
θ
(
a
t
∣
s
t
)
π
θ
o
l
d
(
a
t
∣
s
t
)
r_t(\theta) = \frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{old}}(a_t \mid s_t)}
rt(θ)=πθold(at∣st)πθ(at∣st)
是衡量我们现在(更新后的策略)相对于之前执行该先前操作的可能性的比率。 原则上,我们不希望这个系数太大,因为太大意味着策略突然改变。这就是为什么我们采用其最小值和
[
1
−
ϵ
,
1
+
ϵ
]
[1-\epsilon, 1+\epsilon]
[1−ϵ,1+ϵ] 之间的裁剪版本,其中
ϵ
\epsilon
ϵ 是个超参。
优势(advantage)的计算公式如下:
A
^
t
=
−
V
(
s
t
)
+
r
t
+
γ
r
t
+
1
+
γ
2
r
t
+
2
+
⋯
+
γ
(
T
−
t
+
1
)
r
T
−
1
+
γ
T
−
t
V
(
s
T
)
\hat{A}_t = -V(s_t)+r_t+\gamma r_{t+1}+\gamma^2 r_{t+2}+\dots+\gamma^{(T-t+1)} r_{T-1} + \gamma^{T-t}V(s_T)
A^t=−V(st)+rt+γrt+1+γ2rt+2+⋯+γ(T−t+1)rT−1+γT−tV(sT)
其中:
A
t
^
\hat{A_t}
At^ 是估计的优势,
−
V
(
s
t
)
-V(s_t)
−V(st) 是估计的初始状态值,
γ
T
−
t
V
(
s
T
)
\gamma^{T-t}V(s_T)
γT−tV(sT) 是估计的终末状态值,中间部分是过程中观测到的累计奖励。
我们看到它只是衡量评估者对给定状态
s
t
s_t
st 的错误程度。 如果我们获得更高的累积奖励,则优势估计将为正,我们将更有可能在这种状态下采取行动。 反之亦然,如果我们期望更高的奖励但我们得到的奖励更小,则优势估计将为负,我们将降低在此步骤中采取行动的可能性。
请注意,如果我们一直走到终末状态
s
T
s_T
sT,我们就不再需要依赖评估者了,我们可以简单地将评估者与实际累积奖励进行比较。 在这种情况下,优势的估计就是真正的优势。
价值函数项
为了对优势有一个良好的估计,我们需要一个可以预测给定状态值的评估者。 该模型为具有简单 MSE 损失的监督学习:
L
t
V
F
=
M
S
E
(
r
t
+
γ
r
t
+
1
+
⋯
+
γ
(
T
−
t
+
1
)
r
T
−
1
+
V
(
s
T
)
,
V
(
s
t
)
)
=
∣
∣
A
^
t
∣
∣
2
L_t^{VF} = MSE(r_t+\gamma r_{t+1}+\dots+\gamma^{(T-t+1)} r_{T-1}+V(s_T),V(s_t)) = ||\hat{A}_t||_2
LtVF=MSE(rt+γrt+1+⋯+γ(T−t+1)rT−1+V(sT),V(st))=∣∣A^t∣∣2
每次迭代中,我们也会更新评估者,以便随着训练的进行,它会为我们提供越来越准确的状态值。
熵奖励项
最后,我们鼓励对策略输出分布的熵进行少量奖励的探索。 标准熵为:
S
[
π
θ
]
(
s
t
)
=
−
∫
π
θ
(
a
t
∣
s
t
)
l
o
g
(
π
θ
(
a
t
∣
s
t
)
)
d
a
t
S[\pi_\theta](s_t) = -\int \pi_\theta(a_t \mid s_t) log(\pi_\theta(a_t \mid s_t))da_t
S[πθ](st)=−∫πθ(at∣st)log(πθ(at∣st))dat
算法实现
如果上面的讲解不够清晰,不用担心,下面将带大家从零开始一步一步实现近端策略优化算法。
工具代码
首先先导入所需的库
from argparse import ArgumentParser
import gym
import numpy as np
import wandb
import torch
import torch.nn as nn
from torch.optim import Adam
from torch.optim.lr_scheduler import LinearLR
from torch.distributions.categorical import Categorical
import pytorch_lightning as pl
PPO 的重要超参有 actor 数量、horizon、epsilon、每个优化阶段的 epoch 数量、学习率、折扣因子gamma以及权衡不同损失项的常数 c1 和 c2。 这些超参我们通过参数传入进来。
defparse_args():"""解析参数"""
parser = ArgumentParser()
parser.add_argument("--max_iterations",type=int,help="训练迭代次数", default=100)
parser.add_argument("--n_actors",type=int,help="actor数量", default=8)
parser.add_argument("--horizon",type=int,help="每个actor的时间戳数量", default=128)
parser.add_argument("--epsilon",type=float,help="Epsilon", default=0.1)
parser.add_argument("--n_epochs",type=int,help="每次迭代的训练轮数", default=3)
parser.add_argument("--batch_size",type=int,help="Batch size", default=32*8)
parser.add_argument("--lr",type=float,help="学习率", default=2.5*1e-4)
parser.add_argument("--gamma",type=float,help="折扣因子gamma", default=0.99)
parser.add_argument("--c1",type=float,help="损失函数价值函数的权重", default=1)
parser.add_argument("--c2",type=float,help="损失函数熵奖励的权重", default=0.01)
parser.add_argument("--n_test_episodes",type=int,help="Number of episodes to render", default=5)
parser.add_argument("--seed",type=int,help="随机种子", default=0)returnvars(parser.parse_args())
请注意,默认情况下,参数是按照论文中的描述设置的。 理想情况下,我们的代码应该尽可能在 GPU 上运行,因此我们需要设置一下torch的设备。
defget_device():if torch.cuda.is_available():
device = torch.device("cuda")print(f"Found GPU device: {torch.cuda.get_device_name(device)}")else:
device = torch.device("cpu")print("No GPU found: Running on CPU")return device
当我们执行强化学习时,通常会设一个缓冲区来存储当前模型遇到的状态、动作和奖励,用于更新我们的模型。 我们创建一个函数
run_timestamps
,它将在给定的环境中运行给定的模型并获得固定数量的时间戳(如果episode 结束则重新设置环境)。 我们还使用选项
render=False
以便我们只想查看训练模型的表现。
@torch.no_grad()defrun_timestamps(env, model, timestamps=128, render=False, device="cpu"):"""针对给定数量的时间戳在给定环境中运行给定策略。
返回具有状态、动作和奖励的缓冲区。"""buffer=[]
state = env.reset()[0]# 运行时间戳并收集状态、动作、奖励和终止for ts inrange(timestamps):
model_input = torch.from_numpy(state).unsqueeze(0).to(device).float()
action, action_logits, value = model(model_input)
new_state, reward, terminated, truncated, info = env.step(action.item())# (s, a, r, t)渲染到环境或存储到bufferif render:
env.render()else:buffer.append([model_input, action, action_logits, value, reward, terminated or truncated])# 更新当前状态
state = new_state
# 如果episode终止或被截断,则重置环境if terminated or truncated:
state = env.reset()[0]returnbuffer
该函数的返回值(未渲染时)是一个缓冲区,其中包含状态、采取的行动、行动概率(logits)、评估者价值、奖励以及每个时间戳所提供策略的终止状态。 请注意,该函数使用装饰器
@torch.no_grad()
,因此我们不需要为与环境交互期间采取的操作存储梯度。
核心代码
有了上面的工具函数,我们就可以开发近端策略优化的核心代码了。首先新搭建main函数流程:
defmain():# 解析参数
args = parse_args()print(args)# 设置种子
pl.seed_everything(args["seed"])# 获取设备
device = get_device()# 创建环境
env_name ="CartPole-v1"
env = gym.make(env_name)# TODO 创建模型,训练模型,输出结果
model = MyPPO(env.observation_space.shape, env.action_space.n).to(device)
training_loop(env, model, args)
model = load_best_model()
testing_loop(env, model)
上面就是整体程序的流程框架。接下来,我们只需要定义 PPO 模型、训练和测试函数。
PPO 模型的架构这里不过多阐述,我们只需要两个在环境中起作用的模型(actor和critic)。 当然,模型架构在更复杂的任务中作用至关重要,但有我们这个简单任务中,MLP 就可以完成这项工作。
因此,我们可以创建一个包含actor和critic模型的
MyPPO
类。当对某些状态运行前向方法时,我们返回actor的采样动作、每个可能动作的相对概率 (logits) 以及critic对每个状态的估计值。
classMyPPO(nn.Module):"""
PPO模型的实现。
相同的代码结构即可用于actor,也可用于critic。
"""def__init__(self, in_shape, n_actions, hidden_d=100, share_backbone=False):# 父类构造函数super(MyPPO, self).__init__()# 属性
self.in_shape = in_shape
self.n_actions = n_actions
self.hidden_d = hidden_d
self.share_backbone = share_backbone
# 共享策略主干和价值函数
in_dim = np.prod(in_shape)defto_features():return nn.Sequential(
nn.Flatten(),
nn.Linear(in_dim, hidden_d),
nn.ReLU(),
nn.Linear(hidden_d, hidden_d),
nn.ReLU())
self.backbone = to_features()if self.share_backbone else nn.Identity()# State action function
self.actor = nn.Sequential(
nn.Identity()if self.share_backbone else to_features(),
nn.Linear(hidden_d, hidden_d),
nn.ReLU(),
nn.Linear(hidden_d, n_actions),
nn.Softmax(dim=-1))# Value function
self.critic = nn.Sequential(
nn.Identity()if self.share_backbone else to_features(),
nn.Linear(hidden_d, hidden_d),
nn.ReLU(),
nn.Linear(hidden_d,1))defforward(self, x):
features = self.backbone(x)
action = self.actor(features)
value = self.critic(features)return Categorical(action).sample(), action, value
请注意,
Categorical(action).sample()
创建了一个分类分布,其中包含一个动作(针对每个状态)的动作 logits 和样本。
最后,我们可以处理
training_loop
函数中的实际算法。 正如我们从论文中了解到的,该函数的实际签名应如下所示:
deftraining_loop(env, model, max_iterations, n_actors, horizon, gamma,
epsilon, n_epochs, batch_size, lr, c1, c2, device, env_name=""):# TODO...
以下是论文中为 PPO 训练程序的伪代码:

PPO 的伪代码相对简单:我们只需通过策略模型(称为actor)的多个副本收集与环境的交互,并使用先前定义的目标来优化actor和critic网络。
由于我们需要衡量我们真正获得的累积奖励,因此需要创建一个函数,给定一个缓冲区,用累积奖励替换每个时间的奖励:
defcompute_cumulative_rewards(buffer, gamma):"""
给定一个包含状态、策略操作逻辑、奖励和终止的缓冲区,计算每个时间的累积奖励并将它们代入缓冲区。
"""
curr_rew =0.# 反向遍历缓冲区for i inrange(len(buffer)-1,-1,-1):
r, t =buffer[i][-2],buffer[i][-1]if t:
curr_rew =0else:
curr_rew = r + gamma * curr_rew
buffer[i][-2]= curr_rew
# 在规范化之前获得平均奖励(用于日志记录和检查点)
avg_rew = np.mean([buffer[i][-2]for i inrange(len(buffer))])# 规范化累积奖励
mean = np.mean([buffer[i][-2]for i inrange(len(buffer))])
std = np.std([buffer[i][-2]for i inrange(len(buffer))])+1e-6for i inrange(len(buffer)):buffer[i][-2]=(buffer[i][-2]- mean)/ std
return avg_rew
请注意,最后我们将累积奖励归一化处理。 这是使优化问题更容易和训练更顺利的标准技巧。
现在我们可以获得包含状态、采取的动作、动作概率和累积奖励的缓冲区,可以编写一个函数,在给定缓冲区的情况下,为我们的最终目标计算三个损失项:
defget_losses(model, batch, epsilon, annealing, device="cpu"):"""给定模型、给定批次和附加参数返回三个损失项"""# 获取旧数据
n =len(batch)
states = torch.cat([batch[i][0]for i inrange(n)])
actions = torch.cat([batch[i][1]for i inrange(n)]).view(n,1)
logits = torch.cat([batch[i][2]for i inrange(n)])
values = torch.cat([batch[i][3]for i inrange(n)])
cumulative_rewards = torch.tensor([batch[i][-2]for i inrange(n)]).view(-1,1).float().to(device)# 使用新模型计算预测
_, new_logits, new_values = model(states)# 状态动作函数损失(L_CLIP)
advantages = cumulative_rewards - values
margin = epsilon * annealing
ratios = new_logits.gather(1, actions)/ logits.gather(1, actions)
l_clip = torch.mean(
torch.min(
torch.cat((ratios * advantages,
torch.clip(ratios,1- margin,1+ margin)* advantages),
dim=1),
dim=1).values
)# 价值函数损失(L_VF)
l_vf = torch.mean((cumulative_rewards - new_values)**2)# 熵奖励
entropy_bonus = torch.mean(torch.sum(-new_logits *(torch.log(new_logits +1e-5)), dim=1))return l_clip, l_vf, entropy_bonus
请注意,在实践中,我们使用初值为 1 并在整个训练过程中线性衰减至 0 的退火参数。 因为随着训练的进行,我们希望我们的策略变化越来越少。 另外,与
new_logits
和
new_values
不同,我们不不跟踪
advantages
变量的梯度,只是张量之差。
现在我们有了环境交互和存储缓冲区、计算(真实)累积奖励并获得损失项的方法,可以着手编写最终训练代码了:
deftraining_loop(env, model, max_iterations, n_actors, horizon, gamma, epsilon, n_epochs, batch_size, lr,
c1, c2, device, env_name=""):"""使用最多n个时间戳的多个actor在给定环境中训练模型。"""# 开始运行新的权重和偏差
wandb.init(project="Papers Re-implementations",
entity="peutlefaire",
name=f"PPO - {env_name}",
config={"env":str(env),"number of actors": n_actors,"horizon": horizon,"gamma": gamma,"epsilon": epsilon,"epochs": n_epochs,"batch size": batch_size,"learning rate": lr,"c1": c1,"c2": c2
})# 训练变量
max_reward =float("-inf")
optimizer = Adam(model.parameters(), lr=lr, maximize=True)
scheduler = LinearLR(optimizer,1,0, max_iterations * n_epochs)
anneals = np.linspace(1,0, max_iterations)# 训练循环for iteration inrange(max_iterations):buffer=[]
annealing = anneals[iteration]# 使用当前策略收集所有actor的时间戳for actor inrange(1, n_actors +1):buffer.extend(run_timestamps(env, model, horizon,False, device))# 计算累积奖励并刷新缓冲区
avg_rew = compute_cumulative_rewards(buffer, gamma)
np.random.shuffle(buffer)# 运行几轮优化for epoch inrange(n_epochs):for batch_idx inrange(len(buffer)// batch_size):
start = batch_size * batch_idx
end = start + batch_size if start + batch_size <len(buffer)else-1
batch =buffer[start:end]# 归零优化器梯度
optimizer.zero_grad()# 获取损失
l_clip, l_vf, entropy_bonus = get_losses(model, batch, epsilon, annealing, device)# 计算总损失并反向传播
loss = l_clip - c1 * l_vf + c2 * entropy_bonus
loss.backward()# 优化
optimizer.step()
scheduler.step()# 记录输出
curr_loss = loss.item()
log =f"Iteration {iteration +1} / {max_iterations}: " \
f"Average Reward: {avg_rew:.2f}\t" \
f"Loss: {curr_loss:.3f} " \
f"(L_CLIP: {l_clip.item():.1f} | L_VF: {l_vf.item():.1f} | L_bonus: {entropy_bonus.item():.1f})"if avg_rew > max_reward:
torch.save(model.state_dict(), MODEL_PATH)
max_reward = avg_rew
log +=" --> Stored model with highest average reward"print(log)# 将信息记录到 W&B
wandb.log({"loss (total)": curr_loss,"loss (clip)": l_clip.item(),"loss (vf)": l_vf.item(),"loss (entropy bonus)": entropy_bonus.item(),"average reward": avg_rew
})# 完成 W&B 会话
wandb.finish()
最后,为了查看模型的最终效果,我们使用以下
testing_loop
函数:
deftesting_loop(env, model, n_episodes, device):for _ inrange(n_episodes):
run_timestamps(env, model, timestamps=128, render=True, device=device)
这样,我们的主程序就会变得很简单:
defmain():# 解析参数
args = parse_args()print(args)# 设置种子
pl.seed_everything(args["seed"])# 获取设备
device = get_device()# 创建环境
env_name ="CartPole-v1"
env = gym.make(env_name)# 创建模型(actor和critic)
model = MyPPO(env.observation_space.shape, env.action_space.n).to(device)# 训练
training_loop(env, model, args["max_iterations"], args["n_actors"], args["horizon"], args["gamma"], args["epsilon"],
args["n_epochs"], args["batch_size"], args["lr"], args["c1"], args["c2"], device, env_name)# 加载最佳模型
model = MyPPO(env.observation_space.shape, env.action_space.n).to(device)
model.load_state_dict(torch.load(MODEL_PATH, map_location=device))# 测试
env = gym.make(env_name, render_mode="human")
testing_loop(env, model, args["n_test_episodes"], device)
env.close()
以上这就是全部的实现! 如果你理解上面的代码,恭喜你,你已经理解PPO算法了。
结论
近端策略优化是最先进的策略强化学习优化算法,它几乎可以在任何环境中使用。 此外,近端策略优化具有相对简单的目标函数和相对较少的需要调整的超参。
ChatGPT依赖PPO在第三步获得了超出预期的效果,大家可以在自己的强化学习任务中予以采用,可能会获得意想不到的效果。
版权归原作者 JarodYv 所有, 如有侵权,请联系我们删除。