在本文中,我们将在PyTorch中为Chain Reaction[2]游戏从头开始实现DeepMind的AlphaZero[1]。为了使AlphaZero的学习过程更有效,我们还将使用一个相对较新的改进,称为“Playout Cap Randomization”[3],以及来自[4]的一些其他技术。在训练过程中,将使用并行处理来并行模拟多个游戏,还将通过一些相关的研究论文讨论AlphaZero的未来发展方向。
本文目的不是用AlphaZero构建最好的游戏机器人机器人(因为这需要大量的计算资源),而是构建一个像样的机器人,至少可以击败随机的Agent,以Chain Reaction游戏为例了解AlphaZero是如何工作的。
本节首先解释Chain Reaction游戏是如何工作的。如果你只是想了解AlphaZero的工作原理,请跳过下一节直接转到AlphaZero部分。
Chain Reaction
首先我们从理解Chain Reaction游戏开始,这是一个完美的信息游戏,经过几步之后的游戏对我们来说看起来非常混乱和不可预测。所以我很好奇AlphaZero在这游戏中训练后会有多强大。Chain Reaction可以在许多玩家中进行,但在本文中将局限于两个玩家。
游戏规则
让我们从这个游戏的规则开始。有一个M行N列的棋盘,两名玩家。每个玩家都有一种指定的颜色。出于本文的目的,假设我们有一个红色玩家和一个绿色玩家,红色玩家先走。下图显示了游戏中的一些中间状态。
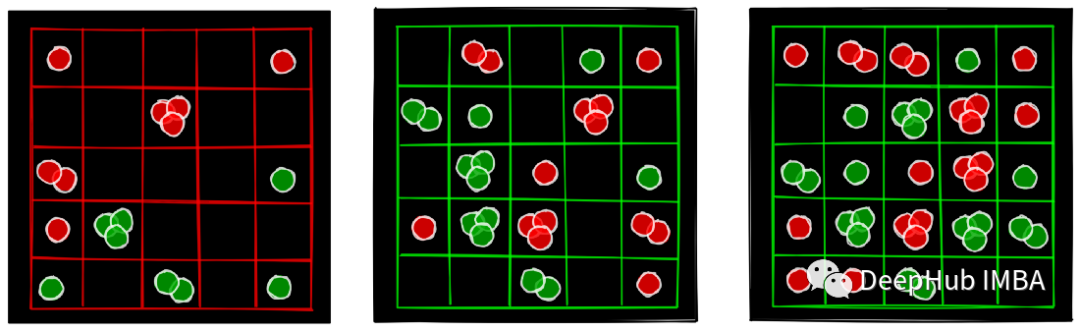
游戏板(简称黑板)上有M行N列,在上图中,M=N=5。黑板上有M*N = 25个单元格。在游戏开始时,所有的格子都是空的。
这些红色和绿色的圆形物体在游戏中被称为球体。下图显示了我们在游戏中可以拥有的球体(1个,2个或3个,红色或绿色)。
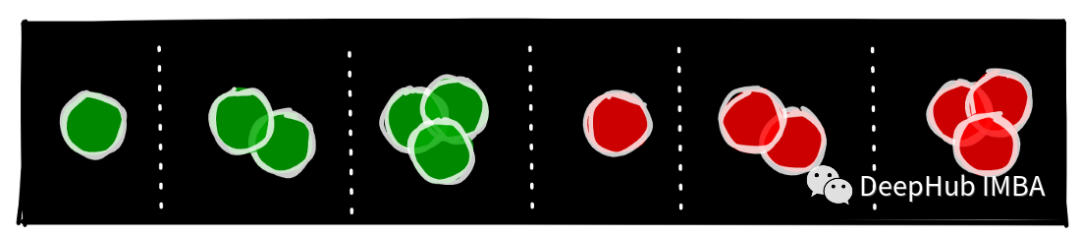
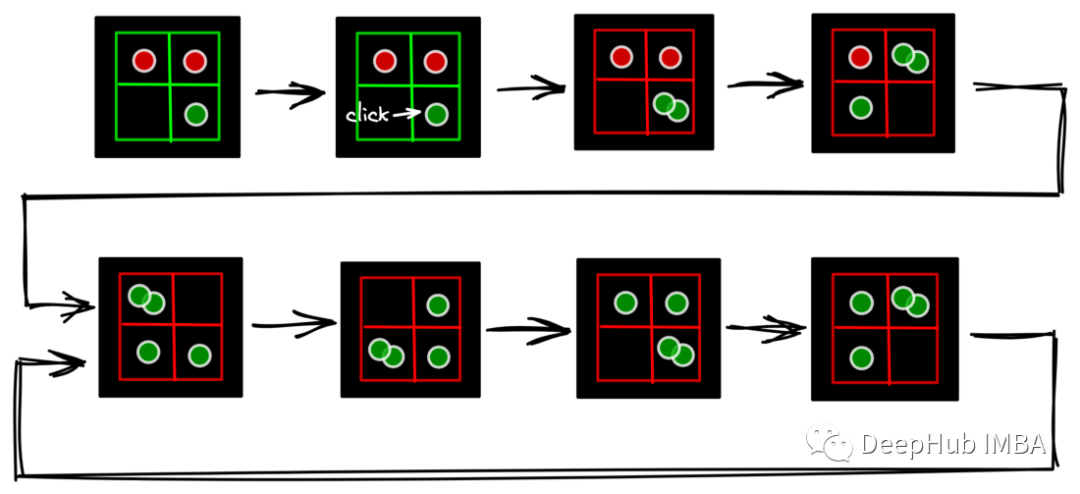
在一次操作中,玩家点击任何空的或颜色或玩家相同的单元格,它将增加该单元格中的球的数量。下面的动图展示了游戏中的一些动作。

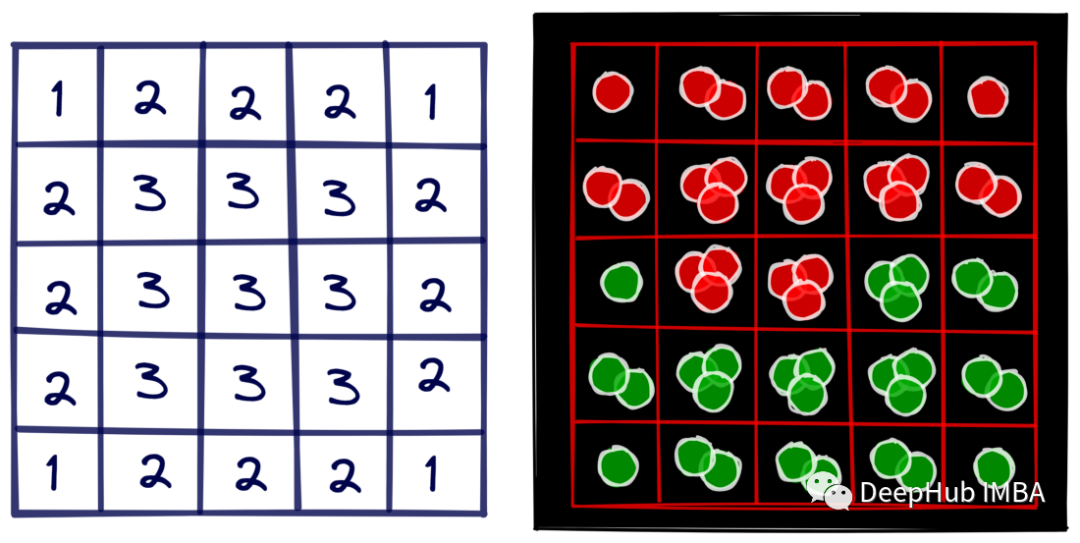
在一个特定的单元格中可以容纳多少个球是有限制的。一个单元格最多可以保存“该单元格的正交相邻邻居数-1”。对于中间的单元格,这个数字是3,对于边缘的单元格,这个数字是2,对于角落的单元格,这个数字是1。下图显示了5x5板中每个单元的最大球体数。
但当玩家点击一个已经拥有最多球体数量的单元格时会发生什么呢?那个单元格的球会分裂,把它所有的球推到邻近的单元格里。下面的动图显示了不同种类的球体的分割。

在分裂过程中,如果相邻单元格包含来自其他玩家的球,那么这些球的颜色将改变为当前玩家的颜色。如下图所示。

分裂后的单元格在其周围增加了球的数量,它可以导致进一步的多次分裂,开始分裂的连锁反应,这就是游戏名字的由来。单步操作后的连锁反应是这款游戏最终不可预测的原因。
现在我们知道了游戏是如何从一个状态发展到下一个状态的,可能会有分裂;或者在单个单元格中增加一个球体。但玩家如何获胜呢?游戏的目标很简单,玩家必须消灭棋盘上所有敌人的球。

游戏状态
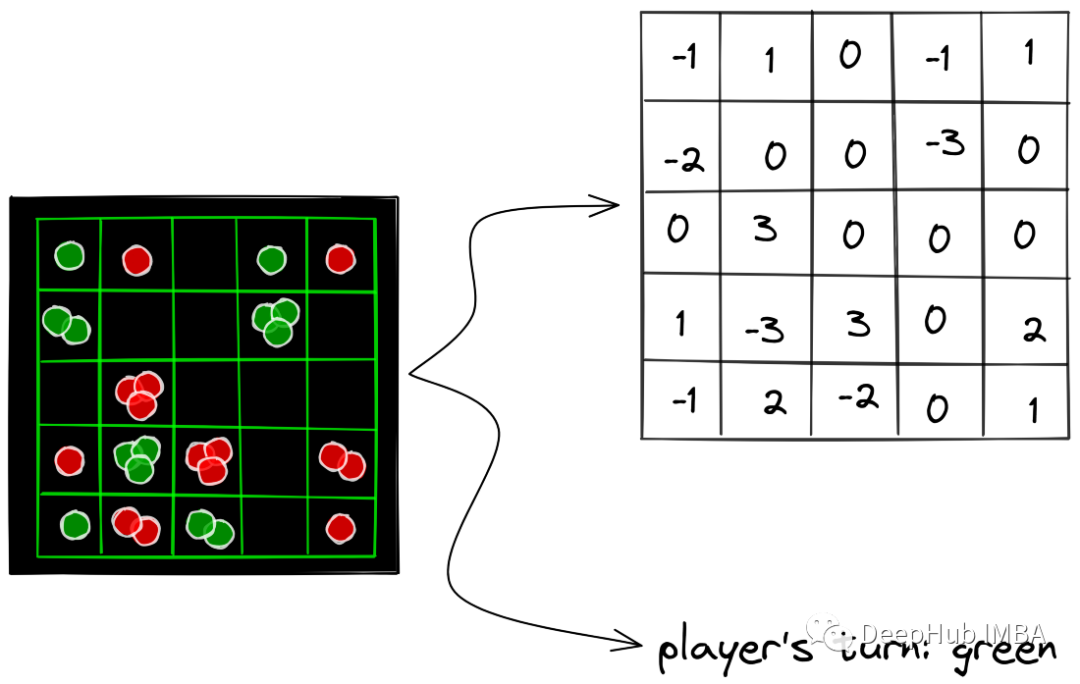
我们需要存储什么信息来捕捉游戏的状态呢?有两样东西——首先,一个M × N数组,它告诉我们棋盘上每个M*N格子中的球的数量和类型,其次,轮到谁“红”或“绿”。我们可以用正数来表示红色球的数量,用负数来表示绿色球的数量。下图显示了如何表示状态的示例。
状态转换
我们知道了如何表示一个状态,下面要关注一个更重要的问题,在当前状态下,如何得到下一个状态。为了获得下一个状态,需要知道玩家点击的单元格。我们称这个单元格为事件单元格。
将在事件单元格上做一些处理,它看起来像这样。我们将向它添加一个球体,并检查球体的数量是否超过单元格的限制。如果球的数量超过了,我们就需要把球分裂开。
在分裂的情况下,事件单元格的每个邻居都将获得一个球体,然后我们将处理这些邻居,依此类推。我们观察到,我们首先处理事件单元格,然后处理事件单元格的邻居,然后处理事件单元格邻居的邻居,依此类推。在某个级别i的邻居,可以以任何顺序处理;以任何顺序处理第I级上所有邻居的最终结果都是相同的。下图就是一个例子。
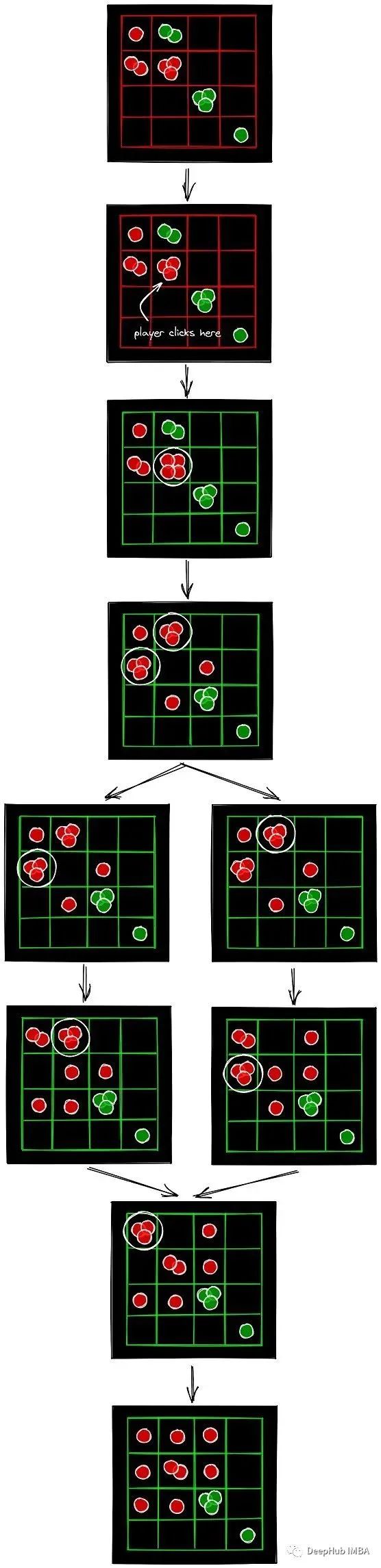
两种不同的方式处理同一级别的单元格都会得到相同的最终状态。第i层的处理顺序不重要的原因是,第i层有两种单元格,分裂的单元格和没有分裂的单元格。那些没有分裂的单元格的球数只会增加一个,不管处理顺序如何。那些分裂的单元格,只会给i+1级的单元格增加一个球体。也就是说,第i级和第i+1级的单元格集合总是不相交的,因此第i级所有单元格的相加之和对于第i+1级的每个单元格总是相同的。
所以本质上是在做广度优先遍历,这可以借助队列来实现状态转换。
实现简单的游戏规则
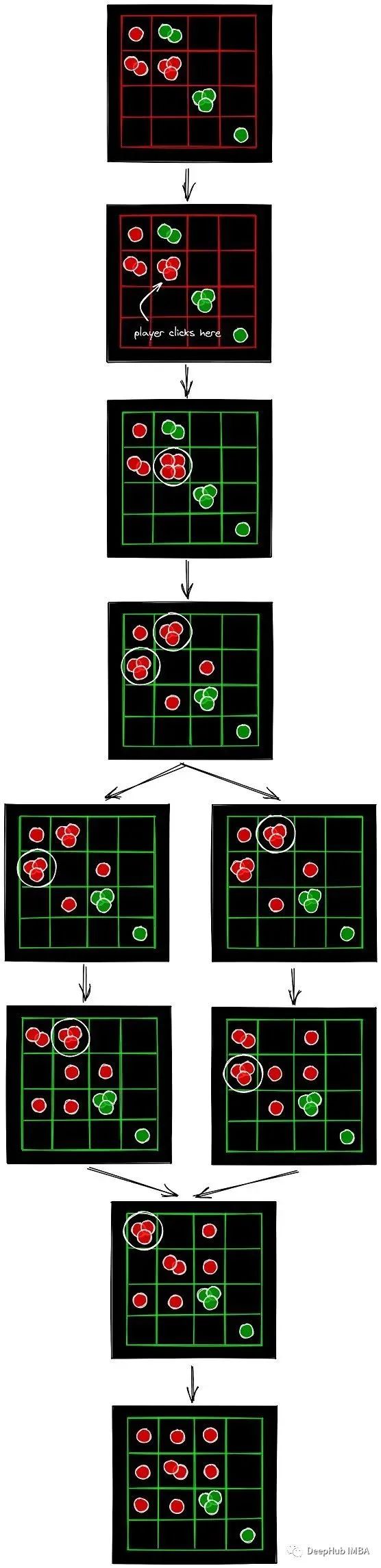
状态
实现状态表示并不复杂。将棋盘信息存储为不同numpy数组中的球的数量和球的颜色。状态表示还包括玩家的回合。
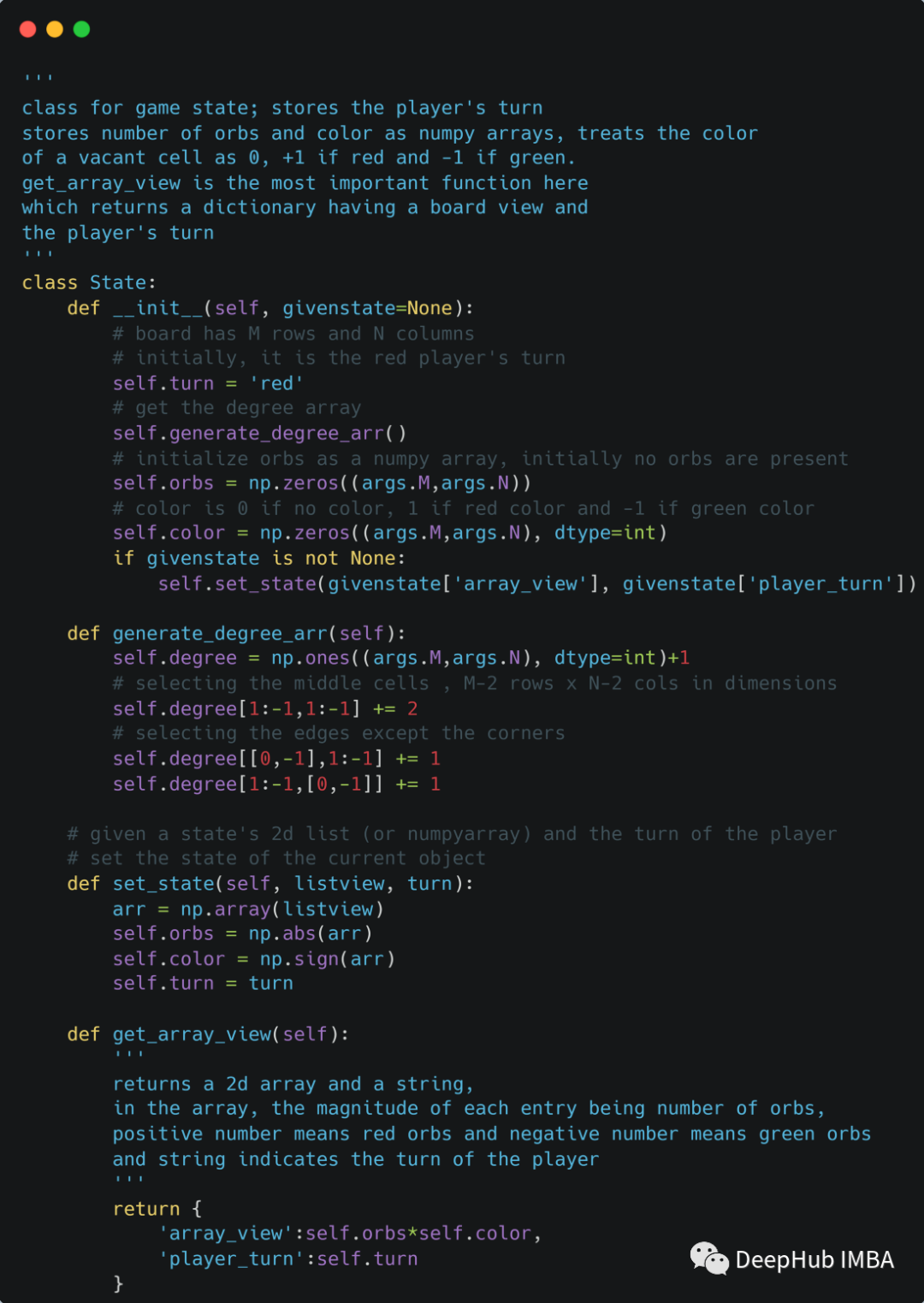
可视化
这些代码,分别使用矩形和圆绘制网格和球体。
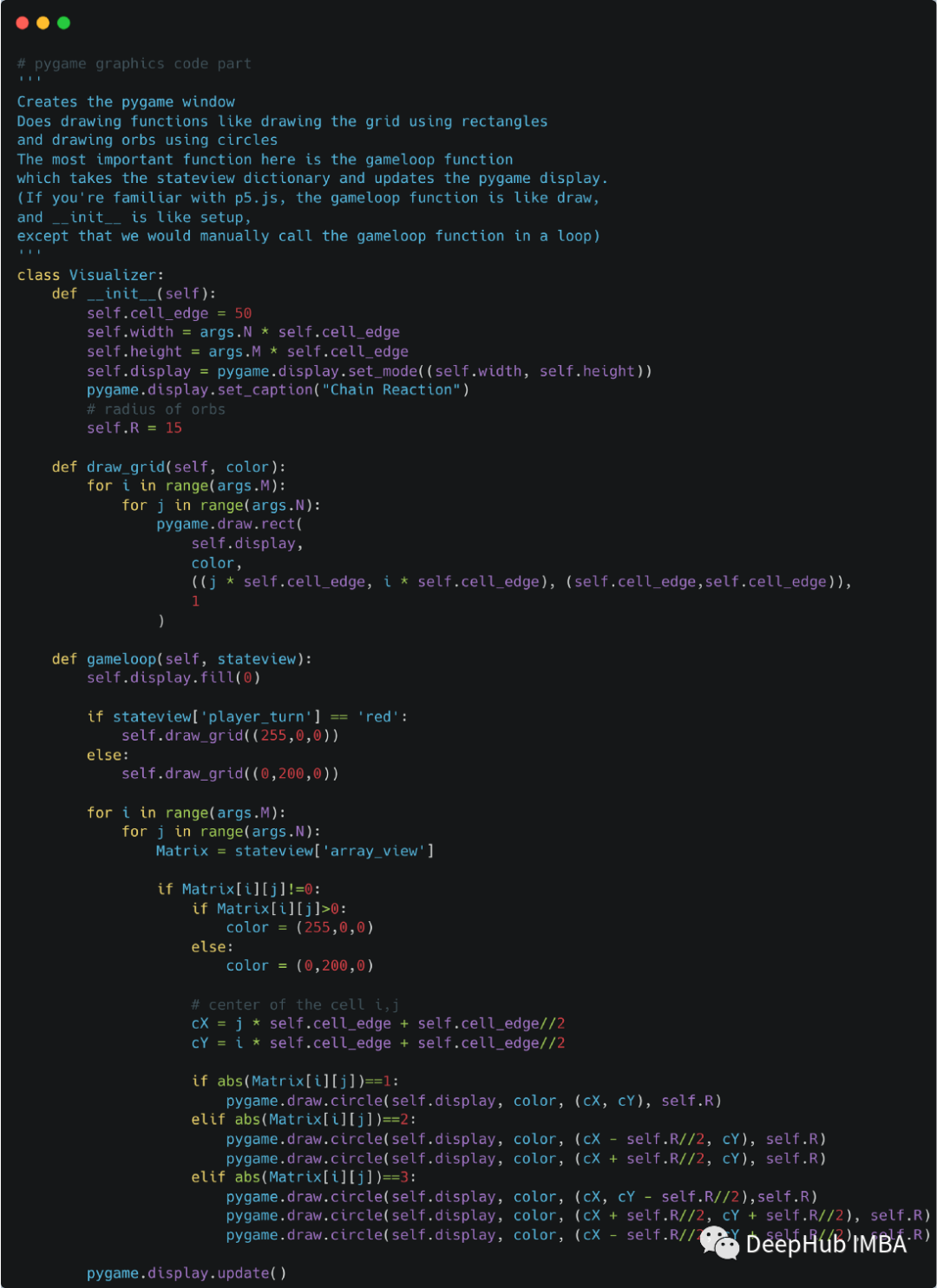
控制器
这里是最重要的代码段,即状态转换,即在给定当前状态和事件的情况下获得下一个状态。
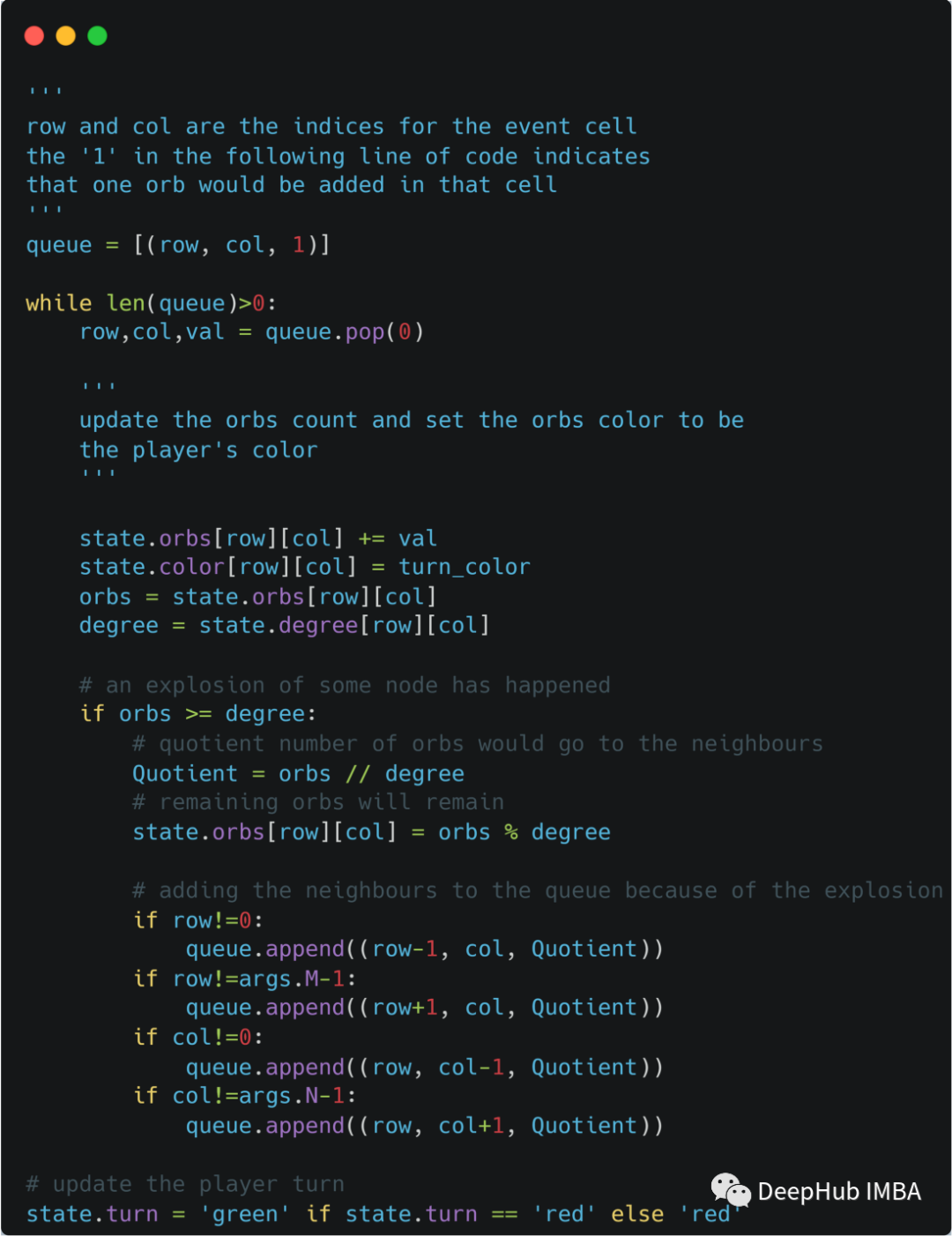
有一种情况是,球持续分裂,而其他玩家的球消失,如下图所示。
这里需要检查玩家是否在广度第一次遍历while循环中赢得了游戏。通过跟踪红色和绿色的球体计数(作为myorbs和opporbs)来检查它,并在循环的每次迭代中更新它们。

AlphaZero
AlphaZero到做了什么呢
[5]是理解AlphaZero的一个很好的起点。人类的推理有两种思维模式——一种是慢思维模式,一种是快思维模式。快速模式由直觉引导,而慢速模式像传统计算机算法一样明确遵循某些规则或步骤引导。
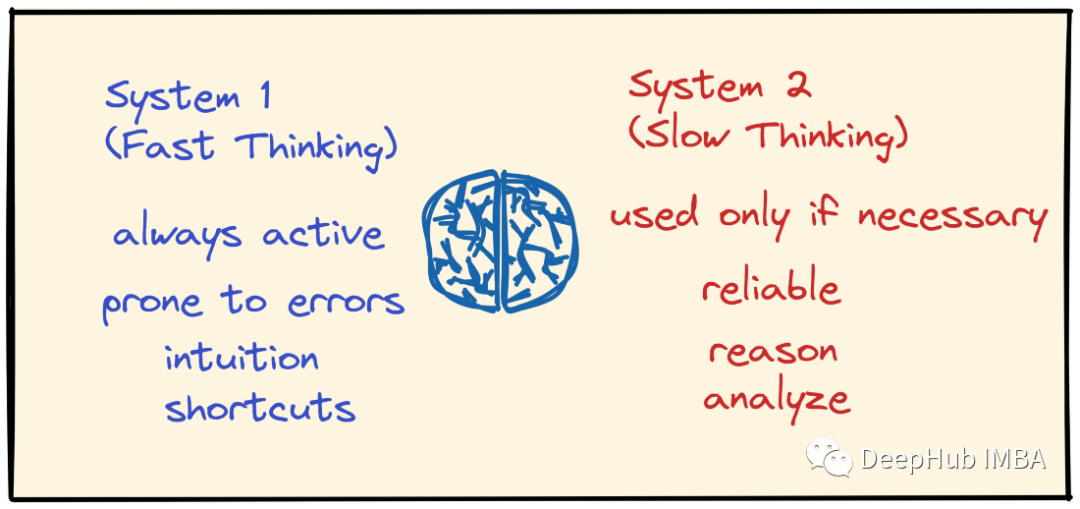
在AlphaZero中,快速模式或直觉都是通过一个神经网络实现的,该神经网络获取棋盘状态并输出一个策略(操作的概率分布)和一个值(告诉当前玩家给定棋盘状态有多好的分数);慢速思维模式则通过蒙特卡罗树搜索实现。
对于一个游戏我们可能会有一些自己的理解(经验),知道哪些行为更好,哪些不好。这种最初的理解可以表示为行为的概率分布。我们会将较高的概率分配给好的行动,而较低的概率分配给坏的行动(好的行动是那些能够带给我们胜利的行动)。如果我们没有这样的经验,那么我们可以从均匀概率分布开始。
这个操作上的概率分布就是我们对于给定状态的“策略”。
有一种方法可以改进这一原始政策——提前考虑未来可能采取的行动。从我们当前的状态出发,我们可以思考自己可以下什么棋,对手可以下什么棋等等。这种情况下我们实际上是在讨论树搜索,这种树搜索可以通过使用我们最初的理解来评估中间板的状态(获取值)来改进,并且可能不会花费大量的时间来探索具有低值的节点。在完成这个树搜索之后,将更好地了解在当前棋盘状态下玩什么,或者说我们得到了一个改进的策略。这整个过程被称为放大,这是AlphaZero使用蒙特卡洛树搜索完成的。
下一篇文章我们将详细介绍AlphaZero的一个简单实现。
References
[1] Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai, M., Guez, A., Lanctot, M., Sifre, L., Kumaran, D., Graepel, T., Lillicrap, T., Simonyan, K., & Hassabis, D. (2018). A general reinforcement learning algorithm that Masters Chess, Shogi, and go through self-play. Science, 362(6419), 1140–1144. https://doi.org/10.1126/science.aar6404
[2] https://brilliant.org/wiki/chain-reaction-game/
[3] Wu, D. J. [PDF] accelerating self-play learning in go: Semantic scholar. https://www.semanticscholar.org/paper/Accelerating-Self-Play-Learning-in-Go-Wu/f244ffb549a61806d00f614e70fa1c3fbe5fffc6
[4] https://medium.com/oracledevs/lessons-from-implementing-alphazero-7e36e9054191
[5] “How to Keep Improving When You’re Better Than Any Teacher — Iterated Distillation and Amplification.” YouTube, uploaded by Robert Miles, 3 Nov. 2019, https://www.youtube.com/watch?v=v9M2Ho9I9Qo.
[6] Anthony, T., Barber, D., & Tia, Z. Thinking fast and slow with deep learning and Tree Search. https://arxiv.org/pdf/1705.08439.pdf
作者:Bentou