支持向量机是1992年由Bell实验室的vladimir Vapnik和他的同事首次提出的。然而,许多人并不知道支持向量机的基础知识早在20世纪60年代他在莫斯科大学的博士论文中就已经开发出来了。几十年来,SVM一直受到很多人的青睐,因为它使用更少的计算资源,同时允许数据科学家获得显著的准确性。更不用说它同时解决了分类和回归问题。
基本概念
支持向量机可以解决线性和非线性问题,很好地工作在许多实际业务问题。支持向量机的原理是直截了当的。学习模型绘制了一条线,将数据点划分为多个类。在一个二元问题中,这个决策边界采用最宽的街道方法,最大限度地增加从每个类到最近的数据点的距离。
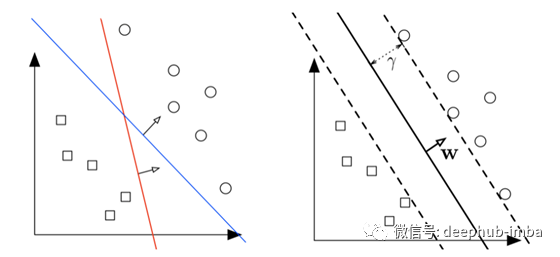
在向量微积分中,点积可测量一个向量在另一个向量上的“数量”,并告诉您在位移方向或另一个向量方向上的作用力大小。
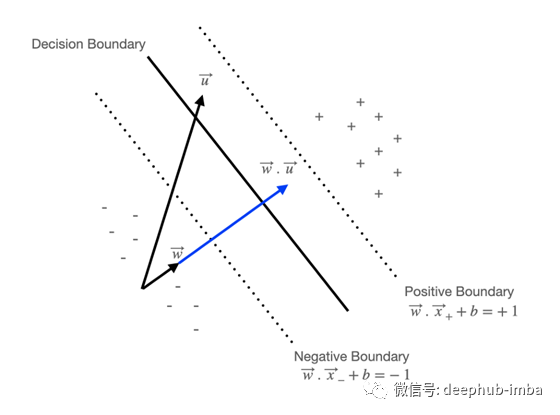
例如,我们有未知向量u和垂直于决策边界的法向向量w。w·u的点积表示u在矢量w方向上所经过的力的大小。在这方面,如果未知向量u位于边界的正侧,则可以用常数b如下所述。
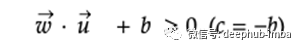
可以相应地表示位于对正样本进行分类(+1)的边界上方或对负样本进行分类(-1)的边界下方的样本。

决策规则
确定决策边界后,应以使每个组中最接近的样本最大化宽度的方式绘制正边界和负边界,并将这些样本放置在每个组的边界上。
此规则将成为查找最大边界宽度的约束。假设y对正样本为+1,对负样本为-1,则上述两个等式都可以通过在等式两边乘以y来在正边界或负边界线上表示样本x。它们也称为支持向量。
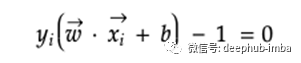
决策规则-最大宽度
假设我们在正边界线上有矢量x +,在负边界线上有矢量x-。x +负x-表示从负矢量x-到正矢量x +的方向力。如果我们在这个方向力上以垂直于决策边界的单位矢量w进行点积运算,则这将成为负边界与正边界之间的宽度。注意w是法线向量,|| w || 是w的大小。
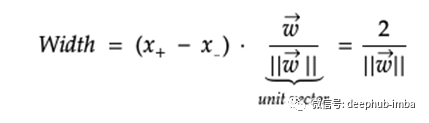
我们基本上将此宽度最大化,以将负数据点和正数据点区别开来。可以简化如下。为了数学上的方便,最后一种形式将w的大小平方并除以2。
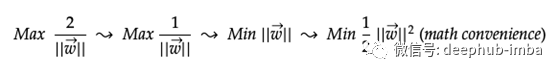
查找有约束的最大宽度
拉格朗日方程可用于求解约束优化问题。如果约束变化一个单位,则目标函数的最大值将减少λ。在给定约束的情况下,该方程式通常用于查找目标函数的最大值或最小值。
- L(x,λ)= f(x)-λg(x)
- f(x):目标函数
- g(x):约束
- λ:拉格朗日常数
前面我们提到过,SVM采用最宽的街道方法来找到正边界和负边界之间的最大宽度。可以使用目标函数和约束定义如下的拉格朗日方程来描述此问题。
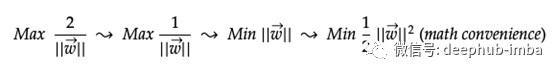
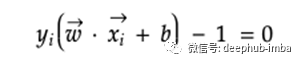
总之,考虑到样本是分界线上的支持向量,拉格朗日最小化了目标函数(最终最大化了正边界和负边界之间的宽度)。
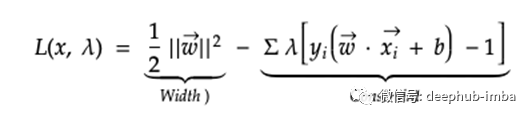
从上式中找到关于w和b的导数后,可以简化如下。由于y i和y j是标签或响应变量,可以通过最大化向量x i和x j的点积来简单地使方程最小化。换句话说,宽度的最大化全部取决于绘制边界线时对支撑向量对的点积求和。
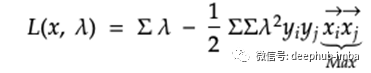
此外,根据支持向量x和u的点积,确定未知向量u是否位于决策边界的正侧。
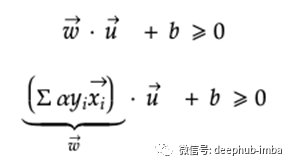
内核技巧
在线性问题中,SVM可以轻松地绘制决策边界,以将样本分为多个类别。但是,如果无法用线性切片将数据点分开,则可以在绘制决策边界之前对数据点进行转换,这称为“内核技巧”。
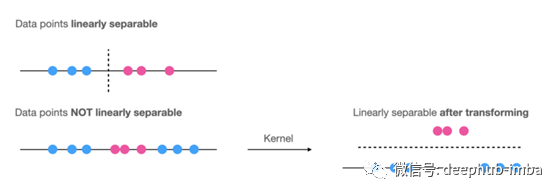
非线性SVM在使用内核技巧变换后变成了线性SVM问题。通过使用称为内核的特殊函数进行非线性变换,内核基本上将问题从输入空间映射到新的高维空间(称为特征空间))(x)。然后,使用线性模型来分离特征空间中的数据点。特征空间中的线性模型对应于输入空间中的非线性模型。
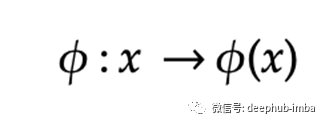
SVM基本规则可以在特征空间中表示如下。下面的等式是用w,y和x的线性总和代替w的大小。 使用内核的好处在于原始方程式不会改变,因为内核转换是在phi中抽象的。
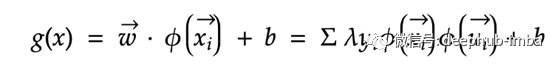
这是内核功能的示例。一般情况下可以从最简单的转换版本开始,然后逐步使用越来越高级的内核功能进行建模,以避免过度拟合。

作者:Yohan Chung
原文地址:https://medium.com/analytics-vidhya/support-vector-machines-math-explained-d48c4edb3d4e
deephub翻译组