谱聚类和AP聚类是基于图的两种聚类,在这里我介绍AP聚类。
Affinity Propagation Clustering(简称AP算法)是2007提出的,当时发表在Science上《single-exemplar-based》。特别适合高维、多类数据快速聚类,相比传统的聚类算法,该算法算是比较新的,从聚类性能和效率方面都有大幅度的提升。
Affinity Propagation可以翻译为关联传播,它是一种基于数据点之间“消息传递”概念的聚类技术,所以我们称其为基于图的聚类方法。
该算法通过在数据点之间发送消息直到收敛来创建簇。它以数据点之间的相似性作为输入,并根据一定的标准确定范例。在数据点之间交换消息,直到获得一组高质量的范例。与k-means或k-medoids等聚类算法不同,传播在运行算法之前不需要确定或估计簇的数量。
公式详解
我们使用下面的数据集,来介绍算法的工作原理。
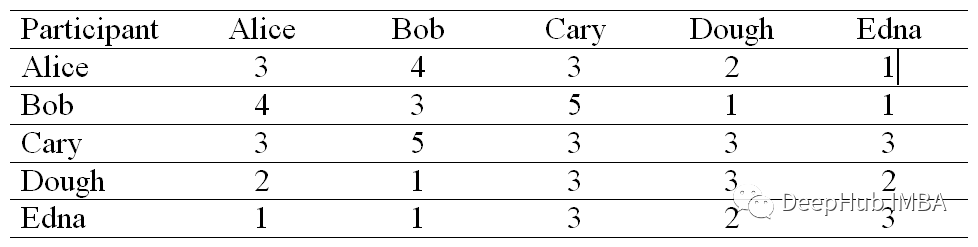
相似矩阵
相似度矩阵中的每一个单元格都是通过对参与者之间的差值平方和求负来计算的。
比如 Alice 和 Bob 的相似度,差的平方和为 (3–4)² + (4–3)² + (3–5)² + (2–1)² + (1– 1)² = 7。因此,Alice 和 Bob 的相似度值为 -(7)。
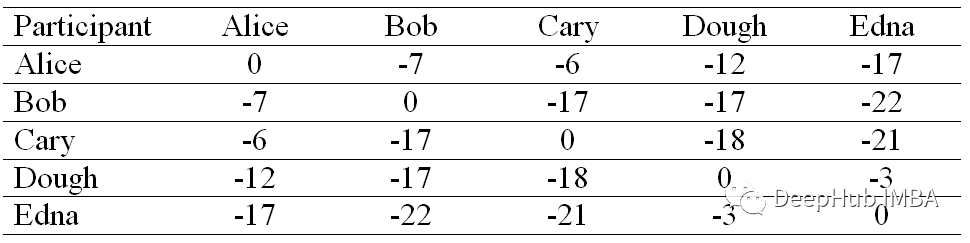
如果为对角线选择较小的值,则该算法将围绕少量集群收敛,反之亦然。因此我们用 -22 填充相似矩阵的对角元素,这是我们相似矩阵中的最小值。
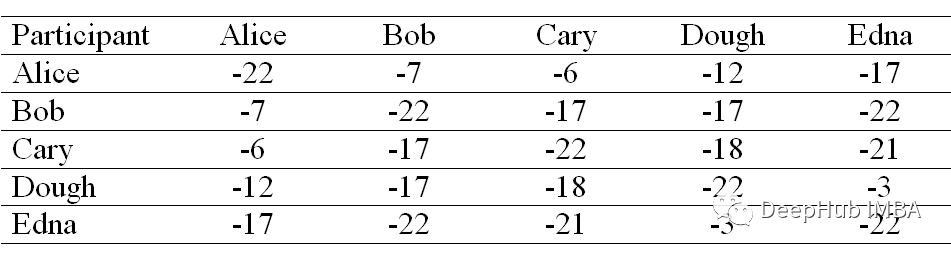
吸引度(Responsibility)矩阵
我们将首先构造一个所有元素都设为0的可用性矩阵。然后,我们将使用以下公式计算吸引度矩阵中的每个单元格:
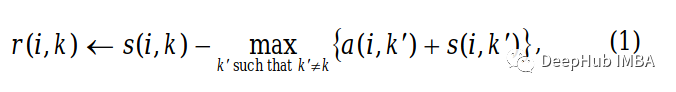
这里i指的是行,k指的是相关矩阵的列。
例如,Bob(列)对Alice(行)的吸引度是-1,这是通过从Bob和Alice的相似度(-7)中减去Alice所在行的最大相似度(Bob和Alice的相似度(-6)除外)来计算的。

在计算了其他参与者对的吸引度之后,我们得到了下面的矩阵。
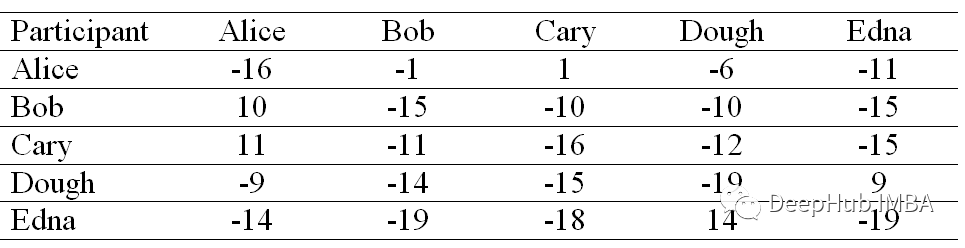
吸引度是用来描述点k适合作为数据点i的聚类中心的程度。
归属度(Availability)矩阵
为了构造一个归属度矩阵,将使用对角和非对角元素的两个单独的方程进行计算,并将它们应用到我们的吸引度矩阵中。
对角线元素将使用下面的公式。
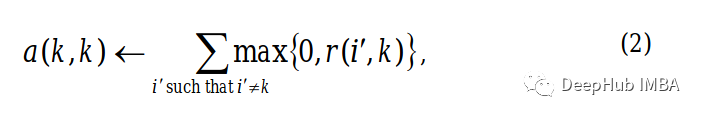
这里 i 指的是关联矩阵的行和 k 列。
该等式告诉我们沿列计算所有大于 0 的值的总和,但值等于所讨论列的行除外。例如,Alice 的对角线上元素值将是 Alice 列的正值之和,但不包括 Alice 列的值,等于 21(10 + 11 + 0 + 0)。
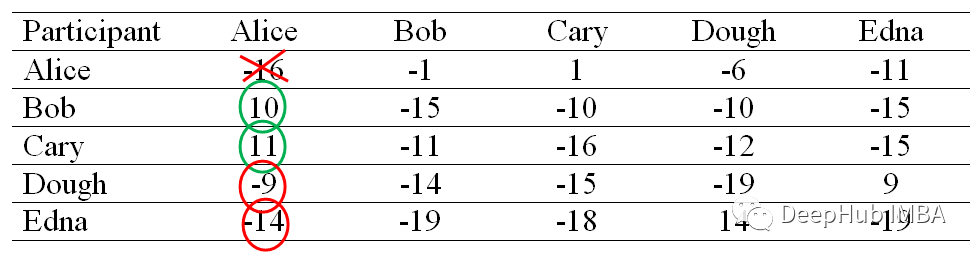
修改后,我们的归属度矩阵将如下所示:

现在对于非对角元素,使用以下等式更新它们的值。
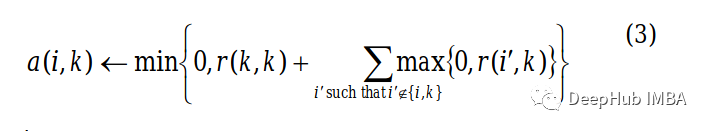
通过一个例子来理解上面的等式。假设我们需要找到 Bob(列)对 Alice(行)的归属度,那么它将是 Bob 的自我归属(在对角线上)和 Bob 列的剩余积极吸引度的总和,不包括 Bob 的Alice行(-15 + 0 + 0 + 0 = -15)。
在计算其余部分后,得到以下归属度矩阵。
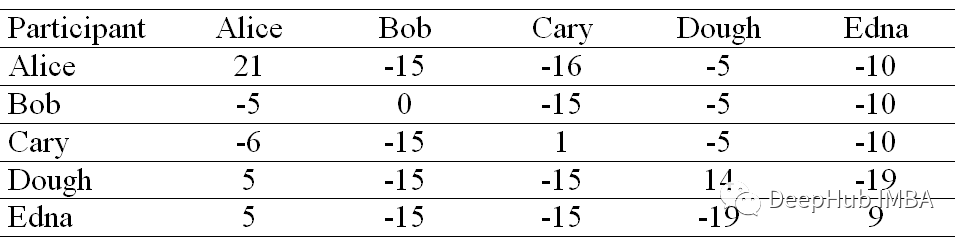
归属度可以理解为用来描述点i选择点k作为其聚类中心的适合程度。
准据(Criterion)矩阵
准据矩阵中的每个单元格只是该位置的吸引度矩阵和归属度矩阵相加的和。
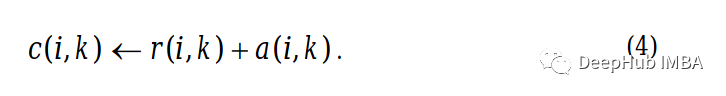
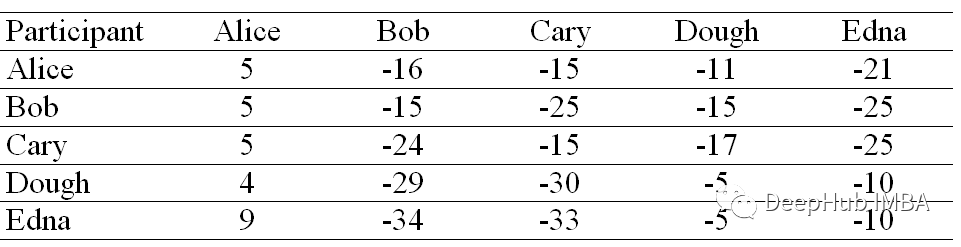
每行中具有最高准据值的列被指定为样本。共享同一个实例的行在同一个簇中。在我们的示例中。Alice、Bob、Cary 、Doug 和 Edna 都属于同一个集群。
如果情况是这样:
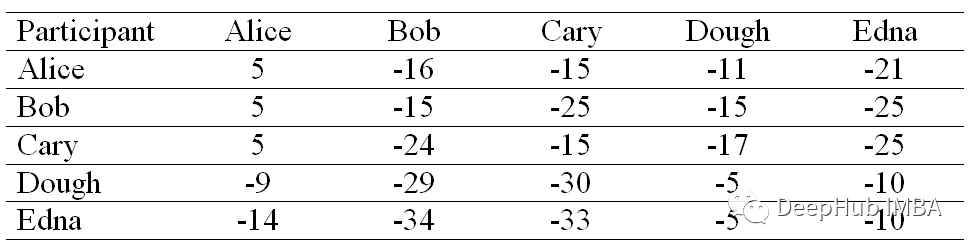
那么Alice、Bob 和 Cary 构成一个簇,而 Doug 和 Edna 构成第二个簇。
Criterion被我翻译成准据也就是说明这个矩阵是我们聚类算法判断的标准和依据。
代码示例
在sklearn中已经包含了该算法,所以我们可以拿来直接使用:
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
sns.set()
from sklearn.datasets import make_blobs
from sklearn.cluster import AffinityPropagation
从 Sklearn 生成聚类数据
X, clusters = make_blobs(n_samples=1000, centers=5, cluster_std=0.8, random_state=0)
plt.scatter(X[:,0], X[:,1], alpha=0.7, edgecolors='b')
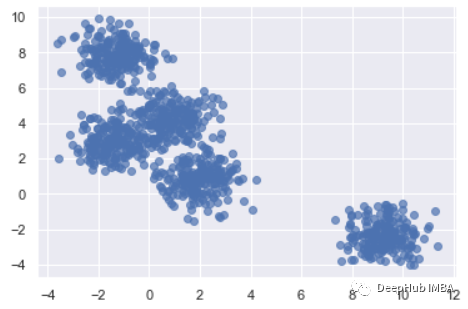
初始化和拟合模型。
af = AffinityPropagation(preference=-50)
clustering = af.fit(X)
AP聚类应用中需要手动指定Preference和Damping factor,虽然不需要显式指定簇的数量,但是这两个参数其实是原有的聚类“数量”控制的变体:
Preference:数据点i的参考度称为p(i)或s(i,i),是指点i作为聚类中心的参考度,聚类的数量受到参考度p的影响,如果认为每个数据点都有可能作为聚类中心,那么p就应取相同的值。如果取输入的相似度的均值作为p的值,得到聚类数量是中等的。如果取最小值,得到类数较少的聚类。
Damping factor(阻尼系数):主要是起收敛作用的。
绘制聚类结果的数据点
plt.scatter(X[:,0], X[:,1], c=clustering.labels_, cmap='rainbow', alpha=0.7, edgecolors='b')
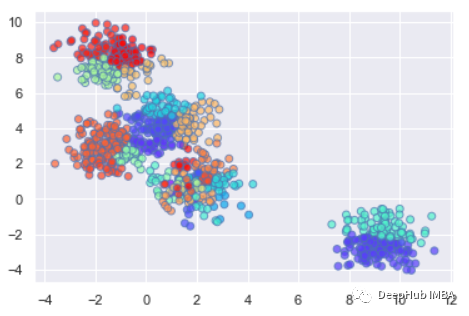
总结
Affinity Propagation 是一种无监督机器学习技术,特别适用于我们不知道最佳集群数量的情况。并且该算法复杂度较高,所以运行时间相对比K-Means长很多,这会使得尤其在海量数据下运行时耗费的时间很多。
作者:Sarthak Kedia