一不小心就弄懂了 冒泡，选择，插入，希尔,归并和快速排序

今天我们主要看一些简单的排序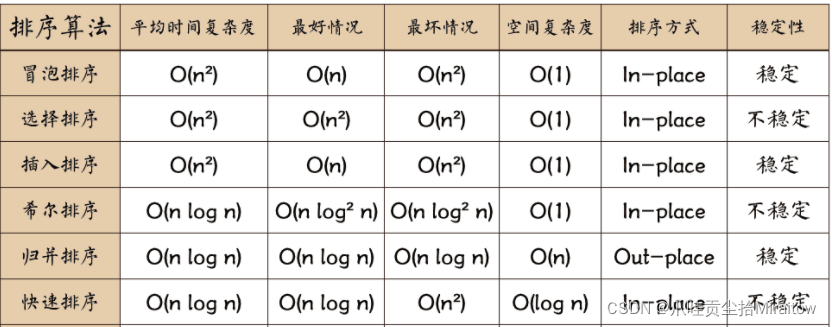

常见的时间复杂度

🎈 常数阶Ο(1)
🎈 对数阶Ο(log2n)
🎈 线性阶Ο(n)
🎈 线性对数阶Ο(nlog2n)
🎈 平方阶Ο(n²)
🎈 立方阶Ο(n³)
🎈 K次方阶Ο(n^k)
🎈 指数阶Ο(2^n)

常见的时间复杂度对应图

Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n²)＜Ο(n³)＜…＜Ο(2^n)
＜Ο(n!)<O(n^n)

💓 冒泡排序（Quicksort）

算法描述：

①. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
②. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
③. 针对所有的元素重复以上的步骤，除了最后一个。
④. 持续每次对越来越少的元素重复上面的步骤①~③，直到没有任何一对数字需要比较。

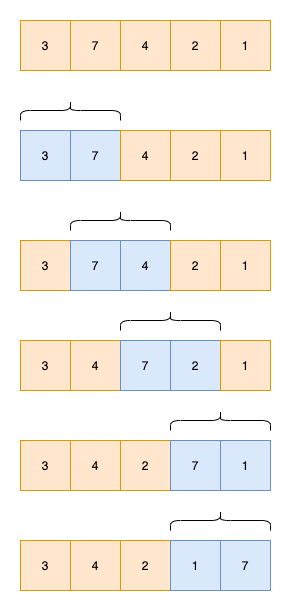
为了直观感受，在网上找个动态的演示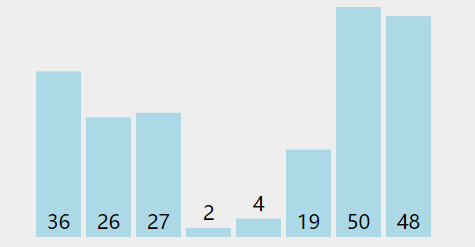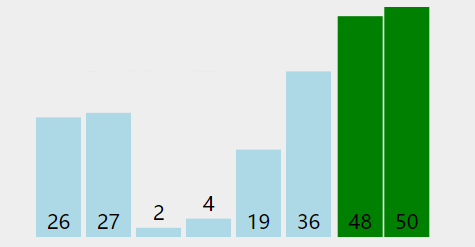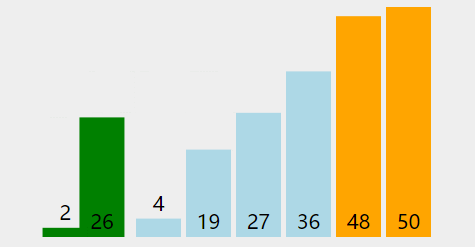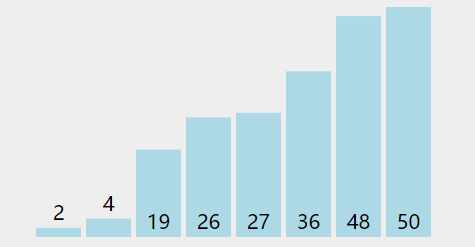

代码实现：

当数组中有n个元素时，只需要进行n-1轮比较，则整个数组就是有序的
publicstaticvoidbubbleSort(int[] arr){// 进行i轮比较for(int i =0; i < arr.length -1; i++){for(int j =0; j < arr.length -1- i; j++){//后一位的值大于前一位的值进行值交换if(arr[j]> arr[j +1]){swap(arr, j, j +1);}}}}publicstaticvoidswap(int[] arr,int i,int j){int temp = arr[i];
    arr[i]= arr[j];
    arr[j]= temp;}

🧡 选择排序（Quicksort）

算法描述：

选择排序是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，继续放在起始位置知道未排序元素个数为0。

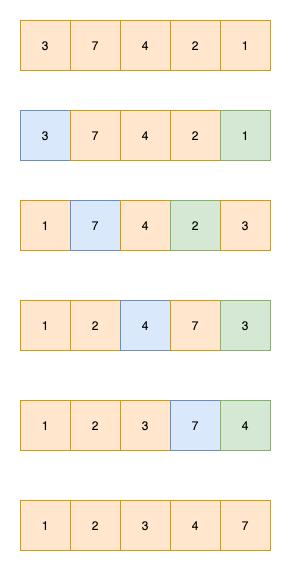
代码实现：

publicstaticvoidselectionSort(int[] a){//每当完成一轮，将会找到最小值，一个i代表一轮for(int i =0; i < a.length; i++){int index = i;//每一轮从i+1开始找，查找是否有比当前值更小的值for(int j = i +1; j < a.length; j++){if(a[index]> a[j]){
                index = j;}}//如果index和i不相等说明，下标交换过，也就是说找到更小的数值了if(index != i){swap(a, index, i);}}}publicstaticvoidswap(int[] a,int i,int j){int temp = a[i];
    a[i]= a[j];
    a[j]= temp;}

💛 插入排序（insertSort）

算法描述：

插入排序也是一种常见的排序算法，插入排序的思想是：将初始数据分为有序部分和无序部分，每一步将一个无序部分的数据插入到前面已经排好序的有序部分中，直到插完所有元素为止。
插入排序的步骤如下：每次从无序部分中取出一个元素，与有序部分中的元素从后向前依次进行比较，并找到合适的位置，将该元素插到有序组当中。
将数组分为2端，有序数组和无序数组，依次将无序数组中的值插入到无序数组中。

如图，插入4的过程如下
将数组分为2端，有序数组和无序数组，依次将无序数组中的值插入到无序数组中。

如下图3 6 7为有序数组，4 2为无序数组。依次将4，2插入到无序数组中即可

如图，插入4的过程如下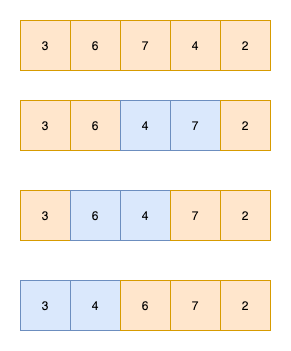

代码实现：

publicstaticvoidinsertionSort(int[] a){for(int i =1; i < a.length; i++){int temp = a[i];int j;// 查到合适的插入位置，插入即可for(j = i -1; j >=0&& a[j]> temp; j--){
            a[j +1]= a[j];}
        a[j +1]= temp;}}

💚 希尔排序 （ShellSort）

算法描述：

希尔排序是基于插入排序改进后的算法。因为当数据移动次数太多时会导致效率低下。所以我们可以先让数组整体有序（刚开始移动的幅度大一点，后面再小一点），这样移动的次数就会降低，进而提高效率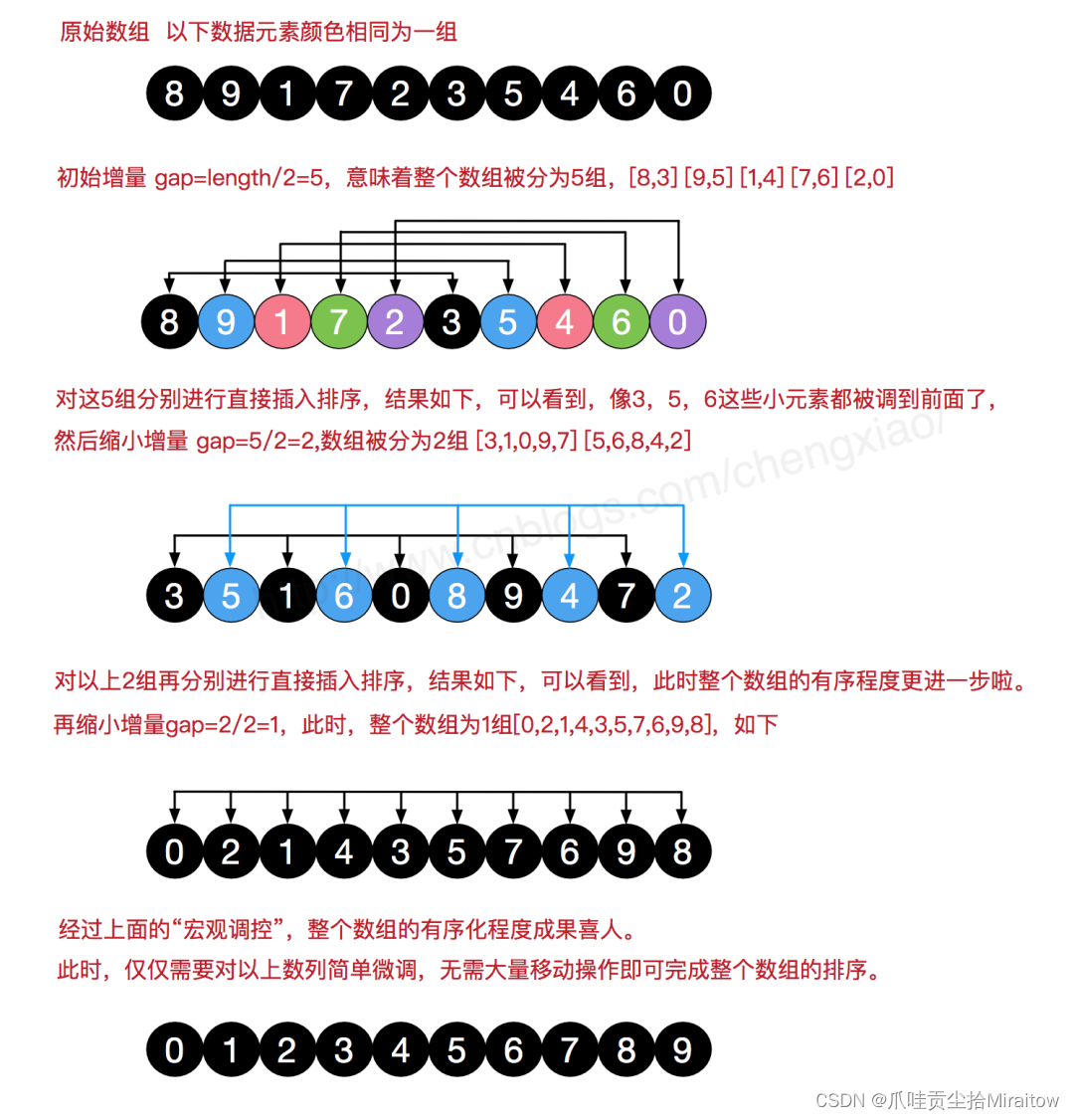

代码实现：

publicstaticvoidshellSort(int[] a){for(int step = a.length /2; step >0; step /=2){//接下来的过程类似于插入排序for(int i = step; i < a.length; i++){int temp = a[i];int j;for(j = i - step; j >=0&& a[j]> temp ; j -= step){
                a[j + step]= a[j];}
            a[j + step]= temp;}}}

💙 归并排序（MergetSort）

算法描述：

1.申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

2.设定两个指针，最初位置分别为两个已经排序序列的起始位置；

3.比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

4.重复步骤 3 直到某一指针达到序列尾；

将另一序列剩下的所有元素直接复制到合并序列尾。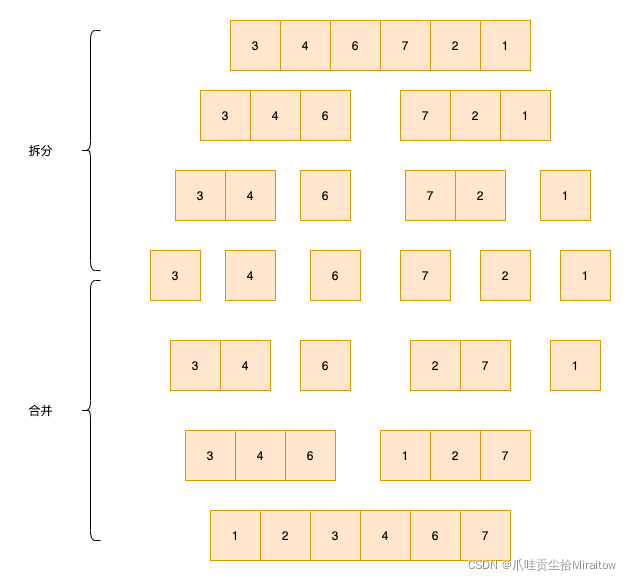

方便理解，直接网上找图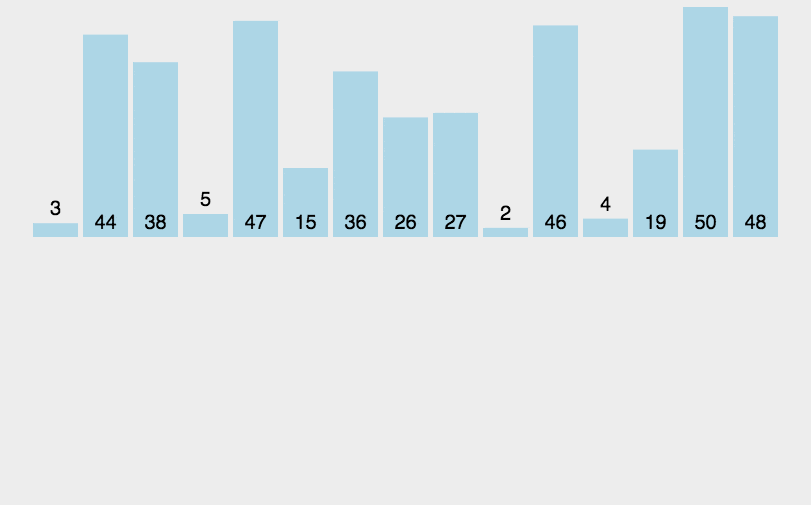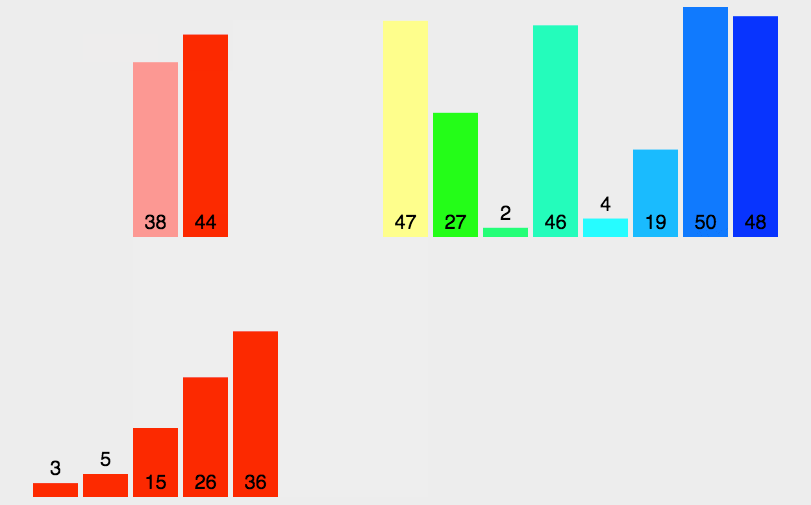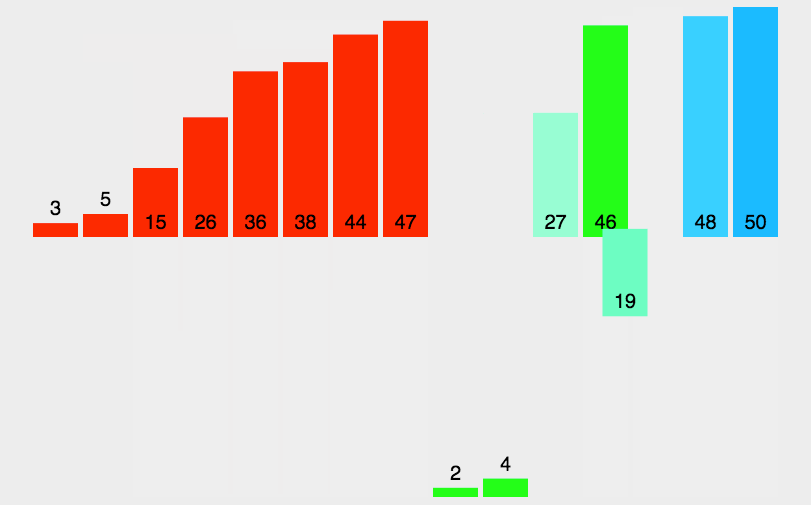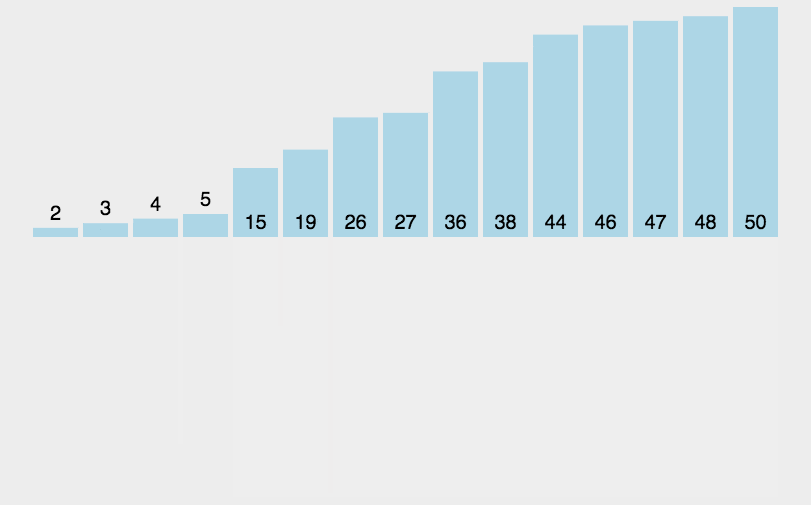

代码实现：

publicstaticvoidmergeSort(int[] a,int left,int right){// 将数组分段成只有一个元素if(left == right){return;}int mid =(left + right)/2;mergeSort(a, left, mid);//递归mergeSort(a, mid +1, right);merge(a, left, mid, right);}publicstaticvoidmerge(int[] a,int left,int mid,int right){int[] temp =newint[right - left +1];int i = left;int j = mid +1;int k =0;while(i <= mid && j <= right){if(a[i]< a[j]){
            temp[k++]= a[i++];}else{
            temp[k++]= a[j++];}}// 复制左边数组剩余的值while(i <= mid){
        temp[k++]= a[i++];}// 复制右边数组剩余的值while(j <= right){
        temp[k++]= a[j++];}int index =0;//把temp全部复制给数组while(left <= right){
        a[left++]= temp[index++];}}

💜 快速排序（QuickSort）

算法描述：

1. 快速排序的执行流程主要分为如下三步
2. 从数列中取出一个数作为基准数
3. 分区，将比它大的数全放到它的右边，小于或等于它的数全放到它的左边
4. 再对左右区间重复第二步，直到各区间只有一个数

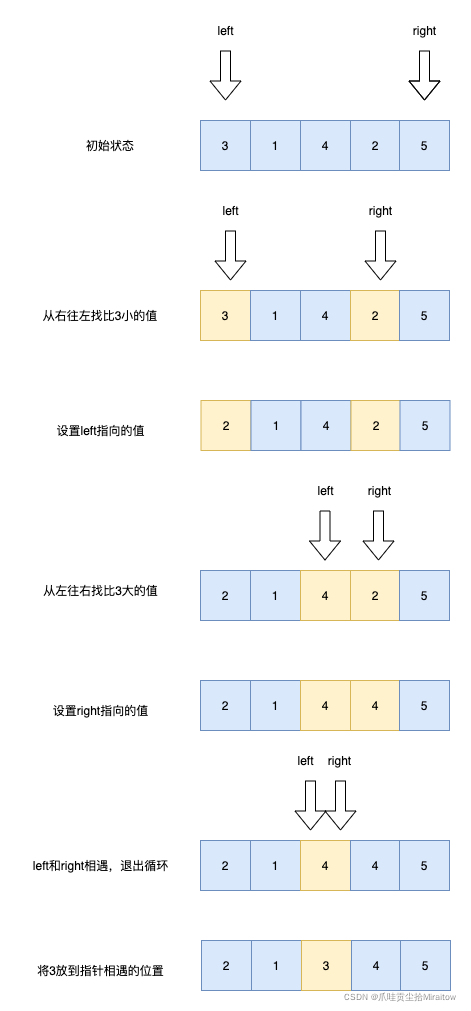
代码实现：

publicstaticvoidquickSort(int[] a,int left,int right){if(left >= right){return;}int index =sort(a, left, right);//得到中间值index，然后一分为二，继续分quickSort(a, left, index -1);quickSort(a, index +1, right);}publicstaticintsort(int[] a,int left,int right){//以左边的a[left]为基准数int key = a[left];while(left < right){// 从right所指位置向前搜索找到第一个关键字小于key的记录和key互相交换while(left < right && a[right]>= key){
            right--;}
        a[left]= a[right];// 从left所指位置向后搜索，找到第一个关键字大于key的记录和key互相交换while(left < right && a[left]<= key){
            left++;}
        a[right]= a[left];}// 放key值，此时left和right相同
    a[left]= key;return left;}