Ubuntu篇Crypto常见工具

前言

在Ubuntu实践Github上几种热门的密码学工具，帮助CTFer有效实战。

Ubuntu

本文Ubuntu版本22.04，默认python版本3.10，自带openssl

Ubuntu22.04多个python版本切换

某些工具，比如ciphey，不能在python3.10上使用，所以需要在ubuntu内置多个python版本切换使用。

本文采用annaconda来管理python版本。

#创建虚拟环境,envx.x(虚拟环境名称)
conda create -n envx.x python=X.X（3.6、3.7等）

'''
如出现 WARNING: A newer version of conda exists.
则输入以下命令
conda clean --packages --tarballs   #清除conda
conda update --all                  #更新conda
创建过程中出现 Proceed ([y]/n)?
即：是否确认将默认环境的包导入进虚拟环境中
'''

#激活虚拟环境
source activate envx.x

#退出虚拟环境
source deactivate envx.x

#删除虚拟环境
conda remove -n envx.x --all

#查看安装了哪些包
conda list

'''
可以在已激活的虚拟环境中安装一个包并查看，退出环境后，
再次查看默认环境的包，自行对比确认虚拟环境创建完成
'''

#查看当前存在哪些虚拟环境
conda env list 

Sagemath

Sage基于并使用Python，Python程序可以在Sage中直接运行，也可以在Sage中使用Python的各种库。sage是Crypto学习者的利器。

安装

打开software即可安装。

但这里还是有换源的问题。

笔者这里因为网速还ok，一直用的官方自带cn源。

在这里换源尝试一下

sudo apt update
sudo apt upgrade

即可安装成功

①

在Ubuntu里打开后会自动在本地搭建一个Jupyter Notebook，自动弹出浏览器访问，本地访问对应的url。

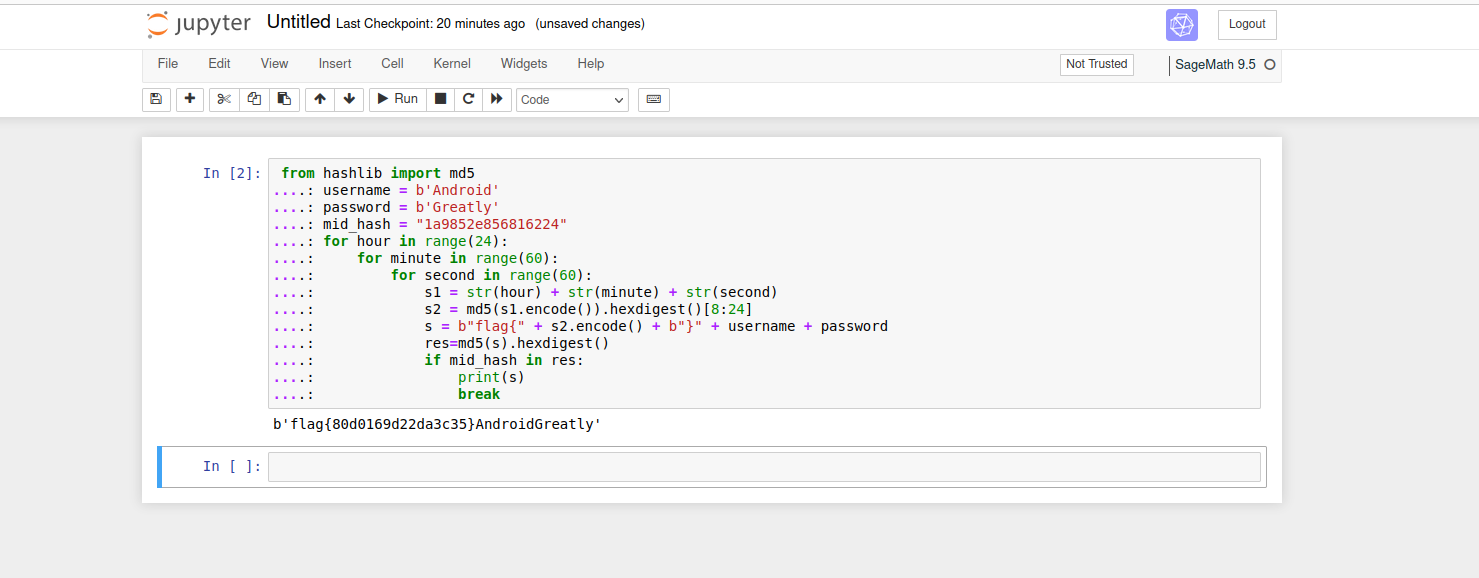
可以直接打开对应sage或者python脚本进行编辑，但是不能运行。可以new一个python3或者sage的notebook来编写、调试、运行代码。

也可以在此处下载包。

②

在terminal运行脚本

sage xxx.py

③

将sage导入python脚本

可以在Python脚本中将Sage作为库导入。

注意：需要使用与Sage捆绑的Python版本（当前为python3.10.6）运行该Python脚本。要导入Sage，需要在Python脚本中添加以下内容：

**from****sage.all****import** *

若想运行脚本，

如②中

**python hi.sage.py**

运行报错，但

**python hi.sage**

可以运行

# This file was *autogenerated* from the file hi.sage
from sage.all_cmdline import *   # import sage library

print('hi')

需要使用该选项调用Sage -python 它将使用Sage附带的Python版本运行脚本。

例如，如果Sage在你的 PATH 变量，则可以执行以下操作：

sage -python /path/to/my/script.py

另一种方法是编写Sage脚本并使用Sage本身运行该脚本。Sage脚本具有文件扩展名 .sage 和或多或少是一个Python脚本，但使用Sage特定的函数和命令。然后可以运行Sage脚本，如下所示：

sage /path/to/my/script.sage

这将负责加载必要的环境变量和默认导入。

Ciphey

自动化大量解密和解码的工具，例如多个基本编码，经典密码，哈希或更高级的加密，同时也支持自定义算法。据说比cyberchef更强。

日常在CTF中，偶尔会碰到一些不能一眼看出编码规则的字符串，这些字符串的编码规则或许并不复杂，但由于有限的知识面和脑洞并不能马上解码，严重影响效率。

安装过程中需要注意此工具对python版本的要求。

安装完成后，开箱即用

1.文件输入ciphey -f encrypted.txt
2.非限定输入ciphey -- "Encrypted input"
3.正常方式ciphey -t "Encrypted input"

例1：ctfshow crypto12

例2：ctfshow新手杯 easy_base

本例虽然不能给到完整的正确flag，但可以快速给到大致的flag样式来给选手提供思路。

实际上把TZ改为64即可提交flag。

最简洁路径：reverse—base64—flag

例3：base91+base32加密

CTF-RSA-tool

前提：需要安装python2.7

一款基于python以及sage的小工具，助不熟悉RSA的CTFer在CTF比赛中快速解决RSA相关的基本题型。

安装完成后，

python solve.py -h

符号链接

如不在项目目录下打开，可以做个符号链接，链接solve.py到bin目录下

ln -s /home/y/Desktop/CTF-RSA-tool/solve.py /usr/local/bin/rsa_solve

之后，就能直接在终端输入

rsa_solve -i rsa.txt

去快速秒简单题了

rsa.txt的编写规范参看

examples/input_example.txt

一行一个变量，可以写做 n = *** 或者 n is *** 或者 n : ***
识别的变量名有：n，e，d，c，p，q [用于特殊方法的：hbop（high bits of factor），pbits（bits lenth of p）]
不用区分大小写，如: n或者N都行
多组密钥要区分顺序，不过只需区分同变量名的顺序，如出现的顺序: n1,n2,e1,e2 和 n1,e1,n2,e2 等价

按照上述操作后，报错问题如下

查看文件格式为unix

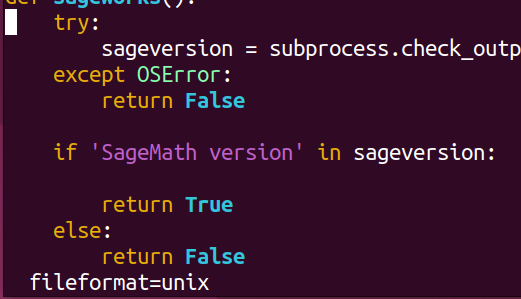
本文暂且使用目录下运行方法

python solve.py -i rsa.txt

How does it work

根据题目给的参数类型，自动判断应该采用哪种攻击方法，并尝试得到私钥或者明文，从而帮助CTFer快速拿到flag或解决其中的RSA考点。

例1：2020-BJDCTF-Crypto-rsa_output

n=21058339337354287847534107544613605305015441090508924094198816691219103399526800112802416383088995253908857460266726925615826895303377801614829364034624475195859997943146305588315939130777450485196290766249612340054354622516207681542973756257677388091926549655162490873849955783768663029138647079874278240867932127196686258800146911620730706734103611833179733264096475286491988063990431085380499075005629807702406676707841324660971173253100956362528346684752959937473852630145893796056675793646430793578265418255919376323796044588559726703858429311784705245069845938316802681575653653770883615525735690306674635167111
e=2767
c=20152490165522401747723193966902181151098731763998057421967155300933719378216342043730801302534978403741086887969040721959533190058342762057359432663717825826365444996915469039056428416166173920958243044831404924113442512617599426876141184212121677500371236937127571802891321706587610393639446868836987170301813018218408886968263882123084155607494076330256934285171370758586535415136162861138898728910585138378884530819857478609791126971308624318454905992919405355751492789110009313138417265126117273710813843923143381276204802515910527468883224274829962479636527422350190210717694762908096944600267033351813929448599

n=21058339337354287847534107544613605305015441090508924094198816691219103399526800112802416383088995253908857460266726925615826895303377801614829364034624475195859997943146305588315939130777450485196290766249612340054354622516207681542973756257677388091926549655162490873849955783768663029138647079874278240867932127196686258800146911620730706734103611833179733264096475286491988063990431085380499075005629807702406676707841324660971173253100956362528346684752959937473852630145893796056675793646430793578265418255919376323796044588559726703858429311784705245069845938316802681575653653770883615525735690306674635167111
e=3659
c=11298697323140988812057735324285908480504721454145796535014418738959035245600679947297874517818928181509081545027056523790022598233918011261011973196386395689371526774785582326121959186195586069851592467637819366624044133661016373360885158956955263645614345881350494012328275215821306955212788282617812686548883151066866149060363482958708364726982908798340182288702101023393839781427386537230459436512613047311585875068008210818996941460156589314135010438362447522428206884944952639826677247819066812706835773107059567082822312300721049827013660418610265189288840247186598145741724084351633508492707755206886202876227

例2：费马分解（p&q相近时）

#!/usr/local/bin/python
# coding:utf-8
import argparse
from Crypto.PublicKey import RSA
import subprocess
import lib.RSAutils
import libnum

split_char_dic = ['=', ':', 'is']

# Check if sage is installed and working
def sageworks():
    try:
        sageversion = subprocess.check_output(['sage', '-v'])
    except OSError:
        return False

    if 'SageMath version' in sageversion:

        return True
    else:
        return False

def input_file(path):
    multiple = False
    with open(path) as dfile:
        data = {}
        data_lines = dfile.readlines()
        for i in split_char_dic:
            if i in data_lines[0]:
                split_char = i
                break
        for k in data_lines:
            if not k.strip():
                continue
            key = k.split(split_char)[0].strip().lower()
            value = k.split(split_char)[1].strip()
            value = long(int(value, 16)) if '0x' in value else long(int(value))
            if key in data and value != data[key]:
                if isinstance(data[key], list):
                    data[key].append(value)
                else:
                    data[key] = [data[key], value]
                multiple = True
            else:
                data[key] = value
    return data, multiple

if __name__ == "__main__":
    parser = argparse.ArgumentParser(
        description='It helps CTFer to get first blood of RSA-base CTF problems')

    # group1用于指定是否需要打印私钥及待解密的密文或者自动识别的文本
    group1 = parser.add_mutually_exclusive_group(required=True)
    # 密文可以指定密文文件，也可以指定它对应的十进制值
    group1.add_argument(
        '--decrypt', help='decrypt a file, usually like "flag.enc"', default=None)
    group1.add_argument(
        '-c', '--decrypt_int', type=long, help='decrypt a long int num', default=None)
    group1.add_argument(
        '--private', help='Print private key if recovered', action='store_true')
    group1.add_argument(
        '-i', '--input', help='input a file with all necessary parameters (see examples/input_example.txt)')
    group1.add_argument(
        '-g', '--gadget', help='Use some gadgets to pre-process your data first', action='store_true')

    group2 = parser.add_argument_group(
        title='some gadgets', description='Pre-process your data (with --gadget together)')
    group2.add_argument(
        '--createpub', help='Take N and e and output to file specified by "-o" or just print it', action='store_true')
    group2.add_argument(
        '-o', "--output", help='Specify the output file path in --createpub mode.')
    group2.add_argument(
        '--dumpkey', help='Just print the RSA variables from a key - n,e,d,p,q', action='store_true')
    group2.add_argument(
        '--enc2dec', help='get cipher (in decimalism) from a encrypted file')

    # group3用于指定一个密钥pem文件 ，或指定需要的模数值
    group3 = parser.add_argument_group(
        title='the RSA variables', description='Specify the variables whatever you got')
    group3.add_argument(
        '-k', '--key', help='pem file, usually like ".pub" or ".pem", and it begins with "-----BEGIN"')
    group3.add_argument('-N', type=long, help='the modulus')
    group3.add_argument('-e', type=long, help='the public exponent')
    group3.add_argument('-d', type=long, help='the private exponent')
    group3.add_argument('-p', type=long, help='one factor of modulus')
    group3.add_argument('-q', type=long, help='one factor of modulus')

    # group4用于指定一特殊方法中所需要的额外参数
    group4 = parser.add_argument_group(
        title='extra variables', description='Used in some special methods')
    group4.add_argument('--KHBFA', type=long,
                        help='use Known High Bits Factor Attack, this specify the High Bits of factor', default=None)
    group4.add_argument('--pbits', type=long,
                        help='customize the bits lenth of factor, default is half of n`s bits lenth', default=None)

    parser.add_argument(
        '-v', '--verbose', help='print details', action='store_true')
    args = parser.parse_args()

    # if createpub mode generate public key then quit
    if args.createpub:
        if args.N is None or args.e is None:
            raise Exception(
                "Specify both a modulus and exponent on the command line. See --help for info.")
        if args.output:
            with open(args.output, 'w') as file:
                file.write(RSA.construct(
                    (args.N, args.e)).publickey().exportKey())
            print 'saved in %s' % args.output
        else:
            print RSA.construct((args.N, args.e)).publickey().exportKey()
        quit()

    # if dumpkey mode dump the key components then quit
    if args.dumpkey:
        if args.key is None:
            raise Exception(
                "Specify a key file to dump with --key. See --help for info.")

        key_data = open(args.key, 'rb').read()
        key = RSA.importKey(key_data)
        print "[*] n: " + str(key.n)
        print "[*] e: " + str(key.e)
        if key.has_private():
            print "[*] d: " + str(key.d)
            print "[*] p: " + str(key.p)
            print "[*] q: " + str(key.q)
        quit()

    # if enc2dec mode print cipher in dec then quit
    if args.enc2dec:
        enc_data = open(args.enc2dec, 'r').read()
        print "[*] c : " + str(libnum.s2n(enc_data))
        quit()

    if sageworks():
        args.sageworks = True
    else:
        args.sageworks = False
    if args.input:
        args.data, args.multiple = input_file(args.input)
    else:
        args.data, args.multiple = None, False
    attackobj = lib.RSAutils.RSAAttack(args)
    attackobj.attack()

已实现的攻击方法

• 大整数分解

• • 检查过去的ctf比赛中出现的素数- Gimmicky Primes method- Wiener's attack- factordb在线分解N- Small q (q < 100,000)- 费马分解（p&q相近时）- Boneh Durfee Method (d < n^0.292)- Small fractions method when p/q is close to a small fraction

• Basic Broadcast Attack

• Known High Bits Factor Attack

• Common factor between ciphertext and modulus attack

• 小公钥指数攻击

• Rabin 算法

• 模不互素

• 共模攻击

• d泄露攻击

注：没有RSA-CRT算法，参数类型中不识别dp，dq变量名

basecrack

一个用Python编写的工具，可以解码所有字母数字基本编码方案。该工具可以接受单个用户输入，来自文件的多个输入，来自参数的输入，多编码基础，图像EXIF数据中的基数，基于具有OCR的图像并解码它们的速度非常快。

注意：建议使用python3

完成安装后如下

python3 basecrack.py -h

![](https://img-blog.csdnimg.cn/3a134af6cdbb4edfbed8e9667bdde328.png)

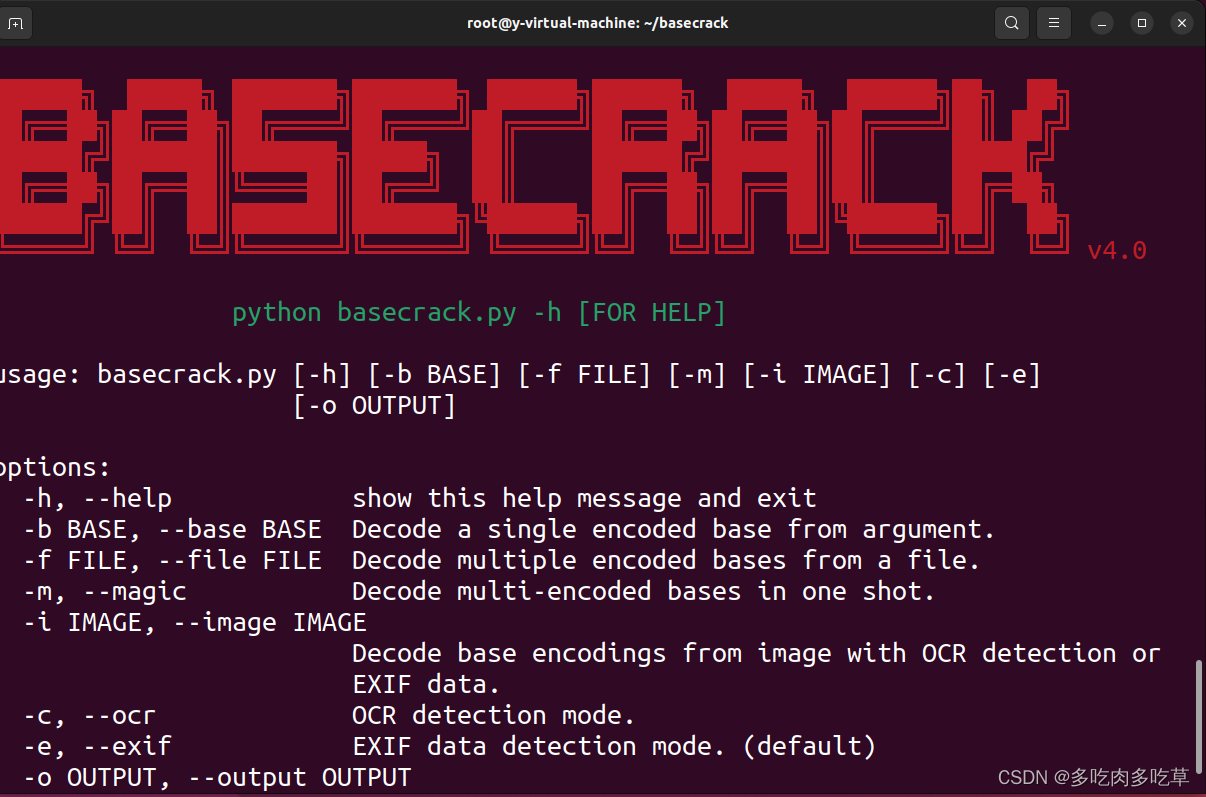
给basecrack文件夹解锁

chmod -r 'xxxxxx'

例1：base家族套娃

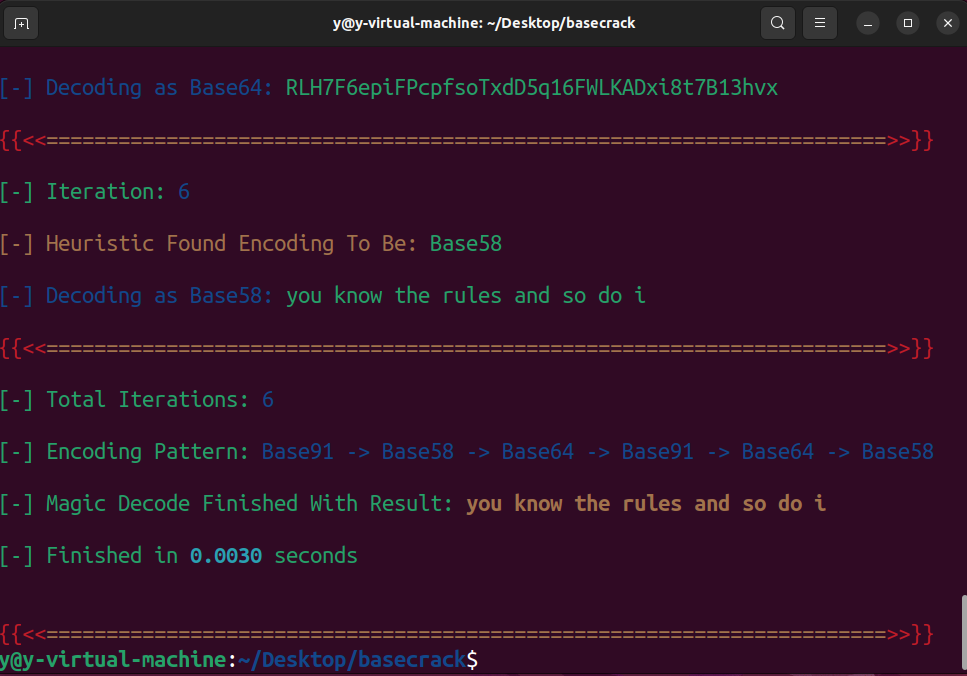
Crypto-attacks

Python implementations of cryptographic attacks and utilities.

注意：需要

• SageMath with Python 3.9
• PyCryptodome

Usage

You can also call the attacks from other Python files, but then you'll have to fix the Python path yourself.

例1: Github上的实例

sage -python attacks/rsa/boneh_durfee.py

运行报错，出现模块弃用等一些问题

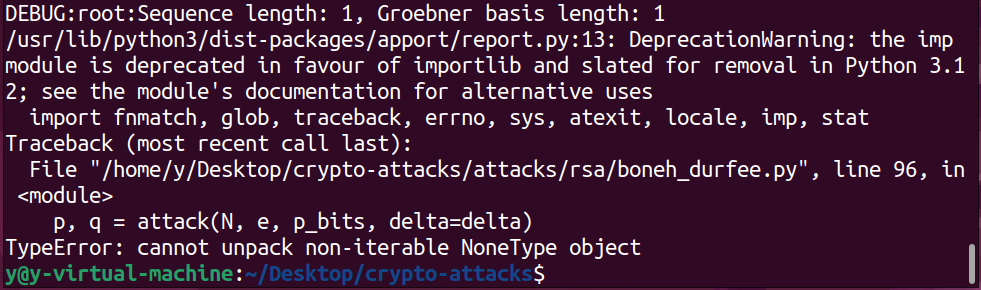
正常运行原文件没有问题，而按教程在py文件底部添加如下代码之后跑不通。

import logging

# Some logging so we can see what's happening.
logging.basicConfig(level=logging.DEBUG)

N = 88320836926176610260238895174120738360949322009576866758081671082752401596826820274141832913391890604999466444724537056453777218596634375604879123818123658076245218807184443147162102569631427096787406420042132112746340310992380094474893565028303466135529032341382899333117011402408049370805729286122880037249
e = 36224751658507610673165956970793195381480143363550601971796688201449789736497322700382657163240771111376677180786660893671085854060092736865293791299460933460067267613023891500397200389824179925263846148644777638774319680682025117466596019474987378275216579013846855328009375540444176771945272078755317168511
p_bits = 512
delta = 0.26

p, q = attack(N, e, p_bits, delta=delta)
assert p * q == N
print(f"Found p = {p} and q = {q}")

可以针对以实现的一些攻击方法的python脚本来进行学习。

Implemented attacks

Approximate Common Divisor
CBC
CBC + CBC-MAC
CBC-MAC
CTR
ECB
Elliptic Curve Cryptography
ElGamal Encryption
ElgGamal Signature
Factorization
Hidden Number Problem
GCM
IGE
Knapsack Cryptosystems
Linear Congruential Generators
Learning With Errors
Mersenne Twister
One-time Pad
Pseudoprimes
RC4
RSA
Shamir's Secret Sharing
Other interesting implementations
Elliptic Curve Generation
Small Roots

Openssl

openssl是一个功能丰富且自包含的开源安全工具箱。openssl还支持许多加密算法，例如RSA、DSA、ECDSA、ECDHE、Diffie–Hellman key exchange等。

openssl采用C语言作为开发语言，这使得它具有优秀的跨平台性能。

本文初步介绍Ubuntu下自带的OpenSSL在CTF解题当中的应用。

关于RSA中pem文件的加解密

pem文件

pem格式的文件通常用于数字证书认证机构(Certificate Authorities，CA)，其文件形式主要为base64编码的文件，头尾有类似于-----BEGIN PUBLIC KEY-----和-----END PUBLIC KEY-----的头尾标记。

解析公私钥

openssl rsa [-inform PEM|NET|DER] [-outform PEM|NET|DER] [-in filename] [-passin arg] [-out filename] [-passout arg]
       [-sgckey] [-des] [-des3] [-idea] [-text] [-noout] [-modulus] [-check] [-pubin] [-pubout] [-engine id]
常用选项：
-in filename：指明私钥文件
-out filename：指明将提取出的公钥保存至指定文件中 
-pubout：根据私钥提取出公钥 
基本命令：
openssl rsa -pubin -text -modulus -in 1.pem       #读取公钥
openssl rsa -in 1.pem -text                          #读取私钥