数组中的最大间距（巨难）

1.对应letecode链接：

1. 最大间距 - 力扣（LeetCode）

2.题目描述：

3.解题思路：

1.我们很容易就能够想到时间复杂度为O（N*logN)的算法，然后再遍历一遍数组求相邻两个数的最大差值即可。但这与题目要求的时间复杂度O（N）不符。

下面我们来看一下这种不是人能够想得到的解法：

2.利用计数排序的思想，先求出原数组的最大值

max

与最小值

min

.

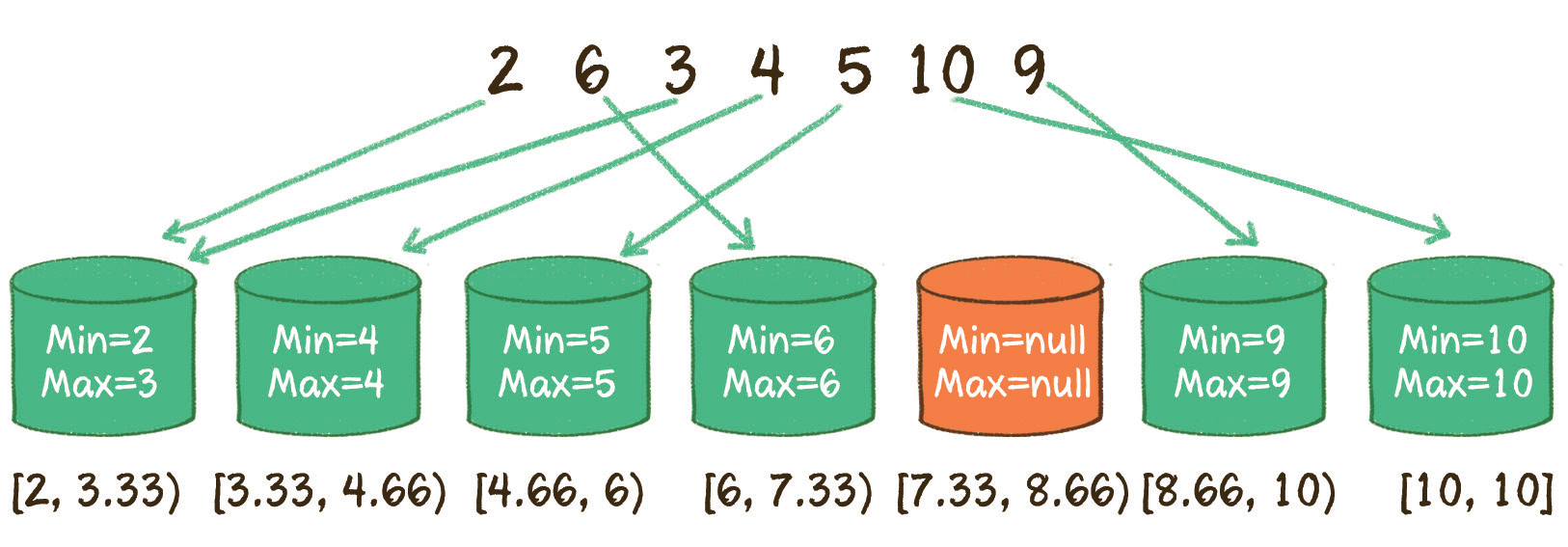
利用桶排序的思想，根据原数组的长度 n，创建出 n 个桶，每一个桶代表一个区间范围。其中第 0个桶从原数组的最小值 min 开始，区间跨度为(max - min) / (n - 1)。下面我们以无序数组

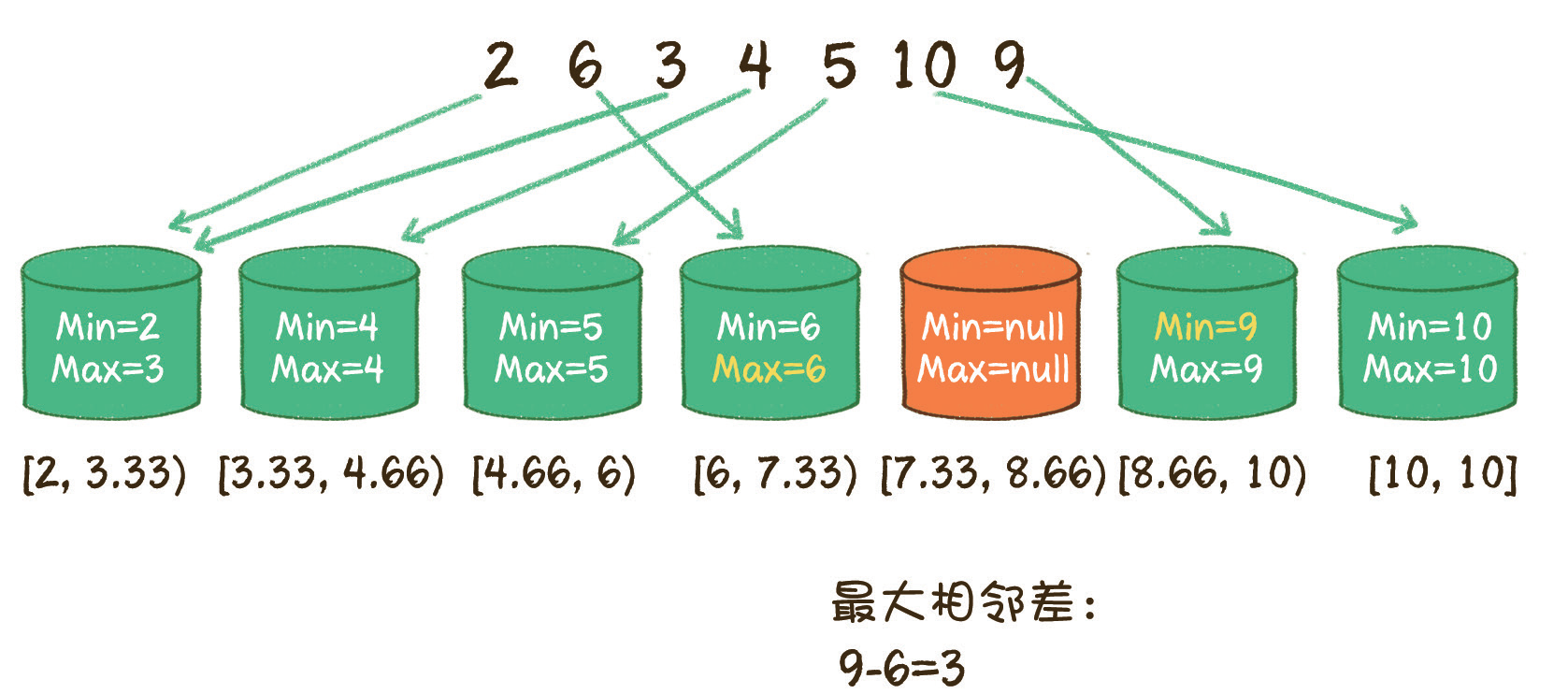
{ 2, 6, 3, 4, 5, 10, 9 }为例：

3.遍历所有的桶，统计出每一个桶的最大值，和这个桶右侧非空桶的最小值的差，数值最大的差即为原数组排序后的相邻最大差值

第 2 步，遍历原数组，确定每个桶内的最大和最小值。

3.遍历原数组，把原数组每一个元素插入到对应的桶中，记录每一个桶的最大和最小值。

4.对应代码：

class Solution {
public:
    int maximumGap(vector<int>& nums) {
          if(nums.size()<2){
              return 0;
          }
          int len=nums.size();
          int MaxVal=INT_MIN;
          int MinVal=INT_MAX;
          for(auto ch:nums)
          {
              MaxVal=max(MaxVal,ch);
              MinVal=min(MinVal,ch);
          }
          if(MinVal==MaxVal){//说明只有一种数
              return 0;
          }
          //不止一种数一定有range,len个数len+1一个桶
          vector<bool>hasNum(len+1);
          //保存第i号桶的最大值和最小值
          vector<int>maxs(len+1);
          vector<int>mins(len+1);
          int bid=0;
          for(int i=0;i<nums.size();i++){
            bid=bucket(nums[i],len,MinVal,MaxVal);//获取每个数应该去那个桶
            mins[bid]=hasNum[bid]?min(mins[bid],nums[i]):nums[i];//更新桶里面的最小值和最大值
            maxs[bid]=hasNum[bid]?max(maxs[bid],nums[i]):nums[i];
            hasNum[bid]=true;
          }
          int res=0;
          int lastMax=maxs[0];
          //答案不可能来自同一个桶内
          int i=1;
          for(;i<=len;i++){
              if(hasNum[i]){//计算差值
                  res=max(res,mins[i]-lastMax);
                  lastMax=maxs[i];
              }
          }
          return res;
    }

    int bucket(long num,long len,long Min,long Max){//确定桶号
        return (int)((num-Min)*len/(Max-Min));
    }

};

注意：代码实现这里N个数对应N+1个桶原理类似。