基于卷积神经网络（cnn）的手写数字识别（PyTorch）

1.1 卷积神经网络简介

卷积神经网络（Convolutional Neural Networks，简称：CNN）是深度学习当中一个非常重要的神经网络结构。它主要用于用在图像图片处理，视频处理，音频处理以及自然语言处理等等。
早在上世纪80年代左右，卷积神经网络的概念就已经被提出来了。但其真正的崛起却是在21世纪之后，21世纪之后，随着深度学习理论的不断完善，同时，由计算机硬件性能的提升，计算机算力的不断发展，给卷积神经网络这种算法提供了应用的空间。著名的AlphaGo，手机上的人脸识别，大多数都是采用卷积神经网络。因此可以说，卷积神经网络在如今的深度学习领域，有着举足轻重的作用。

在了解卷积神经网络之前，我们务必要知道：什么是神经网络（Neural Networks），关于这个，我们已经在深度学习简介的 第二部分有所介绍。这里就不赘述了。在了解了神经网络的基础上，我们再来探究：卷积神经网络又是什么呢？当中的“卷积”这个词，又意味着什么呢？

1.2 神经网络

1.2.1 神经元模型

人工神神经网络(neural networks)方面的研究很早就已出现，今天“神经网络” 已是一个相当大的、多学科交叉的学科领域.各相关学科对神经网络的定义多种多样。简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应” 。
神经网络中最基本的成分是神经元(neuron)模型,即上述定义中的“简单单元”，在生物神经网络中,每个神经元与其他神经元相连,当它“兴奋”时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过了一个“阈值”(threshold),那么它就会被激活,即“兴奋”起来,向其他神经元发送化学物质。在这个模型中，神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接(connection)进行传递,神经元接收到的总输入值将与神经元的间值进行比较，然后通过激活函数处理，产生神经元输出。

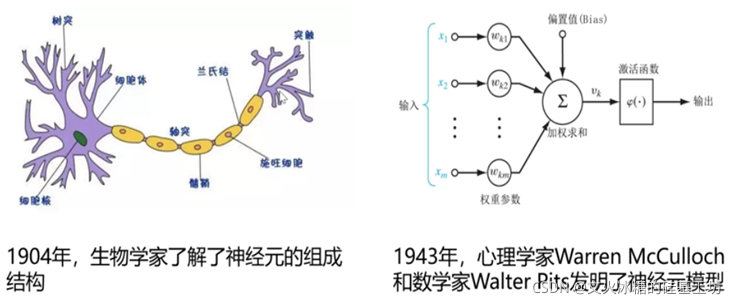
1.2.2 神经网络模型

 神经网络是一种运算模型，由大量的节点（或称神经元）之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数（activation function）。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。

1.3 卷积神经网络

1.3.1卷积的概念

卷积神经网络与普通神经网络的区别在于，卷积神经网络包含了一个由卷积层和子采样层（池化层）构成的特征抽取器。在卷积神经网络的卷积层中，一个神经元只与部分邻层神经元连接。在CNN的一个卷积层中，通常包含若干个特征图(featureMap)，每个特征图由一些矩形排列的的神经元组成，同一特征图的神经元共享权值，这里共享的权值就是卷积核。卷积核一般以随机小数矩阵的形式初始化，在网络的训练过程中卷积核将学习得到合理的权值。共享权值（卷积核）带来的直接好处是减少网络各层之间的连接，同时又降低了过拟合的风险。子采样也叫做池化（pooling），通常有均值子采样（mean pooling）和最大值子采样（max pooling）两种形式。子采样可以看作一种特殊的卷积过程。卷积和子采样大大简化了模型复杂度，减少了模型的参数。

1.3.2 卷积的计算过程

假设我们输入的是551的图像，中间的那个331是我们定义的一个卷积核（简单来说可以看做一个矩阵形式运算器），通过原始输入图像和卷积核做运算可以得到绿色部分的结果，怎么样的运算呢？实际很简单就是我们看左图中深色部分，处于中间的数字是图像的像素，处于右下角的数字是我们卷积核的数字，只要对应相乘再相加就可以得到结果。例如图中‘30+11+22+22+02+00+20+01+0*2=9’

计算过程如下动图：

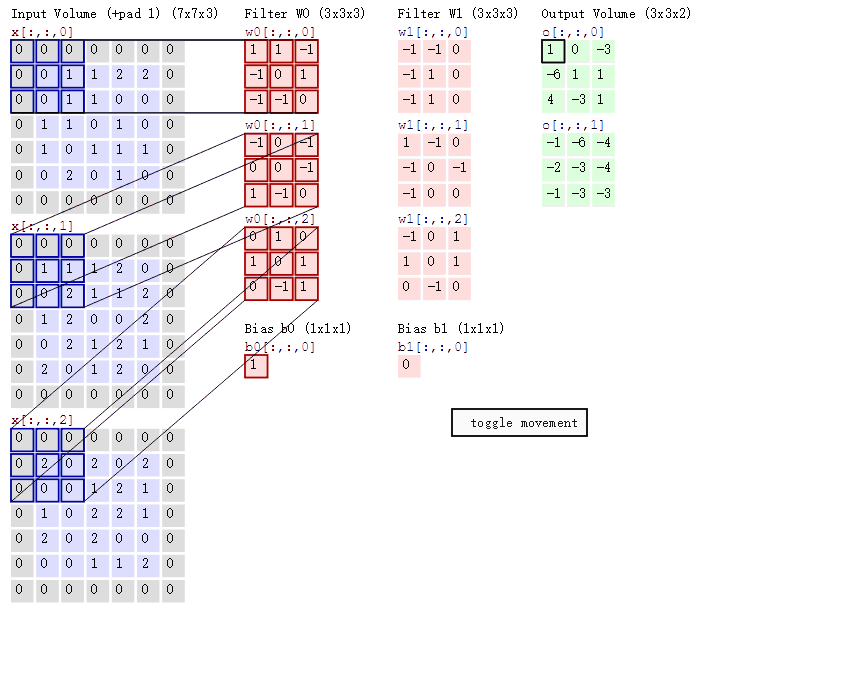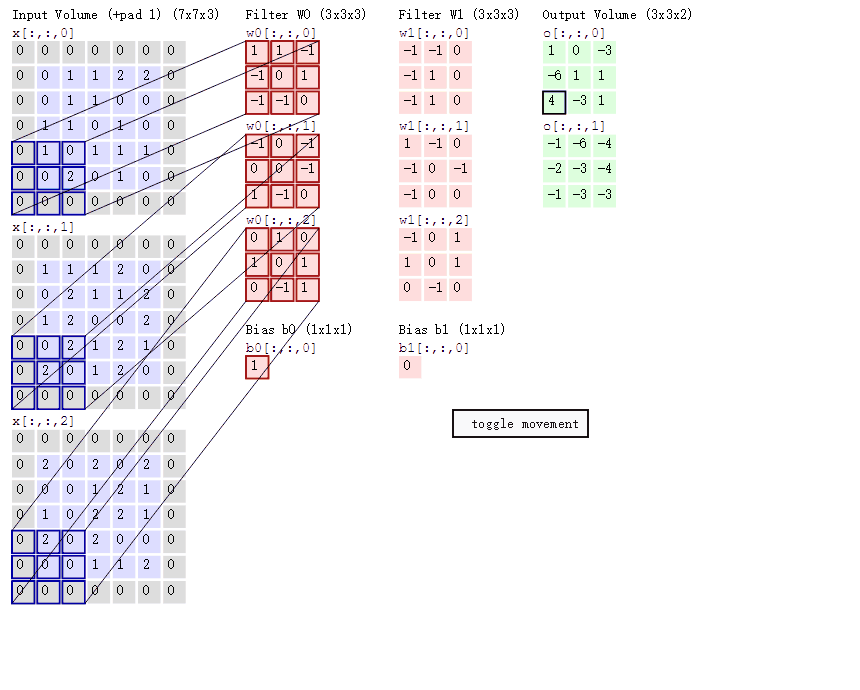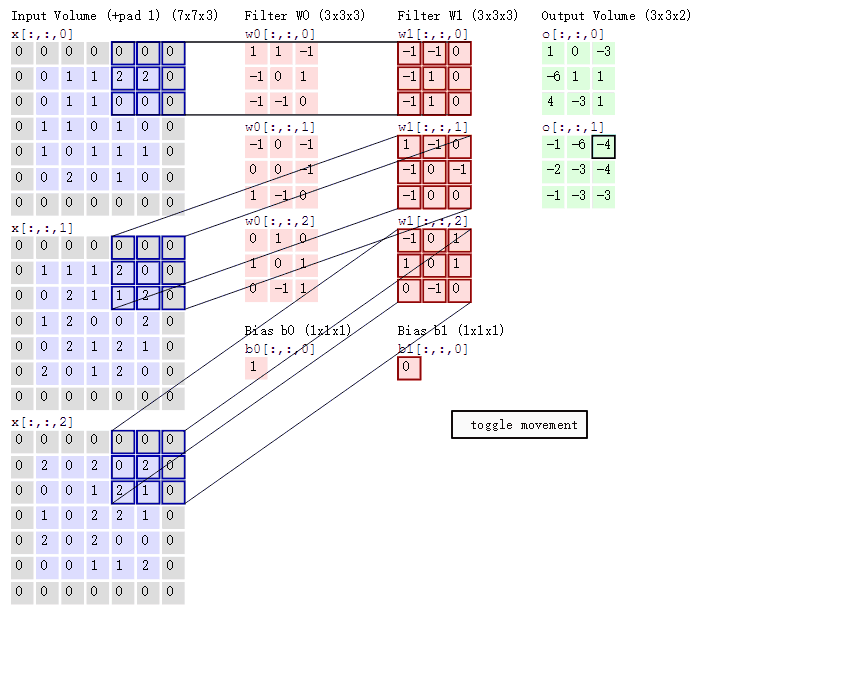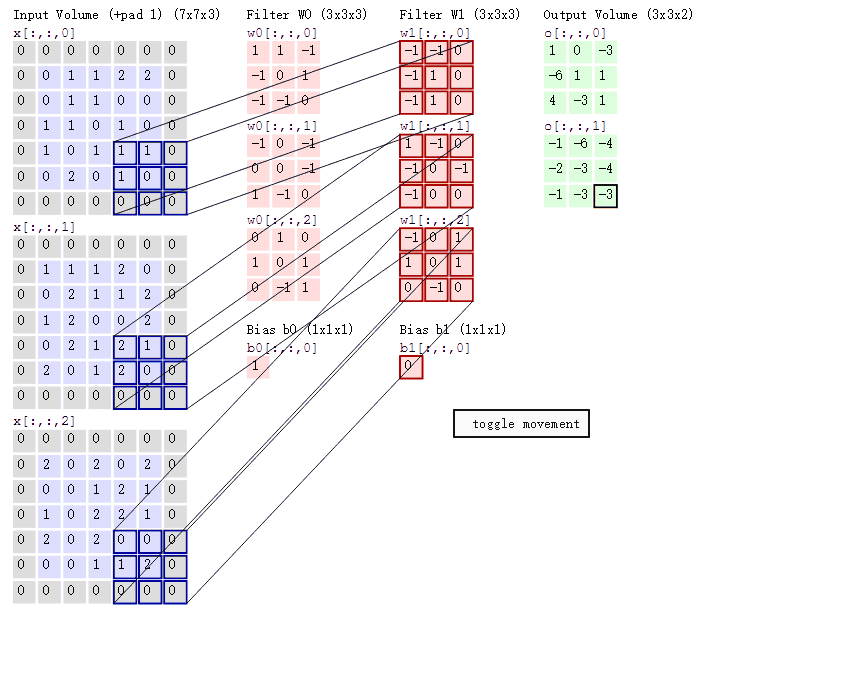
图中最左边的三个输入矩阵就是我们的相当于输入d=3时有三个通道图，每个通道图都有一个属于自己通道的卷积核，我们可以看到输出（output）的只有两个特征图意味着我们设置的输出d=2，有几个输出通道就有几层卷积核（比如图中就有FilterW0和FilterW1），这意味着我们的卷积核数量就是输入d的个数乘以输出d的个数（图中就是2*3=6个），其中每一层通道图的计算与上文中提到的一层计算相同，再把每一个通道输出的输出再加起来就是绿色的输出数字。

1.3.3 感受野

感受野（Receptive Field）：卷积神经网络各输出层每个像素点在原始图像上的映射区域大小。
下图为感受野示意图：

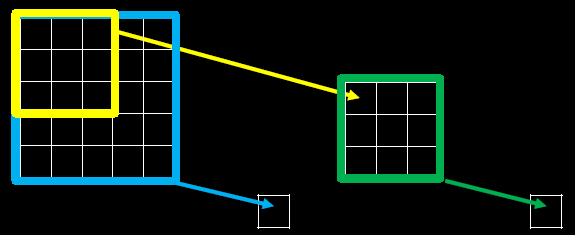
当我们采用尺寸不同的卷积核时，最大的区别就是感受野的大小不同，所以经常会采用多层小卷积核来替换一层大卷积核，在保持感受野相同的情况下减少参数量和计算量。
例如十分常见的用2层3 * 3卷积核来替换1层5 * 5卷积核的方法，如下图所示。

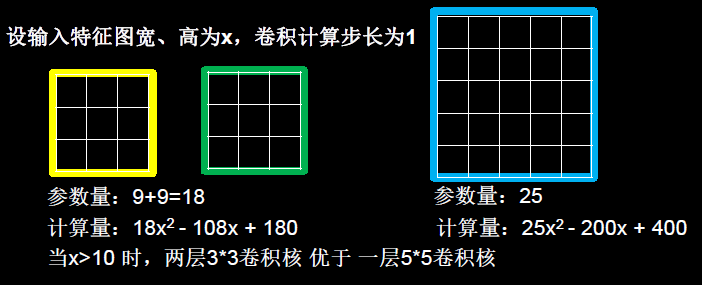
1.3.4 步长

每次卷积核移动的大小。

1.3.5 输出特征尺寸计算

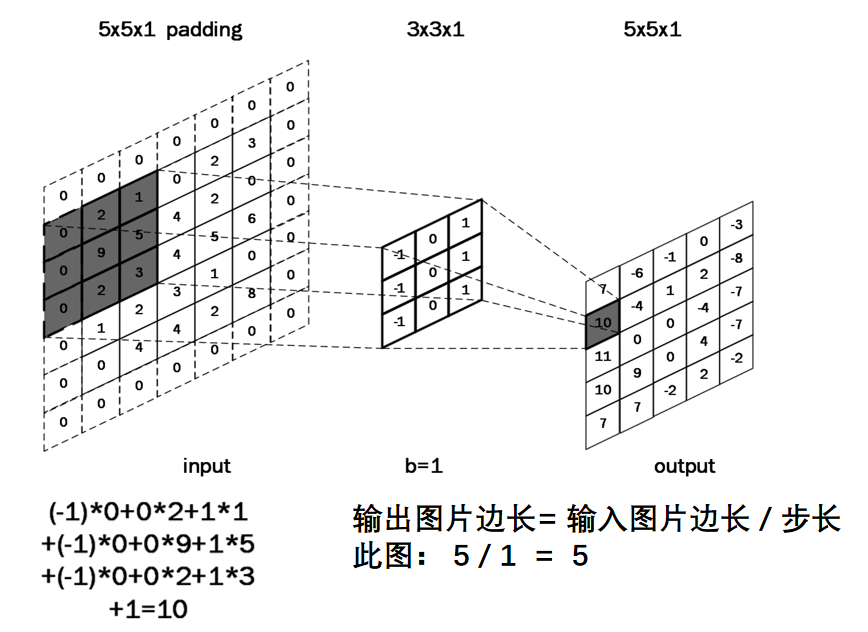
输出特征尺寸计算：在了解神经网络中卷积计算的整个过程后，就可以对输出特征图的尺寸进行计算。如下图所示，5×5的图像经过3×3大小的卷积核做卷积计算后输出特征尺寸为3×3

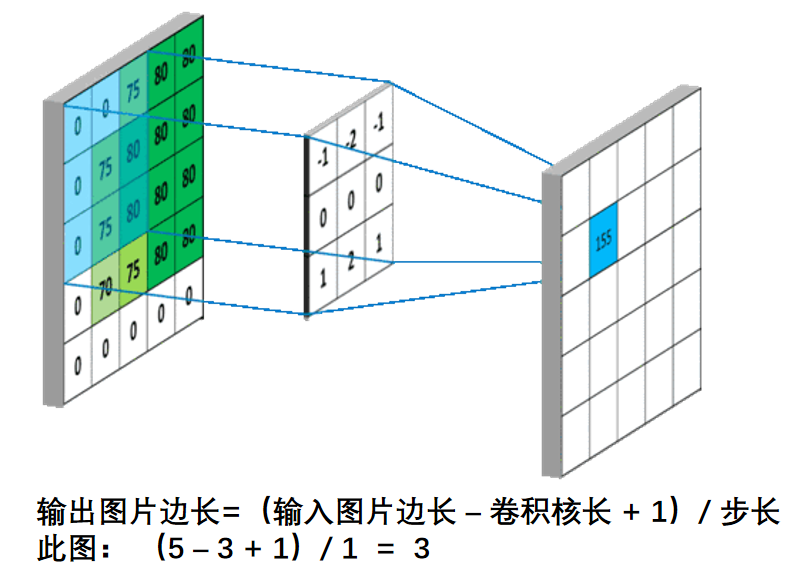
1.3.6 全零填充

当卷积核尺寸大于 1 时，输出特征图的尺寸会小于输入图片尺寸。如果经过多次卷积，输出图片尺寸会不断减小。为了避免卷积之后图片尺寸变小，通常会在图片的外围进行填充(padding)，如下图所示

全零填充（padding）：为了保持输出图像尺寸与输入图像一致，经常会在输入图像周围进行全零填充，如下所示，在5×5的输入图像周围填0，则输出特征尺寸同为5×5。

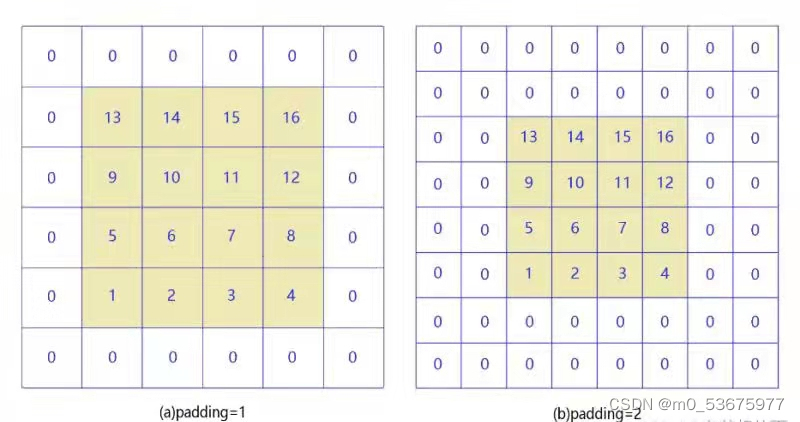
当padding=1和paadding=2时，如下图所示：

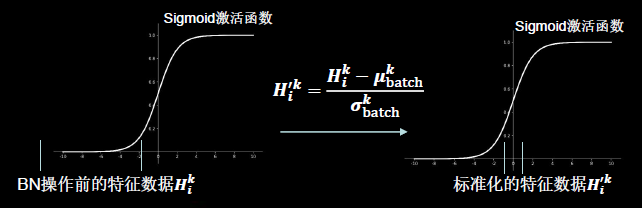
1.3.7 标准化

使数据符合0均值，1为标准差的分布。
批标准化（Batch Normalization）：对一小批数据（batch），做标准化处理。

Batch Normalization将神经网络每层的输入都调整到均值为0，方差为1的标准正态分布，其目的是解决神经网络中梯度消失的问题.

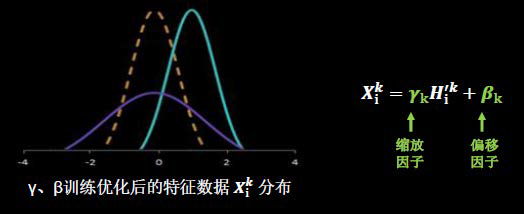
BN操作的另一个重要步骤是缩放和偏移，值得注意的是，缩放因子γ以及偏移因子β都是可训练参数。

1.3.7 池化层

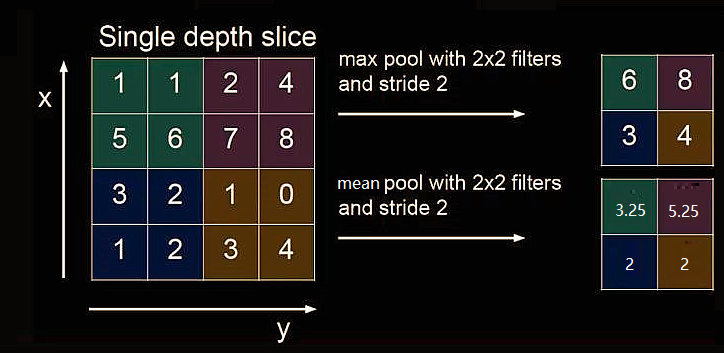
池化（Pooling）用于减少特征数据量。
最大值池化可提取图片纹理，均值池化可保留背景特征

1.4 卷积神经网络的全过程

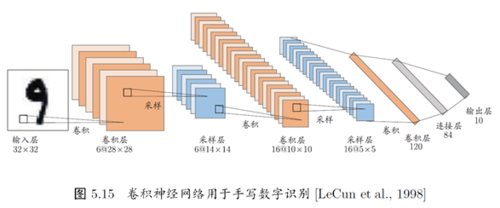
1.5 PyTorch的卷积神经网络（cnn）手写数字识别

使用的框架为pytorch。

数据集：MNIST数据集，60000张训练图像，每张图像size为28*28。

可在http://yann.lecun.com/exdb/mnist/中获取

1.5.1 代码

import torch
import torch.nn as nn
import torchvision.datasets as dataset
import torchvision.transforms as transforms
import torch.utils.data as data_utils

#获取数据集
train_data=dataset.MNIST(root="D",
                         train=True,
                         transform=transforms.ToTensor(),
                         download=True
                         )
test_data=dataset.MNIST(root="D",
                         train=False,
                         transform=transforms.ToTensor(),
                         download=False
                         )
train_loader=data_utils.DataLoader(dataset=train_data, batch_size=100, shuffle=True)
test_loader=data_utils.DataLoader(dataset=test_data, batch_size=100, shuffle=True)

#创建网络
class Net(torch.nn.Module):
   def __init__(self):
        super().__init__()
        self.conv=nn.Conv2d(1, 32, kernel_size=5, padding=2)
        self.bat2d=nn.BatchNorm2d(32)
        self.relu=nn.ReLU()
        self.pool=nn.MaxPool2d(2)
        self.linear=nn.Linear(14 * 14 * 32, 70)
        self.tanh=nn.Tanh()
        self.linear1=nn.Linear(70,30)
        self.linear2=nn.Linear(30, 10)
   def forward(self,x):
        y=self.conv(x)
        y=self.bat2d(y)
        y=self.relu(y)
        y=self.pool(y)
        y=y.view(y.size()[0],-1)
        y=self.linear(y)
        y=self.tanh(y)
        y=self.linear1(y)
        y=self.tanh(y)
        y=self.linear2(y)
        return y
cnn=Net()
cnn=cnn.cuda()

#损失函数
los=torch.nn.CrossEntropyLoss()

#优化函数
optime=torch.optim.Adam(cnn.parameters(), lr=0.01)

#训练模型
for epo in range(10):
   for i, (images,lab) in enumerate(train_loader):
        images=images.cuda()
        lab=lab.cuda()
        out = cnn(images)
        loss=los(out,lab)
        optime.zero_grad()
        loss.backward()
        optime.step()
        print("epo:{},i:{},loss:{}".format(epo+1,i,loss))

#测试模型
loss_test=0
accuracy=0
with torch.no_grad():
   for j, (images_test,lab_test) in enumerate(test_loader):
        images_test = images_test.cuda()
        lab_test=lab_test.cuda()
        out1 = cnn(images_test)
        loss_test+=los(out1,lab_test)
        loss_test=loss_test/(len(test_data)//100)
        _,p=out1.max(1)
        accuracy += (p==lab_test).sum().item()
        accuracy=accuracy/len(test_data)
        print("loss_test:{},accuracy:{}".format(loss_test,accuracy))