
爱德华·蒙克(Edvard Munch)的"蒙特卡洛赌场的轮盘桌"(1892)
蒙特卡洛方法的起源与发展
1945年,在第二次世界大战即将结束之际,一场看似简单的纸牌游戏引发了计算领域的重大突破。这项突破最终导致了蒙特卡洛方法的诞生。参与曼哈顿计划的科学家斯坦尼斯劳·乌拉姆在康复期间深入思考了纸牌游戏中的概率问题。他意识到通过反复模拟,可以有效地近似复杂的概率问题。随后乌拉姆与同事约翰·冯·诺依曼讨论了这一想法,共同奠定了蒙特卡洛方法的理论基础。该方法的命名灵感来自摩纳哥著名的蒙特卡洛赌场,象征着其处理高风险和不确定性的特性。
时至今日,蒙特卡洛方法已成为机器学习领域的关键工具,在强化学习、贝叶斯滤波和复杂模型优化等方面有广泛应用。其强大的适应性和多样性使其在诞生七十多年后仍然保持着重要地位。从乌拉姆的纸牌游戏到现代复杂的人工智能应用,蒙特卡洛方法持续证明了其在处理复杂系统中的价值。
蒙特卡洛模拟的基本原理
在数据科学和机器学习领域,蒙特卡洛模拟提供了一种处理不确定性的有效方法。这种统计技术允许我们在面对复杂问题时,通过概率性方法进行决策。本文将深入探讨蒙特卡洛模拟的原理,并展示其在统计和机器学习中的实际应用。
我们首先会详细介绍蒙特卡洛模拟的理论基础,阐明其作为强大问题解决工具的核心原理。然后将通过Python实现来展示蒙特卡洛模拟的实际应用。
最后我们将重点讨论如何利用蒙特卡洛模拟来优化机器学习模型。特别是在超参数调优这一常见挑战中,蒙特卡洛方法如何提供有效的解决方案。
理解蒙特卡洛模拟
蒙特卡洛模拟是数学家和数据科学家常用的一种重要技术。它提供了一种在复杂可能性空间中进行探索的方法,通过形成基于概率的假设并逐步优化选择来寻找最佳解决方案。
这种方法的核心是生成大量随机场景,遵循预定义的过程,然后分析这些场景以估计各种结果的概率。一个形象的类比是将每个场景视为"狼人杀"游戏中的一轮。在这个游戏中,玩家通过收集证据来推断细节。每一轮都会排除某些可能性,使玩家逐步接近真相。同样,蒙特卡洛模拟中的每次迭代都提供了使我们更接近复杂问题解决方案的信息。
在机器学习领域,这些"场景"可以代表不同的模型配置、各种超参数集、数据集分割方法等。通过评估这些场景的结果,我们可以深入了解机器学习算法的行为,从而做出更明智的优化决策。
实例:估算圆周率π
为了直观理解蒙特卡洛模拟,我们可以考虑一个估算π值的例子。想象一个特殊的飞镖游戏:你被蒙上眼睛,随机向一个大正方形飞镖靶投掷飞镖。这个正方形内有一个圆形目标。目标是通过这个游戏来估计π的值。
圆的面积与正方形面积的比率是π/4。因此,如果投掷大量飞镖,落在圆内的飞镖数量与总飞镖数量的比率应该近似于π/4。将这个比率乘以4,就得到了π的估计值。
随机猜测 vs. 蒙特卡洛方法
为了展示蒙特卡洛模拟的优势,我们将其与简单的随机猜测方法进行比较。以下代码实现了这两种方法:
#Random Guessing of Pi
# 导入必要的库
importrandom
importplotly.graph_objectsasgo
importnumpyasnp
# 设置猜测次数
num_guesses=6
# 生成单位圆的坐标
theta=np.linspace(0, 2*np.pi, 100)
unit_circle_x=np.cos(theta)
unit_circle_y=np.sin(theta)
# 进行多次猜测
foriinrange(num_guesses):
# 在2到4之间随机猜测pi的值
pi_guess=random.uniform(2, 4)
# 根据猜测生成圆的坐标
radius=pi_guess/4
circle_x=radius*np.cos(theta)
circle_y=radius*np.sin(theta)
# 创建散点图
fig=go.Figure()
# 添加猜测的圆
fig.add_trace(go.Scatter(
x=circle_x,
y=circle_y,
mode='lines',
line=dict(
color='blue',
width=3
),
name='Estimated Circle'
))
# 添加单位圆
fig.add_trace(go.Scatter(
x=unit_circle_x,
y=unit_circle_y,
mode='lines',
line=dict(
color='green',
width=3
),
name='Unit Circle'
))
# 更新图形布局
fig.update_layout(
title=f"Fig1{chr(97+i)}: Randomly Guessing Pi: {pi_guess}",
width=600,
height=600,
xaxis=dict(
constrain="domain",
range=[-1, 1]
),
yaxis=dict(
scaleanchor="x",
scaleratio=1,
range=[-1, 1]
)
)
# 显示图形
fig.show()
这段代码生成了一系列图形(图1a到图1f),展示了随机猜测π值的结果。每次猜测都会生成一个不同大小的圆,与实际的单位圆(绿色)进行比较。
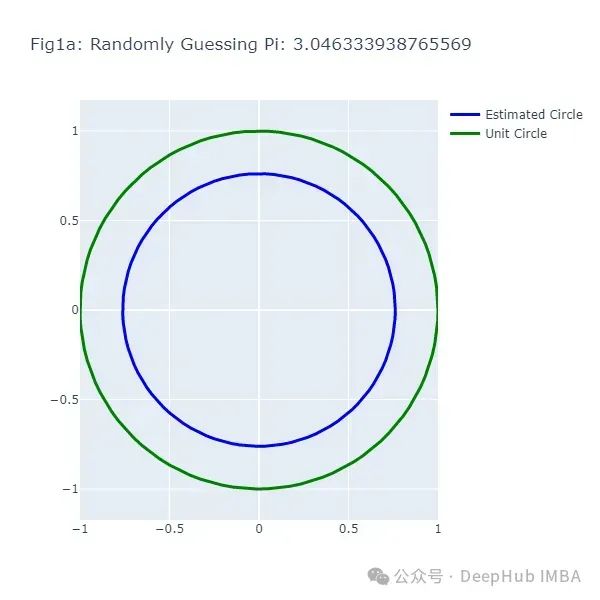
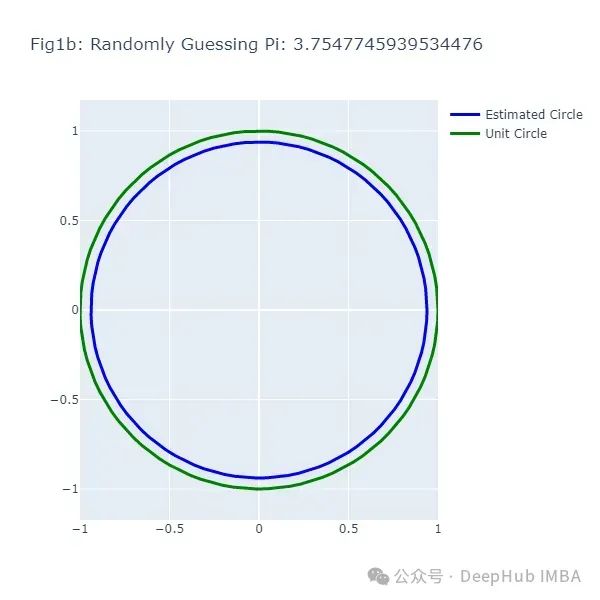
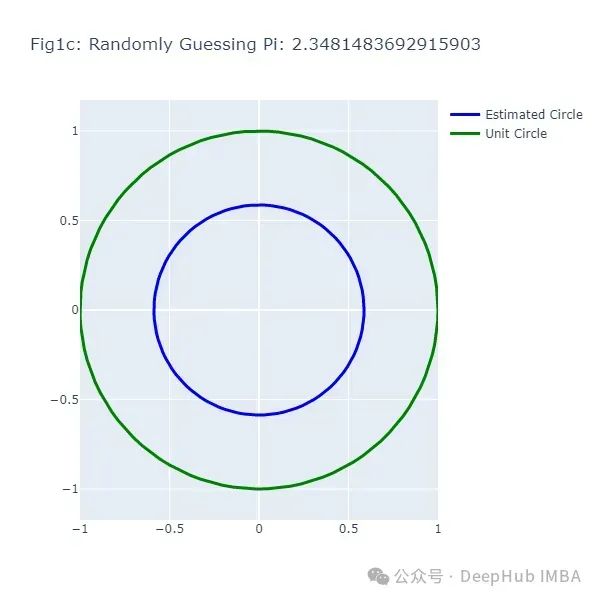
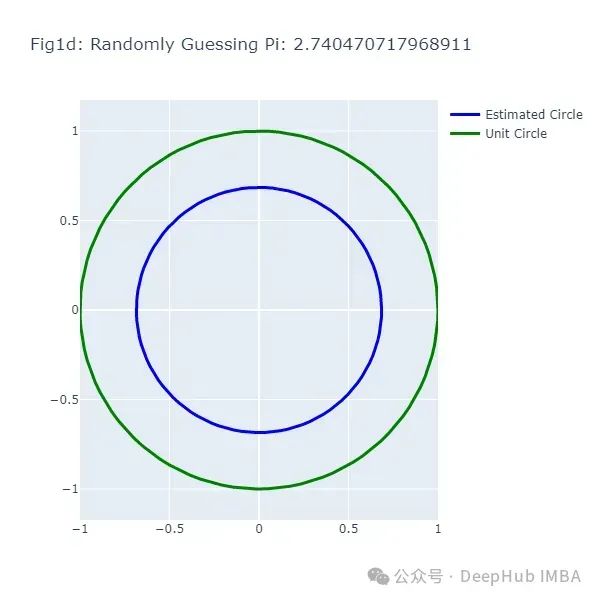
接下来,我们使用蒙特卡洛方法来估计π:
#Monte Carlo Estimation of Pi
# 导入必要的库
importrandom
importmath
importplotly.graph_objectsasgo
importplotly.ioaspio
importnumpyasnp
# 设置飞镖数量
num_darts=10000
darts_in_circle=0
# 存储飞镖坐标
x_coords_in, y_coords_in, x_coords_out, y_coords_out= [], [], [], []
# 设置图形数量
num_figures=6
darts_per_figure=num_darts//num_figures
# 生成单位圆
theta=np.linspace(0, 2*np.pi, 100)
unit_circle_x=np.cos(theta)
unit_circle_y=np.sin(theta)
# 模拟投掷飞镖
foriinrange(num_darts):
x, y=random.uniform(-1, 1), random.uniform(-1, 1)
ifmath.sqrt(x**2+y**2) <=1:
darts_in_circle+=1
x_coords_in.append(x)
y_coords_in.append(y)
else:
x_coords_out.append(x)
y_coords_out.append(y)
if (i+1) %darts_per_figure==0:
pi_estimate=4*darts_in_circle/ (i+1)
estimated_circle_radius=pi_estimate/4
estimated_circle_x=estimated_circle_radius*np.cos(theta)
estimated_circle_y=estimated_circle_radius*np.sin(theta)
fig=go.Figure()
fig.add_trace(go.Scattergl(x=x_coords_in, y=y_coords_in, mode='markers', name='Darts Inside Circle', marker=dict(color='green', size=4, opacity=0.8)))
fig.add_trace(go.Scattergl(x=x_coords_out, y=y_coords_out, mode='markers', name='Darts Outside Circle', marker=dict(color='red', size=4, opacity=0.8)))
fig.add_trace(go.Scatter(x=unit_circle_x, y=unit_circle_y, mode='lines', name='Unit Circle', line=dict(color='green', width=3)))
fig.add_trace(go.Scatter(x=estimated_circle_x, y=estimated_circle_y, mode='lines', name='Estimated Circle', line=dict(color='blue', width=3)))
fig.update_layout(title=f"Figure {chr(97+ (i+1) //darts_per_figure-1)}: Thrown Darts: {(i+1)}, Estimated Pi: {pi_estimate}", width=600, height=600, xaxis=dict(constrain="domain", range=[-1, 1]), yaxis=dict(scaleanchor="x", scaleratio=1, range=[-1, 1]), legend=dict(yanchor="top", y=0.99, xanchor="left", x=0.01))
fig.show()
pio.write_image(fig, f"fig2{chr(97+ (i+1) //darts_per_figure-1)}.png")
这段代码生成了另一系列图形(图2a到图2f),展示了使用蒙特卡洛方法估计π的过程。绿点表示落在圆内的飞镖,红点表示落在圆外的飞镖。
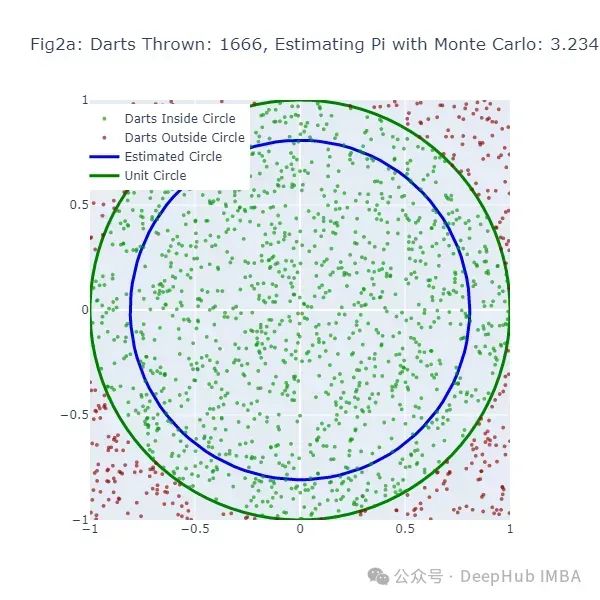



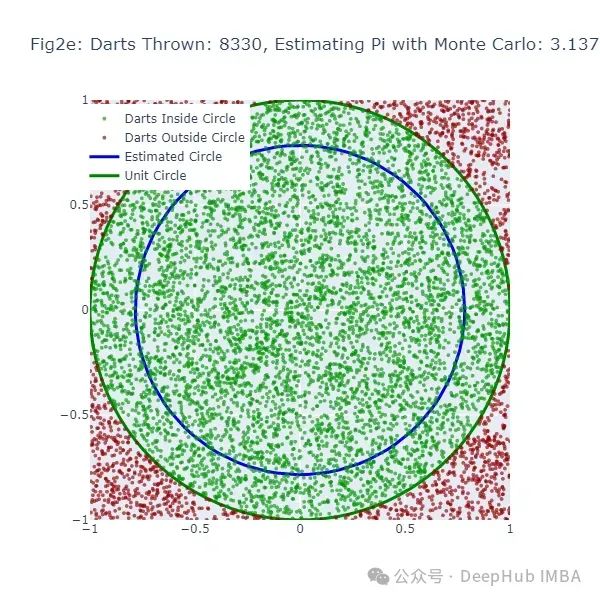

为了进一步验证蒙特卡洛方法的有效性,我们可以绘制一个图表,展示随着投掷飞镖数量的增加,估计值与真实π值之间的差异如何变化:
# 计算估计值与真实π的差异
diff_pi= [abs(estimate-math.pi) forestimateinpi_estimates]
# 创建图表
fig2g=go.Figure(data=go.Scatter(x=num_darts_thrown, y=diff_pi, mode='lines'))
# 添加标题和标签
fig2g.update_layout(
title="Fig2g: Darts Thrown vs Difference in Estimated Pi",
xaxis_title="Number of Darts Thrown",
yaxis_title="Difference in Pi",
)
# 显示图表
fig2g.show()
# 保存图表
pio.write_image(fig2g, "fig2g.png")
这个图表(图2g)展示了随着投掷飞镖数量的增加,估计值与真实π值之间的差异逐渐减小的趋势。
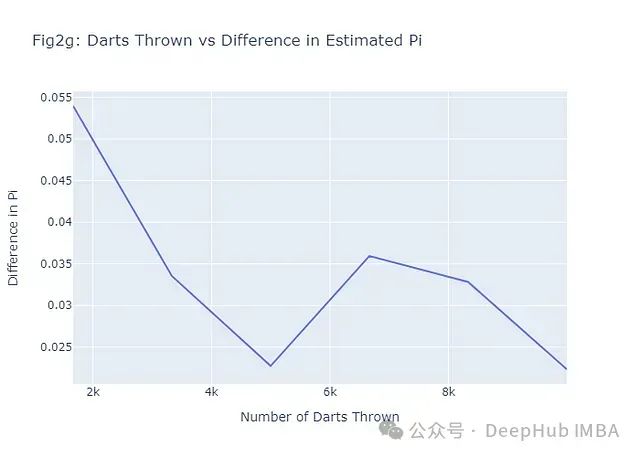
为了更全面地评估蒙特卡洛方法的性能,我们可以进行一个大规模的模拟:
# 500个蒙特卡洛场景,共投掷1,000,000个飞镖
importrandom
importmath
importplotly.graph_objectsasgo
importnumpyasnp
num_darts=1000000
darts_in_circle=0
num_scenarios=500
darts_per_scenario=num_darts//num_scenarios
darts_thrown_list= []
pi_diff_list= []
foriinrange(num_darts):
x, y=random.uniform(-1, 1), random.uniform(-1, 1)
ifmath.sqrt(x**2+y**2) <=1:
darts_in_circle+=1
if (i+1) %darts_per_scenario==0:
pi_estimate=4*darts_in_circle/ (i+1)
darts_thrown_list.append((i+1) /1000)
pi_diff_list.append(abs(pi_estimate-math.pi))
fig=go.Figure(data=go.Scattergl(x=darts_thrown_list, y=pi_diff_list, mode='markers'))
fig.update_layout(
title="Fig2h: Difference between Estimated and Actual Pi vs. Number of Darts Thrown (in thousands)",
xaxis_title="Number of Darts Thrown (in thousands)",
yaxis_title="Difference between Estimated and Actual Pi",
)
fig.show()
pio.write_image(fig, "fig2h.png")
这个大规模模拟(图2h)清晰地展示了随着样本量增加,蒙特卡洛方法估计的精确度如何提高。
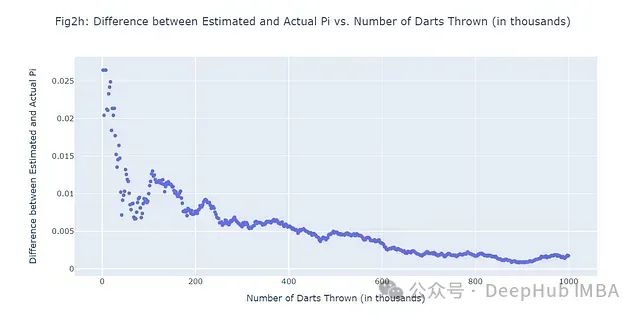
蒙特卡洛模拟在机器学习中的应用
蒙特卡洛模拟在机器学习领域有广泛的应用,其中一个重要应用是超参数调优。超参数是在机器学习算法训练之前需要设置的参数,它们不是通过训练过程学习得到的。例如在决策树中,树的最大深度是一个超参数;在神经网络中,学习率和隐藏层的数量都是超参数。
选择适当的超参数对模型性能有显著影响。一般来说研究者使用网格搜索或随机搜索来调整超参数。但是当超参数数量增加或取值范围扩大时,这些方法可能变得计算密集且耗时。蒙特卡洛模拟提供了一种更高效的替代方案,通过随机采样超参数空间,可以更快地找到优质的超参数组合。
下面我们将使用一个实际数据集来演示如何应用蒙特卡洛模拟进行超参数调优。
心脏病数据集分析
我们将使用UCI机器学习存储库中的心脏病数据集。这个数据集包含了患者的各种医疗指标,其中一些患有心脏病。数据集包含14个属性,如年龄、性别、胸痛类型、血压等。我们的目标是预测患者是否患有心脏病,这是一个二元分类问题。
首先,让我们加载并查看数据:
importpandasaspd
fromsklearn.model_selectionimporttrain_test_split
fromsklearn.preprocessingimportStandardScaler, OneHotEncoder
fromsklearn.composeimportColumnTransformer
fromsklearn.pipelineimportPipeline
fromsklearn.linear_modelimportLogisticRegression
fromsklearn.model_selectionimportGridSearchCV
fromsklearn.metricsimportroc_auc_score
importnumpyasnp
importplotly.graph_objectsasgo
url="https://archive.ics.uci.edu/ml/machine-learning-databases/heart-disease/processed.cleveland.data"
column_names= ["age", "sex", "cp", "trestbps", "chol", "fbs", "restecg", "thalach", "exang", "oldpeak", "slope", "ca", "thal", "target"]
df=pd.read_csv(url, names=column_names, na_values="?")
print(df.head())
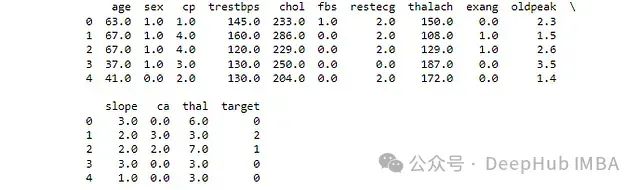
数据预处理
在进行建模之前,我们需要对数据进行预处理:
fromsklearn.imputeimportSimpleImputer
fromsklearn.preprocessingimportLabelEncoder
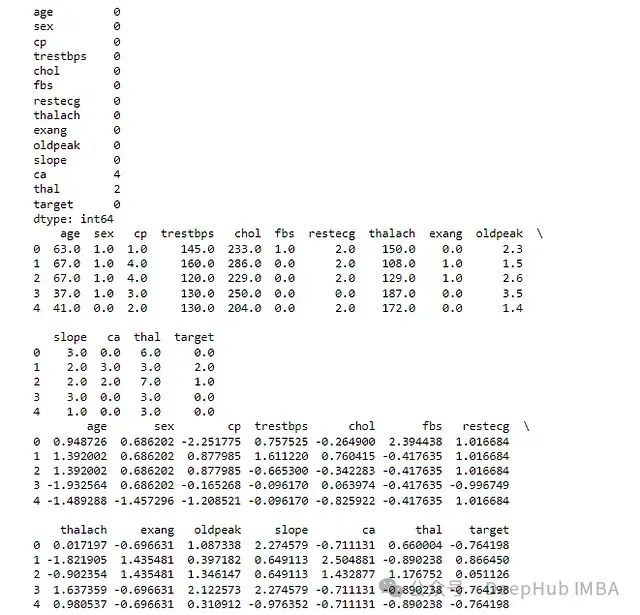
print(df.isnull().sum())
imputer=SimpleImputer(strategy='median')
df_filled=pd.DataFrame(imputer.fit_transform(df), columns=df.columns)
print(df_filled.head())
categorical_vars=df_filled.select_dtypes(include='object').columns
encoder=LabelEncoder()
forvarincategorical_vars:
df_filled[var] =encoder.fit_transform(df_filled[var])
scaler=StandardScaler()
df_normalized=pd.DataFrame(scaler.fit_transform(df_filled), columns=df_filled.columns)
print(df_normalized.head())
基准模型
我们首先建立一个基准逻辑回归模型:
fromsklearn.model_selectionimporttrain_test_split
fromsklearn.linear_modelimportLogisticRegression
fromsklearn.metricsimportaccuracy_score, roc_auc_score
df_normalized['target'] =df['target']
df_normalized['target'] =df_normalized['target'].apply(lambdax: 1ifx>0else0)
X=df_normalized.drop('target', axis=1)
y=df_normalized['target']
X_train, X_test, y_train, y_test=train_test_split(X, y, test_size=0.2, random_state=42)
model=LogisticRegression()
model.fit(X_train, y_train)
y_pred=model.predict(X_test)
accuracy=accuracy_score(y_test, y_pred)
roc_auc=roc_auc_score(y_test, y_pred)
print("Baseline Model "+f'Accuracy: {accuracy}')
print("Baseline Model "+f'ROC-AUC: {roc_auc}')

使用网格搜索进行超参数调优
然后使用网格搜索方法进行超参数调优:
fromsklearn.model_selectionimportGridSearchCV
hyperparameters= {'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000],
'penalty': ['l1', 'l2']}
grid_search=GridSearchCV(LogisticRegression(), hyperparameters, cv=5, scoring='roc_auc')
grid_search.fit(X_train, y_train)
best_params=grid_search.best_params_
print(f'Best hyperparameters: {best_params}')
best_model=grid_search.best_estimator_
y_pred_best=best_model.predict(X_test)
accuracy_best=accuracy_score(y_test, y_pred_best)
roc_auc_best=roc_auc_score(y_test, y_pred_best)
print("Grid Search Method "+f'Accuracy of the best model: {accuracy_best}')
print("Grid Search Method "+f'ROC-AUC of the best model: {roc_auc_best}')

使用蒙特卡洛方法进行超参数调优
最后应用蒙特卡洛方法进行超参数调优:
fromsklearn.metricsimportaccuracy_score, roc_auc_score
fromsklearn.linear_modelimportLogisticRegression
fromsklearn.model_selectionimporttrain_test_split
importnumpyasnp
X_train, X_test, y_train, y_test=train_test_split(X, y, test_size=0.2, random_state=42)
C_range=np.logspace(-3, 3, 7)
penalty_options= ['l1', 'l2']
best_score=0
best_hyperparams=None
for_inrange(1000):
C=np.random.choice(C_range)
penalty=np.random.choice(penalty_options)
model=LogisticRegression(C=C, penalty=penalty, solver='liblinear')
model.fit(X_train, y_train)
y_pred=model.predict(X_test)
accuracy=accuracy_score(y_test, y_pred)
roc_auc=roc_auc_score(y_test, y_pred)
ifroc_auc>best_score:
best_score=roc_auc
best_hyperparams= {'C': C, 'penalty': penalty}
print("Monte Carlo Method "+f'Best ROC-AUC: {best_score}')
print("Monte Carlo Method "+f'Best hyperparameters: {best_hyperparams}')
best_model=LogisticRegression(**best_hyperparams, solver='liblinear')
best_model.fit(X_train, y_train)
y_pred=best_model.predict(X_test)
accuracy=accuracy_score(y_test, y_pred)
print("Monte Carlo Method "+f'Accuracy of the best model: {accuracy}')

网格搜索与蒙特卡洛方法的比较
网格搜索方法通过评估超参数空间中所有可能组合的性能来选择"最佳"超参数。它使用交叉验证来评估每种组合在训练数据的不同子集上的平均性能。这种方法可以系统地探索整个超参数空间,但当超参数数量增加时,计算成本会急剧上升。
相比之下,蒙特卡洛方法随机采样超参数空间,并在整个训练集上评估模型性能。这种方法不使用交叉验证,因此可能更容易受到过拟合的影响。但是它能够更快地探索大型超参数空间,并且在计算资源有限的情况下可能更为实用。
在这个实验中蒙特卡洛方法的性能略优于网格搜索方法。这可能是因为蒙特卡洛方法能够探索更广泛的超参数组合,而不受预定义网格的限制。但是需要注意的是,这种性能差异可能因数据集和问题的不同而变化。
总结
蒙特卡洛方法源于一个简单的概率问题,已经发展成为解决复杂计算和优化问题的强大工具。在机器学习领域,特别是在超参数调优方面,蒙特卡洛方法展现出了其独特的优势。
通过本文的分析和实验,我们看到蒙特卡洛方法在估算π值和优化机器学习模型超参数等任务中的应用。这种方法的强大之处在于其能够有效地处理高维度、非线性的问题空间,为我们提供了一种在复杂系统中做出决策的有力工具。
然而,值得注意的是,蒙特卡洛方法并非万能的。在某些情况下,其他方法如网格搜索或贝叶斯优化可能更为适合。选择最佳方法应该基于具体问题、可用的计算资源以及对精度和效率的需求。