图卷积网络（Graph Convolution Network，GCN）

一、前言

在图神经网络出现之前，一般的神经网络只能对常规的欧式数据进行处理，其特点就是节点有固定的排列规则和顺序，如２维网格和１维序列。

近几年来，将深度学习应用到处理和图结构数据相关的任务中越来越受到人们的关注。图神经网络的出现使其在上述任务中取得了重大突破，比如在社交网络、自然语言处理、计算机视觉甚至生命科学等领域得到了非常广泛的应用。图神经网络可以把实际问题看作图中节点之间的连接和消息传播问题，对节点之间的依赖关系进行建模，从而能够很好地处理图结构数据。

近年来，CNN在图像识别、自然语言处理等多个领域应用广泛，但其只能高效地处理网格和序列等这样规则的欧氏数据，不能有效地处理像社交多媒体网络数据、化学成分结构数据、生物蛋白数据以及知识图谱数据等图结构的非欧氏数据。因为图的结构一般是极为不规则的，每一个节点的周围结构可能都是独一无二的，其邻居节点和连接的边各不相同，所以传统的CNN难以处理这类图结构数据。图卷积神经网络（Graph Convolution Network，GCN）是CNN在图结构的非欧氏数据上的应用，GCN 是图神经网络中一个重要分支，现有的大多数图算法模型基本上都是在GCN基础上变化推导而来。

二、GCN原理

对于一个图结构数据集 $G$ ，其中有 $N$ 个节点（node），每个节点都有自己的特征，我们设这些节点的特征组成一个 $N*D$ 大小的矩阵 $X$ ， $D$ 表示每个节点隐藏状态维度。另外各个节点之间的关系也可以提取为一个 $N*N$ 大小的关系矩阵 $A$ ，也称为邻接矩阵（adjacency matrix）。 $X$ 和 $A$ 就是GCN模型中输入的特征。

$X$ 表示节点特征，每个节点都具有自己的向量表示; $A$ 表示图结构特征，即节点与节点间的边的信息。

一个基于分层传播规则的 $L$ 层GCN，其层与层之间的传播方式为：

$H^{(l+1)}=\sigma (\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})$

其中：

$\tilde{A}=A+I_{N}$ ， $I_{N}$ 是一个 $N$ 维的单位矩阵。之所以要加上一个单位矩阵，是因为邻接矩阵 $A$ 的对角线上都是0（节点不存在self-loop关系），所以在和特征矩阵 $H$ 相乘时会忽略该节点自身的特征。而给 $A$ 加上一个单位矩阵 $I_{N}$ 就使得对角线元素变成1。

$\tilde{D}$ 是 $\tilde{A}$ 的度矩阵（degree matrix），公式为： $\tilde{D}_{ii}={\sum}_{j}\tilde{A}_{ij}$ 。 $\tilde{A}$ 是没有经过归一化的矩阵，若与 $H$ 直接相乘会改变特征原本的分布。因为不同节点，其边的数量和权值都不一样，有的节点连接了多条边，这导致具有多条边的节点在聚合后的特征值远大于具有较少边的节点。所以需要对 $\tilde{A}$ 进行标准化处理，使 $\tilde{A}$ 的每一行加起来为1， $\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}$ 是对称且归一化的矩阵。

$W^{(l)}$ 是 $l$ 层的权重矩阵。

$\sigma (\cdot )$ 表示非线性激活函数，如ReLU函数。

$H^{(l)}\in \mathbb{R}^{N*D}$ 为第 $l$ 层的激活矩阵， $H^{(0)}=X$ ， $H^{(L)}=Z$ 。

GCN的层（layers）：

GCN的层数 $L$ 是指节点特征能够传播的最远距离。例如，在1层的GCN中，每个节点只能从其邻居那里获得信息。每个节点收集信息的过程是独立进行的，但对所有节点来说是在同一时间进行的。

当在第一层的基础上再叠加一层时，即重复聚合信息的过程，但这一次，邻居节点已经有了自己的邻居的信息（来自上一步），这使得层数成为每个节点可以走的最大跳步。但GCN作者通过实验表明，GCN层数不宜多，2-3层就足够了，过多的层数反而会适得其反。

三、GCN用于节点分类

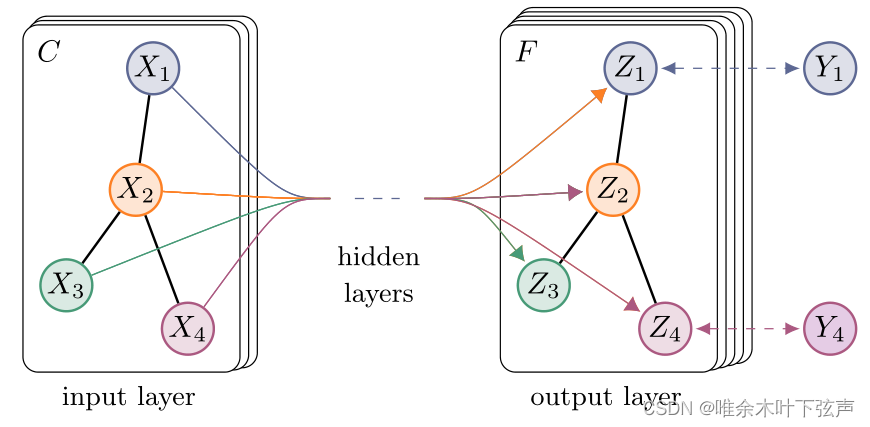上图中的GCN输入一个图，通过 $L$ 层GCN后每个节点的特征从 $X$ 变成了 $Z$ 。 $Y$ 表示节点的标签。

假设我们构造一个两层的GCN，激活函数分别采用ReLU和Softmax，则整体的正向传播的公式为：

$Z=f(X,A)=softmax(\hat{A}ReLU(\hat{A}XW^{(0)})W^{(1)})$

其中， $\hat{A}=\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}$ 。

然后，针对所有带标签的节点计算cross entropy损失函数：

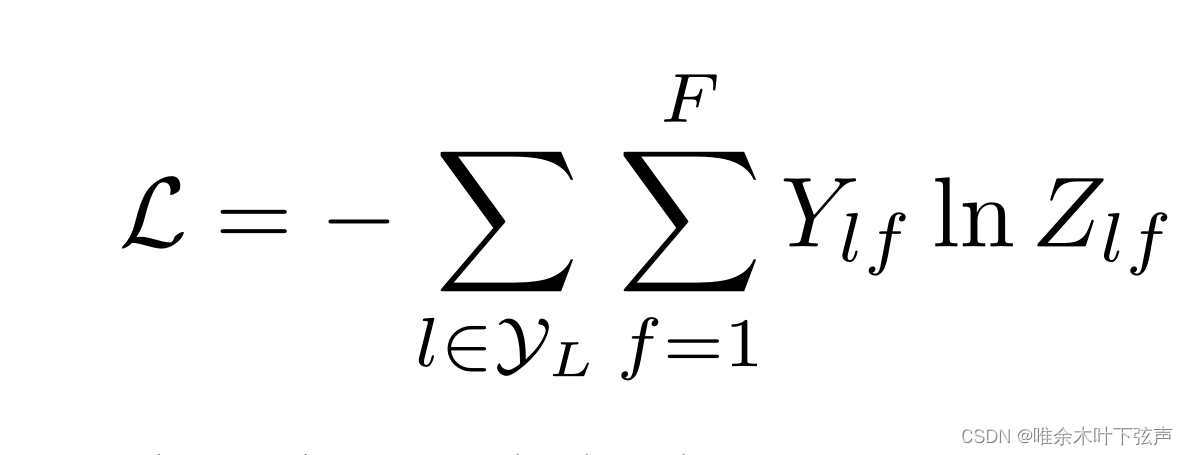
这样就可以训练一个用于节点分类的GCN模型了，即使只有很少节点带有标签也能训练，作者称他们的方法为半监督分类（Semi-Supervised node classification）。除此之外，将损失函数变动一下，GCN也可以用来做链接预测等任务。

四、总结

GCN的提出在图任务处理领域具有里程碑式的意义，原作者的实验表明，即使使用随机初始化的参数 $W$ ，GCN提取出来的节点特征就很好了，其聚类结果比得上DeepWalk、node2vec算法经过复杂训练后得到节点特征的效果。

GCN其实是拉普拉斯平滑的特殊形式，GCN的主要思想是取所有邻居节点特征（包括自身节点）的加权平均值。度低的节点获得更大的权重，然后将得到的特征向量通过神经网络进行训练。在GCN中，节点特征的更新是靠不断聚合邻居节点特征实现的，这会使得相邻节点的相似性增强，从而使分类能力大大增强。但如果堆叠多层GCN网络，输出特征可能过度平滑，使来自不同簇的顶点可能变得不可区分，分类效果也就会下降。

另外，对于更复杂的图，如异构图、动态图、带权重的图，GCN还不能有效应对。对于含有大规模数量节点和边的图，也给GCN的计算带来挑战。在GCN提出之后，有不少工作针对其不足之处做出了改进，如R-GCN、GraphSAGE等模型。

参考文献：

1、Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.

2、何时能懂你的心——图卷积神经网络（GCN） - 知乎

3、GCN图卷积网络入门详解

标签：深度学习人工智能

本文转载自: https://blog.csdn.net/weixin_44458771/article/details/129040246
版权归原作者 唯余木叶下弦声 所有，如有侵权，请联系我们删除。

图卷积网络（Graph Convolution Network，GCN）

一、前言

二、GCN原理

三、GCN用于节点分类

四、总结

发表评论

“图卷积网络（Graph Convolution Network，GCN）”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航