Pytorch+PyG实现MLP

文章目录

前言

大家好，我是阿光。

本专栏整理了《图神经网络代码实战》，内包含了不同图神经网络的相关代码实现（PyG以及自实现），理论与实践相结合，如GCN、GAT、GraphSAGE等经典图网络，每一个代码实例都附带有完整的代码。

正在更新中~ ✨

🚨 我的项目环境：

• 平台：Windows10
• 语言环境：python3.7
• 编译器：PyCharm
• PyTorch版本：1.11.0
• PyG版本：2.1.0

💥 项目专栏：【图神经网络代码实战目录】

本文我们将使用Pytorch + Pytorch Geometric来简易实现一个MLP（感知机网络），让新手可以理解如何PyG来搭建一个简易的图网络实例demo。

一、导入相关库

本项目我们需要结合两个库，一个是Pytorch，因为还需要按照torch的网络搭建模型进行书写，第二个是PyG，因为在torch中并没有关于图网络层的定义，所以需要torch_geometric这个库来定义一些图层。

import torch
import torch.nn.functional as F
import torch.nn as nn
import torch_geometric.nn as pyg_nn
from torch_geometric.datasets import Planetoid

二、加载Cora数据集

本文使用的数据集是比较经典的Cora数据集，它是一个根据科学论文之间相互引用关系而构建的Graph数据集合，论文分为7类，共2708篇。

• Genetic_Algorithms
• Neural_Networks
• Probabilistic_Methods
• Reinforcement_Learning
• Rule_Learning
• Theory

这个数据集是一个用于图节点分类的任务，数据集中只有一张图，这张图中含有2708个节点，10556条边，每个节点的特征维度为1433。

# 1.加载Cora数据集
dataset = Planetoid(root='./data/Cora', name='Cora')

三、定义MLP网络

这里我们就不重点介绍MLP网络了，相信大家能够掌握基本原理，本文我们使用的是PyG定义网络层，在PyG中已经定义好了MLP这个层，该层采用的就是感知机机制。

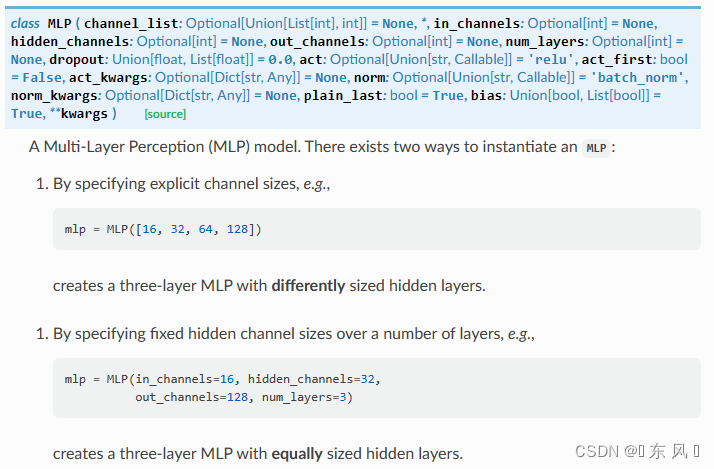
对于MLP的常用参数：

• channel_list：样本输入层、中间层、输出层维度的列表
• in_channels：每个样本的输入维度，就是每个节点的特征维度
• hidden_channels：单层神经网络中间的隐层大小
• out_channels：经过MLP后映射成的新的维度，就是经过MLP后每个节点的维度长度
• num_layers：感知机层数
• dropout：每个隐藏层的丢弃率，如果存在多层可以使用列表传入
• act：激活函数，默认为relu
• bias：训练一个偏置b

对于本文实现的

pyg_nn.MLP([num_node_features, 32, 64, 128])

的含义就是定义一个三层的感知机网络，按照

PyTorch

实现等价于如下代码：

lin_1 = nn.Linear(num_node_features,32)
lin_2 = nn.Linear(32,64)
lin_3 = nn.Linear(64,128)

对于

PyG

中实现起来较为简单，以列表方式传入所以隐层大小即可，第一个维度代表样本的输入特征维度，最后一个维度代表输出的维度大小，中间维度代表隐层的大小，所以

len(channel_list) - 1

代表

MLP

的层数，这种方式是以传入

channel_list

方式定义模型，还可以按照正常参数方式进行传递定义，代码如下：

pyg_nn.MLP(in_channels=16,
           hidden_channels=32,
           out_channels=128,
           num_layers=3)

网络定义代码如下：

# 2.定义MLP网络classMLP(nn.Module):def__init__(self, num_node_features, num_classes):super(MLP, self).__init__()
        self.lin_1 = pyg_nn.MLP([num_node_features,32,64,128])
        self.lin_2 = pyg_nn.MLP([128,64,32, num_classes])defforward(self, data):
        x, edge_index = data.x, data.edge_index
        
        x = self.lin_1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.lin_2(x, edge_index)return F.log_softmax(x, dim=1)

上面网络我们定义了两个MLP层，第一层的参数的输入维度就是初始每个节点的特征维度，输出维度是128。

第二个层的输入维度为128，输出维度为分类个数，因为我们需要对每个节点进行分类，最终加上softmax操作。

四、定义模型

下面就是定义了一些模型需要的参数，像学习率、迭代次数这些超参数，然后是模型的定义以及优化器及损失函数的定义，和pytorch定义网络是一样的。

device = torch.device('cuda'if torch.cuda.is_available()else'cpu')# 设备
epochs =10# 学习轮数
lr =0.003# 学习率
num_node_features = dataset.num_node_features # 每个节点的特征数
num_classes = dataset.num_classes # 每个节点的类别数
data = dataset[0].to(device)# Cora的一张图# 3.定义模型
model = MLP(num_node_features, num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=lr)# 优化器
loss_function = nn.NLLLoss()# 损失函数

五、模型训练

模型训练部分也是和pytorch定义网络一样，因为都是需要经过前向传播、反向传播这些过程，对于损失、精度这些指标可以自己添加。

# 训练模式
model.train()for epoch inrange(epochs):
    optimizer.zero_grad()
    pred = model(data)
    
    loss = loss_function(pred[data.train_mask], data.y[data.train_mask])# 损失
    correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item()# epoch正确分类数目
    acc_train = correct_count_train / data.train_mask.sum().item()# epoch训练精度
    
    loss.backward()
    optimizer.step()if epoch %20==0:print("【EPOCH: 】%s"%str(epoch +1))print('训练损失为：{:.4f}'.format(loss.item()),'训练精度为：{:.4f}'.format(acc_train))print('【Finished Training！】')

六、模型验证

下面就是模型验证阶段，在训练时我们是只使用了训练集，测试的时候我们使用的是测试集，注意这和传统网络测试不太一样，在图像分类一些经典任务中，我们是把数据集分成了两份，分别是训练集、测试集，但是在Cora这个数据集中并没有这样，它区分训练集还是测试集使用的是掩码机制，就是定义了一个和节点长度相同纬度的数组，该数组的每个位置为True或者False，标记着是否使用该节点的数据进行训练。

# 模型验证
model.eval()
pred = model(data)# 训练集（使用了掩码）
correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item()
acc_train = correct_count_train / data.train_mask.sum().item()
loss_train = loss_function(pred[data.train_mask], data.y[data.train_mask]).item()# 测试集
correct_count_test = pred.argmax(axis=1)[data.test_mask].eq(data.y[data.test_mask]).sum().item()
acc_test = correct_count_test / data.test_mask.sum().item()
loss_test = loss_function(pred[data.test_mask], data.y[data.test_mask]).item()print('Train Accuracy: {:.4f}'.format(acc_train),'Train Loss: {:.4f}'.format(loss_train))print('Test  Accuracy: {:.4f}'.format(acc_test),'Test  Loss: {:.4f}'.format(loss_test))

七、结果

【EPOCH: 】1
训练损失为：1.9856 训练精度为：0.1786
【EPOCH: 】21
训练损失为：1.5419 训练精度为：0.4643
【EPOCH: 】41
训练损失为：1.1653 训练精度为：0.6500
【EPOCH: 】61
训练损失为：0.8062 训练精度为：0.8071
【EPOCH: 】81
训练损失为：0.5322 训练精度为：0.9286
【EPOCH: 】101
训练损失为：0.3487 训练精度为：0.9714
【EPOCH: 】121
训练损失为：0.2132 训练精度为：0.9571
【EPOCH: 】141
训练损失为：0.1043 训练精度为：0.9929
【EPOCH: 】161
训练损失为：0.0601 训练精度为：1.0000
【EPOCH: 】181
训练损失为：0.0420 训练精度为：1.0000
【Finished Training！】

>>>Train Accuracy:1.0000 Train Loss:0.0092>>>Test  Accuracy:0.1800 Test  Loss:1.9587

训练集测试集Accuracy1.00000.1800Loss0.00921.9587

完整代码

import torch
import torch.nn.functional as F
import torch.nn as nn
import torch_geometric.nn as pyg_nn
from torch_geometric.datasets import Planetoid

# 1.加载Cora数据集
dataset = Planetoid(root='./data/Cora', name='Cora')# 2.定义MLP网络classMLP(nn.Module):def__init__(self, num_node_features, num_classes):super(MLP, self).__init__()
        self.lin_1 = pyg_nn.MLP([num_node_features,32,64,128])
        self.lin_2 = pyg_nn.MLP([128,64,32, num_classes])defforward(self, data):
        x, edge_index = data.x, data.edge_index
        
        x = self.lin_1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.lin_2(x, edge_index)return F.log_softmax(x, dim=1)

device = torch.device('cuda'if torch.cuda.is_available()else'cpu')# 设备
epochs =200# 学习轮数
lr =0.0003# 学习率
num_node_features = dataset.num_node_features # 每个节点的特征数
num_classes = dataset.num_classes # 每个节点的类别数
data = dataset[0].to(device)# Cora的一张图# 3.定义模型
model = MLP(num_node_features, num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=lr)# 优化器
loss_function = nn.NLLLoss()# 损失函数# 训练模式
model.train()for epoch inrange(epochs):
    optimizer.zero_grad()
    pred = model(data)
    
    loss = loss_function(pred[data.train_mask], data.y[data.train_mask])# 损失
    correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item()# epoch正确分类数目
    acc_train = correct_count_train / data.train_mask.sum().item()# epoch训练精度
    
    loss.backward()
    optimizer.step()if epoch %20==0:print("【EPOCH: 】%s"%str(epoch +1))print('训练损失为：{:.4f}'.format(loss.item()),'训练精度为：{:.4f}'.format(acc_train))print('【Finished Training！】')# 模型验证
model.eval()
pred = model(data)# 训练集（使用了掩码）
correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item()
acc_train = correct_count_train / data.train_mask.sum().item()
loss_train = loss_function(pred[data.train_mask], data.y[data.train_mask]).item()# 测试集
correct_count_test = pred.argmax(axis=1)[data.test_mask].eq(data.y[data.test_mask]).sum().item()
acc_test = correct_count_test / data.test_mask.sum().item()
loss_test = loss_function(pred[data.test_mask], data.y[data.test_mask]).item()print('Train Accuracy: {:.4f}'.format(acc_train),'Train Loss: {:.4f}'.format(loss_train))print('Test  Accuracy: {:.4f}'.format(acc_test),'Test  Loss: {:.4f}'.format(loss_test))