一、训练加速
针对训练数据过于庞大的对策,多GPU训练,加速生产模型的速度,可以认为是离线操作。
常用的GPU训练:
- 基于数据的并行(常用)
- 基于模型的并行
我们主要看一下基于数据的并行,下面列出了三种并行方式
①Model Average(模型平均)
②SSGD(同步随机梯度下降)
③**ASGD*(异步随机梯度下降)**
1.基于数据的并行
①Model Average(模型平均)
假设有10000条数据,分成10份,每份1000条,用十个GPU分别训练,最后将得到的模型进行平均。这样训练出来的模型之间是相互独立的,故性能不会很好。
而我们希望任务在训练过程中是保持通信的,可以怎么样做呢?
如下图所示,我们将10000条数据分配到10 个Client,每个Client处理分别1000条数据。这十个Client都有一个共享的初始模型W0。我们设置batch=100,每个Client运行一个batch后,都会更新一个模型W1。此时这10个Client的初始化模型W0是一样的,W1是不一样的,因为其输入的数据不一样。这样我们把10个Client的模型W1都发送给Server,Server对接受到的10个W1进行平均(这个过程就是模型平均),这样就得到了一个新的W1,然后再将这个新的W1分别发送给10个Client,每个Client都会接收到一个新的W1,并覆盖掉原来的W1,这样,这10个Client的W1就是一样的了。进行第二个batch得到W2。。。。
需要注意的是,在运行一个batch的过程中,可能有的Client的GPU更好,其模型W先于其他几个Client计算出来,虽然他计算的快,但他仍然要等其他几个Client的W都计算出来之后,再同步的发送给Server,整个网络训练速度取决于最慢的Client的计算速度。
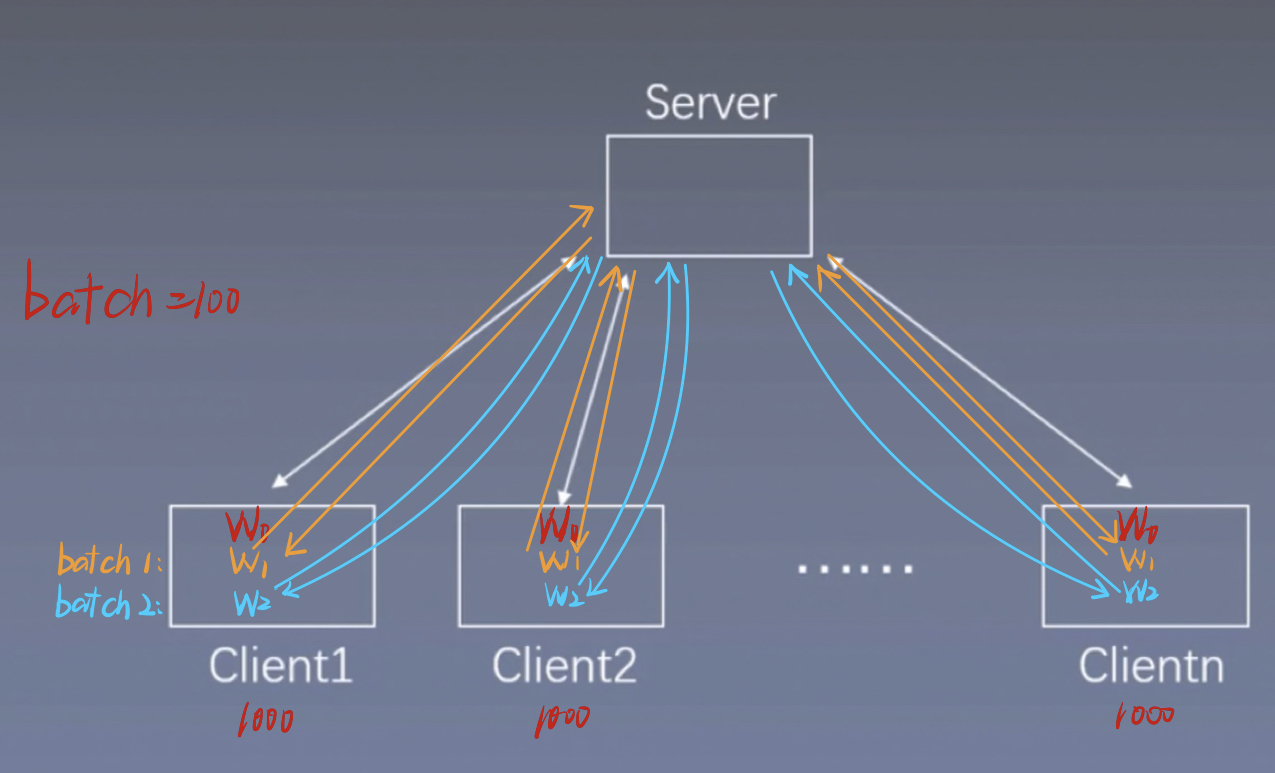
②SSGD(同步随机梯度下降)
如下图所示,我们将10000条数据分配到10 个Client,每个Client处理分别1000条数据。这十个Client都有一个共享的初始模型W0。
同理设置batch=100,运行第一个batch,每个Client进行一次前向后向传播,得出W的梯度,此时这10个Client的是各不相同的,不进行共享的。然后将求得的这十个
同步发送给Server,Server接收到 后,先对这10个
做一个平均,这样就得到了一个新的
,新的
再对W0做一个梯度下降得到W1,然后将这个W1发送给10个Client。
同理,运行第二个batch,将10个Client得出的梯度发送到Server做平均,再将得到的新梯度对W1做梯度下降得到W2,在发送给10个Client。。。。。
该方法也是同步的将梯度发送到Server,整个网络训练速度取决于最慢的Client的计算速度。

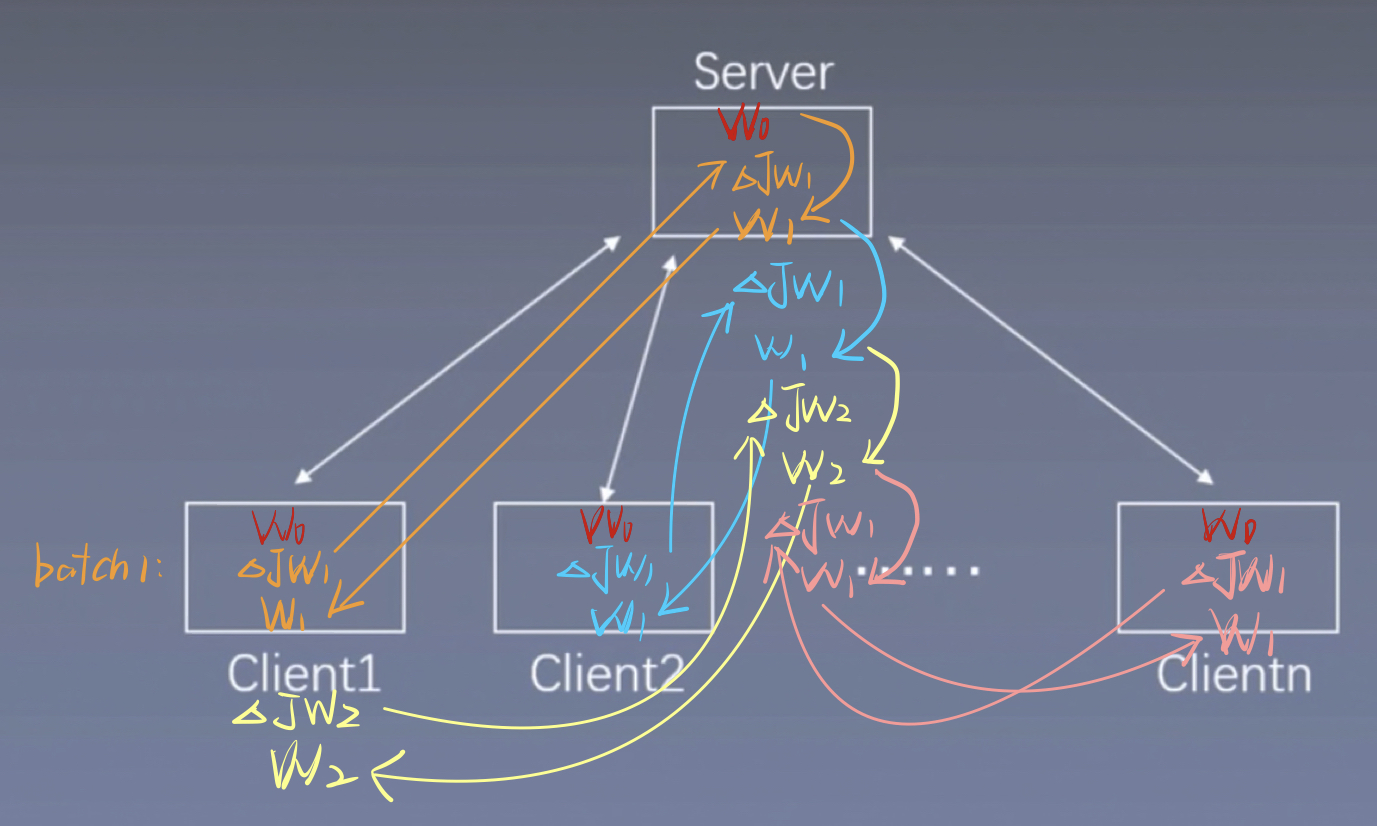
③ASGD*(异步随机梯度下降)
该方法是比较常用的,损失比较小,效率也是最高的。
如下图所示,我们将10000条数据分配到10 个Client,每个Client处理分别1000条数据。这十个Client都有一个共享的初始模型W0。
该方法与SSGD(同步随机梯度下降)相同,都是现在Client端计算完梯度,再发送到Server端计算W1,区别在于本节方法是一个异步的过程,无需等待每个Client的都计算完成,
那他们是怎么进行异步操作的呢?
我们假设Client 1 先计算完第一个batch,并得到,此时Client 1 无需等待其他几个Client完成,只需直接将发送到Server并对Server中的W0做梯度下降,然后得到了W1,Server再将W1模型发送到Client 1 ,然后开始计算第二个batch,当第二个batch进行到一半的时候,Client 2 完成的的计算,Client 2也将求得的传入Server,注意,此时Client 2 传进来的要对最新的W做梯度下降,即对W1做梯度下降,而不是W0,然后将计算出来的W1发送给Client 2。同理,其他Client将梯度发送到Server后,也要对最新的W做梯度更新,注意是最新的,即使Client 1更新了W8,Client 2在Client 1 的基础上更新了W6,后面再进行梯度下降的时候,也要对最新的W6进行计算。
PS:哪个Client最先完成计算,就直接发送给Server,不是按照Client1,2,3,...的顺序。上面那么说只是为了方便描述。
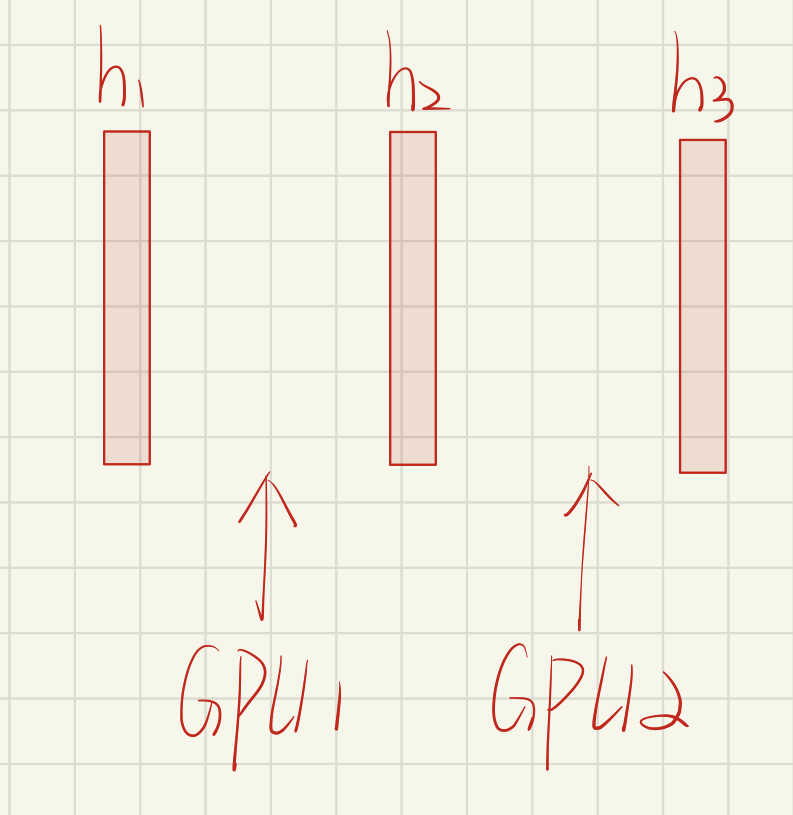
2.基于模型的并行
如下为三个隐藏层,每个GPU负责网络的一部分。
以前向传播为例:
batch 1 ,GPU1 开始运算,GPU2 是空闲的,需要等待GPU1 的结果;GPU1运算完后,开始运行batch2,此时GPU2 拿到GPU1的结果后开始计算,GPU2 计算完后传给GPU3,然后GPU2开始运行batch 2。。。。。
二、推理加速
推理主要是一个前向的过程,将生产的模型运用到线上,主要关心让模型尽可能小。
常见的推理方法如下所示。
1.SVD分解*
将m×n的矩阵分解为三个矩阵相乘
原参数量为m×n,分解后参数量为mk+kn+1

这个结果是怎么来的呢?
我们将上述分解后的矩阵相乘后的多项式如下所示
λ1>λ2>...>λn
我们只去第一项,就可以很大程度的表示A矩阵
所以分解后的参数量为V的参数量mk加U的参数量kn加λ的一个参数共 mk+kn+1。

举个例子:
原矩阵A的参数量为200×100
矩阵分解后200×10+10乘100

为什么要将大模型SVD分解为小模型,而不是直接训练小模型呢?
假设小模型训练的精度为85%,大模型的训练精度可以达到95% ,进行SVD分解后,精度损失,变为了90%,我们再进行微调,精度又有一定的上升,相对于直接训练一个小网络,精度相对要高。
2.Hidden Node prune
将权重较小的节点裁剪掉。
假设一个隐藏层有1000个节点,想剪掉200个节点,那就根据权重进行排序,将权重低的裁剪掉。
同理,为什么不直接训练一个隐藏层800个节点的网络呢?因为隐藏层1000个节点的网络训练效果会更好,裁剪之后性能会有一定的下降,需要再进行微调,精度会有一定提升,精度会高于隐藏层800个节点的网络。
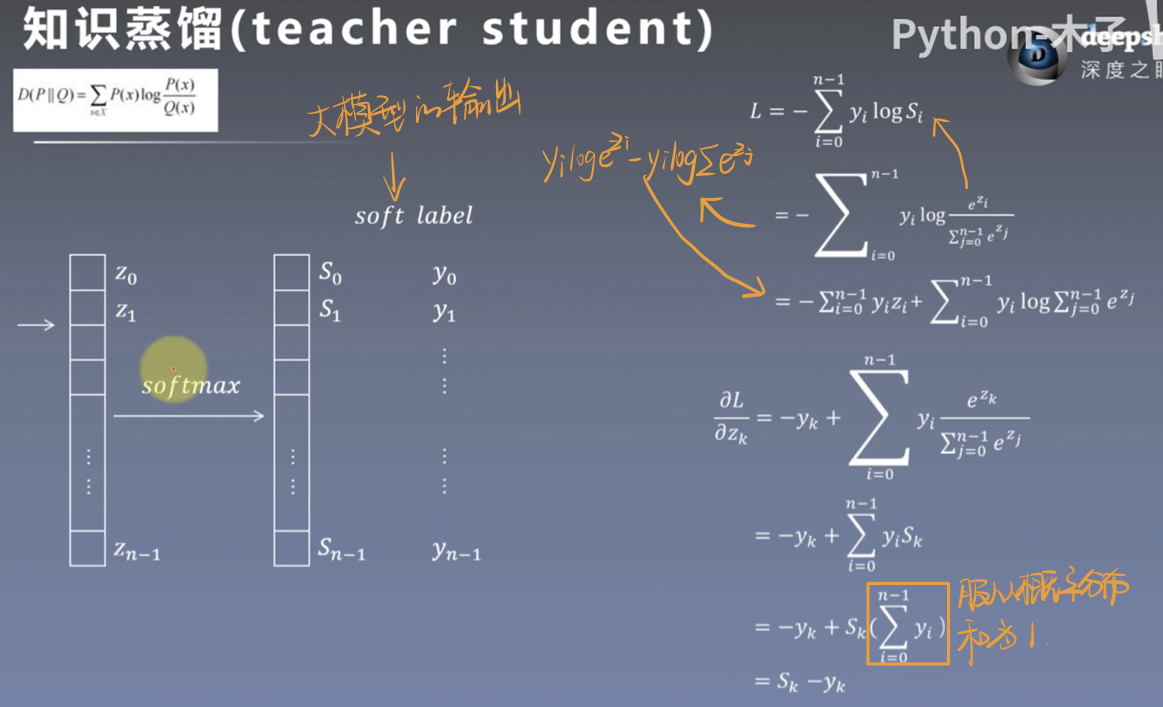
3.知识蒸馏*
知识蒸馏就是先在大网络上进行学习,将学习到的知识迁移到小模型上,训练效果要好于直接训练一个小模型。
我们将带有硬标签(0,0,0,1,0,0)的数据输入到大模型中, 它的输出结果是一个软标签(0.1,0.1,0.9,0.2,0.3)。
假设大模型的结果足够好,我们可以将大模型的输出作为一个标签,该标签为软标签,不仅可以学习到正负样本的特征,也可以学习到正负样本之间的关系,富含更多信息,更有助于小模型的学习。
例如:一张图片中有三个物体,熊猫、狗、飞机,我们期望检测到熊猫,该图片的标签为(1,0,0),经过大模型的训练后,输出的标签为(0.99,0.01,0.0005),我们可以看到,狗相对于飞机,与熊猫更接近,故权值也会更大。

对大模型的softmax前一层计算梯度,该梯度会用到小模型的梯度中。
4.参数共享
CNN中的参数共享:一个卷积层中可以有多个不同的卷积核,而每一个卷积核都对应着一个滤波后映射出的新图像(Feature map),同一个新图像的所有像素全部来自于同一个卷积核,这就是卷积核的参数共享。
LSTM中的参数共享:输入x到遗忘门、输入门、输出门和细胞单元,不进行参数共享则需要4×m×n个参数,进行参数共享则只需要m×n个参数。其中m和n分别为输入x和f,i,o,c门的维度。
5.神经网络的量化*
量化就是将浮点运算转换成整数运算。
浮点计算非常耗时,而转换成整数后,计算量就会明显降低。
如w1,w2为32位的浮点数,w'1,w'2为转换后的8位的整数。
两个8位的整数相乘w'1×w'2要比两个32位的浮点相乘w1×w2速度更快。

6.Binary Net
使用二值网络进行量化
原浮点需要32bit存储,现只用1bit存储。
参数只有-1,1两个参数。
采用位运算进行加速。
训练时候前向后向传播算法的微调。
7.基于fft的循环矩阵加速
网络中一般需要多次矩阵相乘,但是矩阵相乘是非常耗时的
那怎么办呢?
我们将矩阵C变为循环矩阵W
这样原来矩阵C与x相乘就变为了W与x相乘,该结果就像两个向量的卷积计算,求完积和后,向后移一位,再进行计算,即c与x的卷积运算。
我们将卷积c*x进行傅里叶变换,它等价于傅里叶变换(f f t)的乘积。我们再对两个傅里叶乘积进行傅里叶逆运算,就得到了c*x的结果,这样就进行了三次傅里叶变换,其计算速度要高于矩阵c与x的计算速度。该操作如下所示。

傅里叶变换的操作是非常快的。

三、深度学习自适应
1.初始参数的网络迁移
用已有数据集如ImageNet先训练一个模型,在新数据上以此模型作为初始模型做fine tuning。
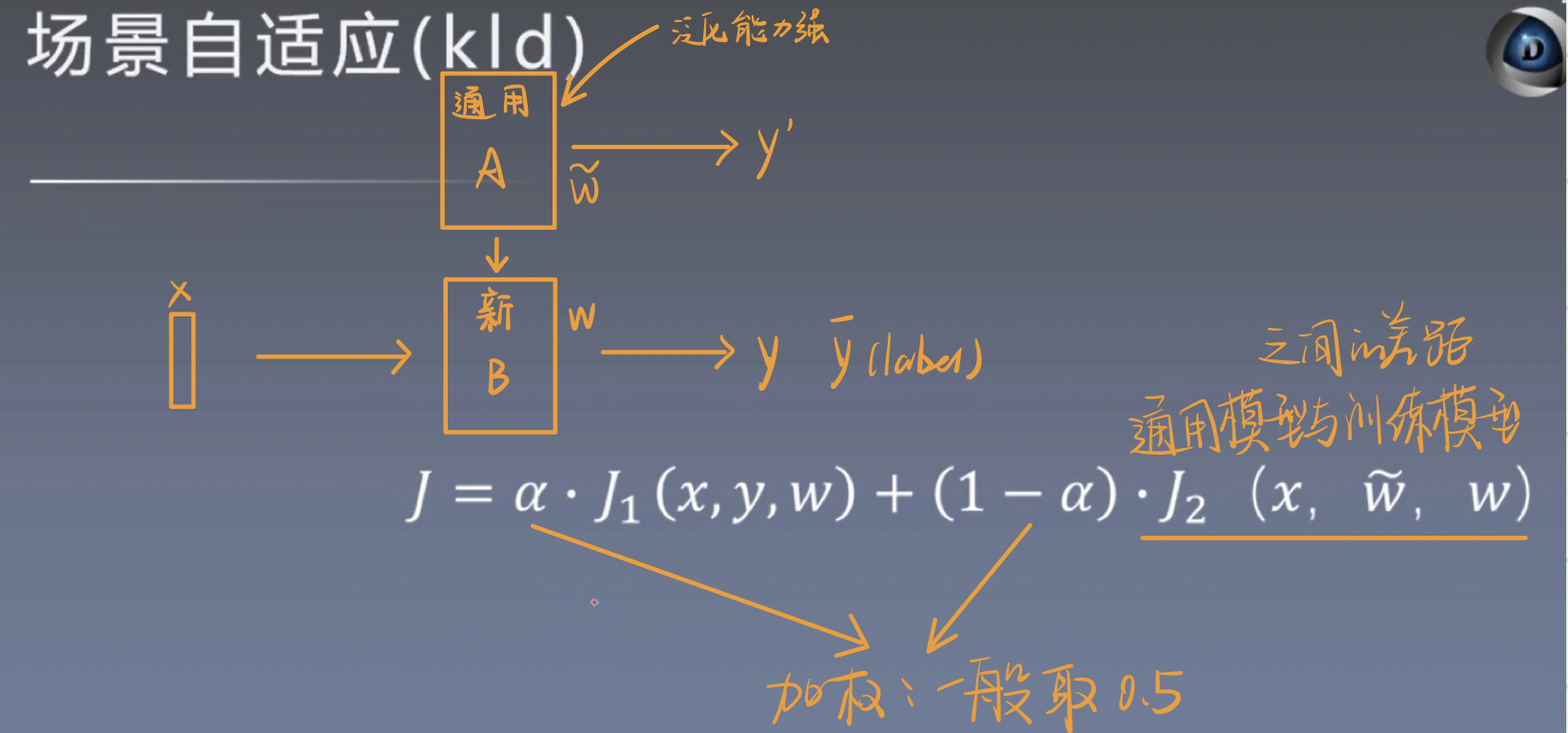
2.场景自适应(KLD)
3.数据的混合
①新增数据量比较大
原始数据量比较大,有几百万条,新增的数据约20万左右,则可以直接将新增的数据均匀的插入到原始数据中。
效果会好一些,缺点是训练慢。
②新增数据量比较小
如果原始数据比较大,有几百万,新增的数据量比较小,几千条,直接混合可能对模型精度影响比较小,所以可以对原始数据中的后一部分(约十万左右)进行混合,则在训练后期,新数据的影响会比较大。
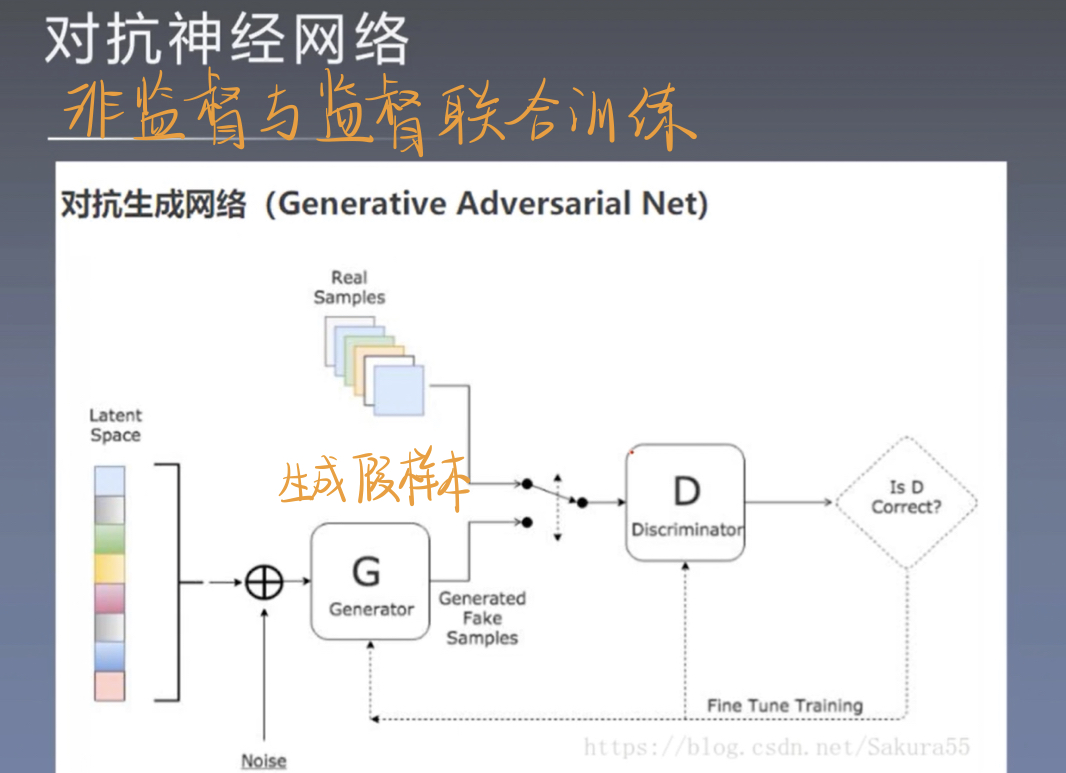
四、对抗神经网络

版权归原作者 Billie使劲学 所有, 如有侵权,请联系我们删除。