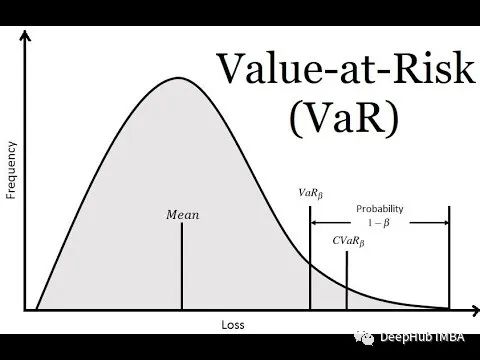
风险价值(VaR)是金融领域广泛使用的风险度量,它量化了在特定时间范围内和给定置信度水平下投资或投资组合的潜在损失。它提供了一个单一的数字,代表投资者在正常市场条件下可能经历的最大损失。VaR是风险管理、投资组合优化和法规遵从的重要工具。
在本文中我们将介绍VaR的概念,并使用Python计算它,然后实现不同的VaR计算方法,最后使用真实的数据来演示计算并将结果可视化。
风险价值
风险价值(VaR)是一种统计度量,用于在特定的时间范围和给定的置信度水平上估计投资或投资组合的潜在损失。它提供了一种量化投资的下行风险的方法,并帮助投资者在风险管理和投资组合分配方面做出明智的决策。
VaR通常以负的金额表示,代表投资者在一定程度的信心下可以预期经历的最大损失。例如,在95%的置信水平下,值为100万美元意味着在指定的时间范围内有5%的可能性损失超过100万美元。
有几种计算VaR的方法,每种方法都有自己的假设和局限性。在本文中,我们将探讨三种常用的VaR计算方法:历史模拟法、参数化法、蒙特卡洛模拟法
需要注意的是:VAR并不提供关于损失超过这个值的情况下可能面临的实际损失的信息。因此,在使用VAR时还需要结合其他风险度量指标和情景分析,来更全面地了解潜在风险。
历史模拟方法
历史模拟法是一种非参数方法,它使用历史价格数据来估计投资或投资组合的潜在损失。它假设未来收益将遵循与过去收益相同的分布,并根据收益的历史分布计算VaR。
为了计算历史VaR,我们需要一个资产或投资组合的历史价格的时间序列。这里使用yfinance库获得这些数据,它允许我们下载真实资产的财务数据。
安装yfinance开始:
pip install yfinance
我们导入必要的库并下载特定资产的历史价格数据。本文将使用摩根大通公司(JPM) 2010年1月1日至2023年10月31日的股价数据。
import yfinance as yf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Download historical price data
data = yf.download("JPM", start="2010-01-01", end="2023-10-31")
现在有了历史价格数据,就可以计算日收益了。每日收益是按一天到第二天价格变化的百分比计算的。
# Calculate daily returns
data["Returns"] = data["Close"].pct_change()
下一步使用使用历史收益来计算VaR。特定置信水平下的VaR是历史收益的第n个百分位数的负值,其中n由置信水平决定。例如,要在95%的置信水平上计算VaR,需要找到5%的历史回报低于该值的值。
# Calculate VaR
confidence_level = 0.95
var = -np.percentile(data["Returns"].dropna(), (1 - confidence_level) * 100)
最后使用直方图来可视化VaR:
# Plot histogram of returns
plt.hist(data["Returns"].dropna(), bins=50, density=True, alpha=0.7)
# Plot VaR line
plt.axvline(x=var, color="red", linestyle="--", linewidth=2)
# Add labels and title
plt.xlabel("Returns")
plt.ylabel("Frequency")
plt.title(f"Historical VaR at {confidence_level * 100}% Confidence Level: {var:.2%}")
# Show the plot
plt.show()
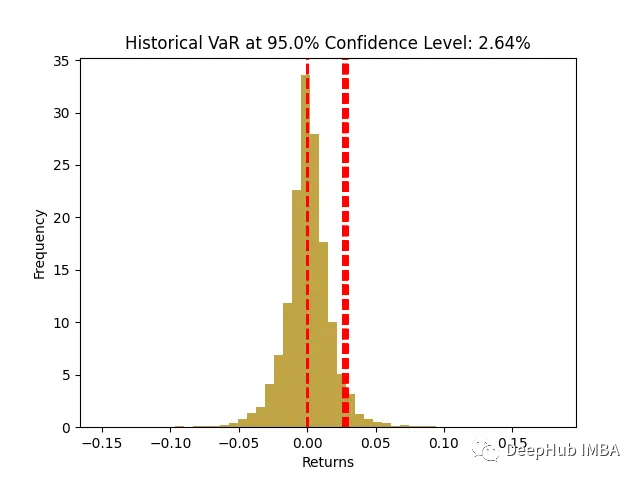
直方图表示日收益分布,红色虚线表示指定置信水平下的VaR。VaR提供了对潜在损失的估计,这种损失在一定程度上是可信的。
参数化法
参数化法是一种假设资产或投资组合的收益遵循特定分布(如正态分布)的方法。它使用统计技术估计分布的参数,并根据这些参数计算VaR。
为了计算参数VaR,需要对收益的分布做出一定的假设。最常见的假设是收益服从正态分布。在这个假设下,我们可以估计收益的均值和标准差,并用它们来计算VaR。
使用与之前相同的摩根大通(JPMorgan Chase & Co.)历史价格数据来计算参数VaR。这里我们假设收益服从正态分布。
# Calculate mean and standard deviation of returns
mean = data["Returns"].mean()
std = data["Returns"].std()
# Calculate VaR
var = -mean - std * np.percentile(np.random.normal(size=10000), (1 - confidence_level) * 100)
使用直方图来可视化
# Plot histogram of returns
plt.hist(data["Returns"].dropna(), bins=50, density=True, alpha=0.7)
# Plot VaR line
plt.axvline(x=var, color="red", linestyle="--", linewidth=2)
# Add labels and title
plt.xlabel("Returns")
plt.ylabel("Frequency")
plt.title(f"Parametric VaR at {confidence_level * 100}% Confidence Level: {var:.2%}")
# Show the plot
plt.show()
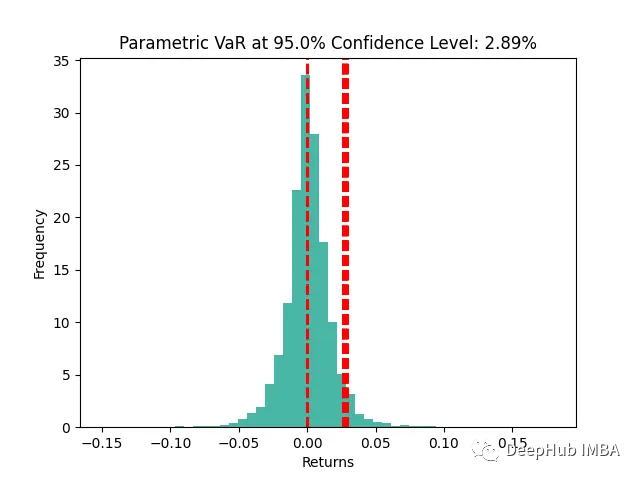
直方图表示日收益分布,红色虚线表示指定置信水平下的VaR。我们假设收益服从正态分布,参数化VaR提供了对具有一定置信度的潜在损失的估计。
蒙特卡洛模拟法
蒙特卡罗模拟法是一种基于模拟的方法,它生成未来收益的多个场景,并根据这些场景计算VaR。它不做任何关于收益分布的假设,可以捕捉非线性关系和复杂的风险因素。
为了计算蒙特卡罗VaR,我们需要根据历史数据模拟未来的回报。我们可以使用历史收益的均值和标准差来生成未来收益的随机情景。
# Set the number of simulations
num_simulations = 10000
# Generate random scenarios of future returns
simulated_returns = np.random.normal(mean, std, size=(len(data), num_simulations))
# Calculate portfolio values for each scenario
portfolio_values = (data["Close"].iloc[-1] * (1 + simulated_returns)).cumprod()
# Convert portfolio_values into a DataFrame
portfolio_values = pd.DataFrame(portfolio_values)
# Calculate portfolio returns for each scenario
portfolio_returns = portfolio_values.pct_change()
# Calculate VaR
if len(portfolio_returns.iloc[-1].dropna()) > 0:
var = -np.percentile(portfolio_returns.iloc[-1].dropna(), (1 - confidence_level) * 100)
else:
var = 0
使用直方图来可视化:
# Plot histogram of portfolio returns
plt.hist(portfolio_returns.iloc[-1].dropna(), bins=50, density=True, alpha=0.7)
# Plot VaR line
plt.axvline(x=var, color="red", linestyle="--", linewidth=2)
# Add labels and title
plt.xlabel("Portfolio Returns")
plt.ylabel("Frequency")
plt.title(f"Monte Carlo VaR at {confidence_level * 100}% Confidence Level: {var:.2%}")
# Show the plot
plt.show()
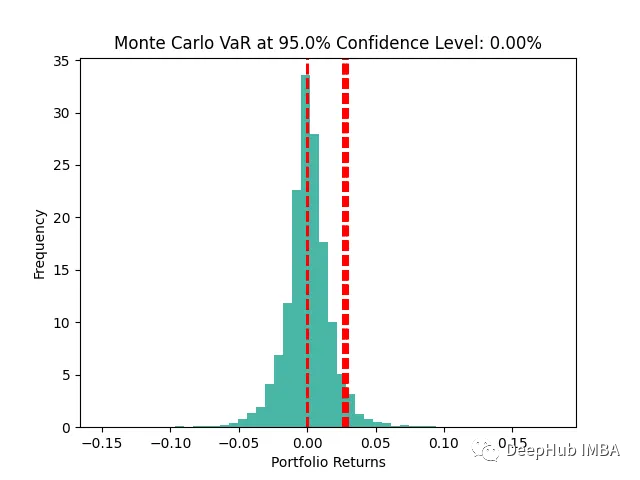
红色虚线表示指定置信水平下的VaR。考虑到非线性关系和复杂的风险因素,蒙特卡洛VaR提供了对具有一定置信度的预期潜在损失的估计。
三种方法对比
我们已经用三种不同的方法计算了VaR,从可视化图表中看不出很大的区别,下面我们来使用数值量化,比较一下三种方法的区别
# Calculate VaR using all three methods
historical_var = -np.percentile(data["Returns"].dropna(), (1 - confidence_level) * 100)
parametric_var = -mean - std * np.percentile(np.random.normal(size=10000), (1 - confidence_level) * 100)
if len(portfolio_returns.iloc[-1].dropna()) > 0:
monte_carlo_var = -np.percentile(portfolio_returns.iloc[-1].dropna(), (1 - confidence_level) * 100)
else:
monte_carlo_var = 0
# Print the VaR values
print(f"Historical VaR: {historical_var:.2%}")
print(f"Parametric VaR: {parametric_var:.2%}")
print(f"Monte Carlo VaR: {monte_carlo_var:.2%}")
结果如下:
Historical VaR: -2.64%
Parametric VaR: -2.84%
Monte Carlo VaR: 0.00%
使用不同方法计算的VaR值略有不同。这是因为每种方法都有不同的假设和近似。在解释VaR结果时,理解每种方法的局限性和假设是很重要的。
总结
本文我们探讨了风险价值(VaR)的概念,并学习了如何使用Python计算它。实现了三种不同的VaR计算方法:历史模拟法、参数化法、蒙特卡洛模拟法。
通过理解和应用VaR,投资者可以在风险管理、投资组合分配和法规遵从方面做出明智的决策。Python为VaR计算提供了一个灵活高效的环境,允许投资者有效地分析和管理风险。
作者:Python Lab