编程，不止有代码，还有艺术

摘要：在代码的世界中，是存在很多艺术般的写法，这可能也是部分程序员追求编程这项事业的内在动力。

本文分享自华为云社区《【云驻共创】用4种代码中的艺术试图唤回你对编程的兴趣》，作者： breakDawn。

也许对于部分人来说，唤起他们编程兴趣的起点可能是一些能快速实现某功能的python小脚本。但作为一个多年的java开发，更多是在接触工作中的业务代码，CURD写久了，总会偶尔感到一丝丝的疲劳。

回望窗外，思索着在代码的世界中，是存在很多艺术般的写法，这可能也是部分程序员追求编程这项事业的内在动力。

这里将为你呈现4种代码中的艺术，试图唤回你对代码最初的兴趣。

设计模式的艺术：用状态模式告别if-else

面对判断分支异常多、状态变化异常复杂的业务逻辑代码，在大量if-else中遨游往往会犯恶心，甚至怀疑起了人生。

例如“手写一个判断函数，确认字符串是否是一个合法的科学数字表达式”这种常见的业务逻辑问题。如果用if-else写，就会变成如下丑陋的代码：

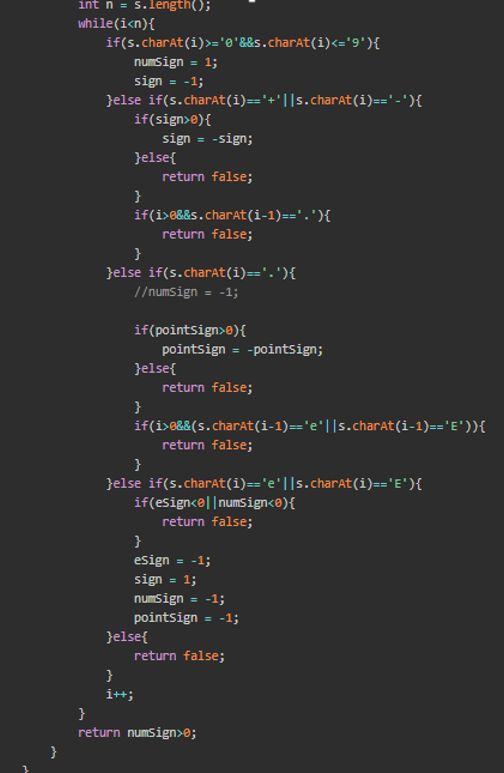
每次维护这种代码，总是都要从头阅读一遍，确认自己要在哪里修改，仿佛在修补一个破旧的大棉袄。

但我们如果使用了设计模式中的状态机模式来进行重构，整块代码就会非常精妙。首先要画出一副如下所示的状态演变图：

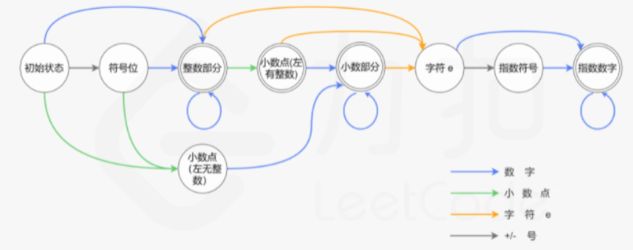
(图源来自leetcode，链接见：https://leetcode.cn/problems/valid-number/solution/you-xiao-shu-zi-by-leetcode-solution-298l/)

状态图绘制完成之后，就可以根据状态变化的合理性，确认状态是否符合要求。

代码如下所示：

class Solution {
        public enum CharType {
            NUMBER,
            OP,
            POINT,
            E;
 
            public static CharType toCharType(Character c) {
                if (Character.isDigit(c)) {
                    return NUMBER;
                } else if (c == '+' || c == '-') {
                    return OP;
                } else if (c == '.') {
                    return POINT;
                } else if (c =='e' || c == 'E') {
                    return E;
                } else {
                    return null;
                }
            }
        }
        public enum State {
            INIT(false),
            OP1(false),
            // 在.前面的数字
            BEFORE_POINT_NUMBER(true),
            // 前面没数字的点
            NO_BEFORE_NUMBER_POINT(false),
            // 前面有数字的点
            BEFORE_NUMBER_POINT(true),
            // 点后面的数字
            AFTER_POINT_NUMBER(true),
            // e/E
            OPE(false),
            // E后面的符号
            OP2(false),
            // e后面的数字
            AFTER_E_NUMBER(true);
 
            // 是否可在这个状态结束
            private boolean canEnd;
 
            State(boolean canEnd) {
                this.canEnd = canEnd;
            }
 
            public boolean isCanEnd() {
                return canEnd;
            }
        }
 
        public Map<State, Map<CharType, State>> transferMap = new HashMap<>() {{
            Map<CharType, State> map = new HashMap<>() {{
                put(CharType.OP, State.OP1);
                put(CharType.NUMBER, State.BEFORE_POINT_NUMBER);
                put(CharType.POINT, State.NO_BEFORE_NUMBER_POINT);
            }};
            put(State.INIT, map);
 
            map = new HashMap<>() {{
                put(CharType.POINT, State.NO_BEFORE_NUMBER_POINT);
                put(CharType.NUMBER, State.BEFORE_POINT_NUMBER);
            }};
            put(State.OP1, map);
 
            map = new HashMap<>() {{
                put(CharType.POINT, State.BEFORE_NUMBER_POINT);
                put(CharType.NUMBER, State.BEFORE_POINT_NUMBER);
                put(CharType.E, State.OPE);
            }};
            put(State.BEFORE_POINT_NUMBER, map);
 
            map = new HashMap<>() {{
                put(CharType.NUMBER, State.AFTER_POINT_NUMBER);
            }};
            put(State.NO_BEFORE_NUMBER_POINT, map);
 
            map = new HashMap<>() {{
                put(CharType.NUMBER, State.AFTER_POINT_NUMBER);
                put(CharType.E, State.OPE);
            }};
            put(State.BEFORE_NUMBER_POINT, map);
 
            map = new HashMap<>() {{
                put(CharType.E, State.OPE);
                put(CharType.NUMBER, State.AFTER_POINT_NUMBER);
            }};
            put(State.AFTER_POINT_NUMBER, map);
            map = new HashMap<>() {{
                put(CharType.OP, State.OP2);
                put(CharType.NUMBER, State.AFTER_E_NUMBER);
            }};
            put(State.OPE, map);
            map = new HashMap<>() {{
                put(CharType.NUMBER, State.AFTER_E_NUMBER);
            }};
            put(State.OP2, map);
 
            map = new HashMap<>() {{
                put(CharType.NUMBER, State.AFTER_E_NUMBER);
            }};
            put(State.AFTER_E_NUMBER, map);
        }};
        public boolean isNumber(String s) {
            State state = State.INIT;
            for (char c : s.toCharArray()) {
                Map<CharType, State> transMap = transferMap.get(state);
                CharType charType = CharType.toCharType(c);
                if (charType == null) {
                    return false;
                }
                if (!transMap.containsKey(charType)) {
                    return false;
                }
                // 状态变更
                state = transMap.get(charType);
            }
            return state.canEnd;
        }
    }

从下面的代码可以看到，未来只需要维护transferMap 即可，非常方便，代码的优秀设计模式是一门造福懒人程序员们的艺术，重构出一个易于维护的代码也是程序员的成就感来源之一。

并发编程的艺术：诡异的Java代码揭示了cpu缓存的原理

著名的Java并发编程大师Doug lea在JDK 7的并发包里新增一个队列集合类Linked-TransferQueue，它在使用volatile变量时，用一种追加字节的方式来优化队列出队和入队的性能。LinkedTransferQueue的代码如下,着重关注p0~pe的定义：

/** 队列中的头部节点 */
private transient final PaddedAtomicReference<QNode> head;
/** 队列中的尾部节点 */
private transient final PaddedAtomicReference<QNode> tail;
static final class PaddedAtomicReference <T> extends AtomicReference T> {
     // 使用很多4个字节的引用追加到64个字节
     Object p0, p1, p2, p3, p4, p5, p6, p7, p8, p9, pa, pb, pc, pd, pe;
     PaddedAtomicReference(T r) {
        super(r);
     }
}
public class AtomicReference <V> implements java.io.Serializable {
     private volatile V value;
     // 省略其他代码
｝

追加字节能优化性能？这种方式看起来很神奇，但如果深入理解处理器架构就能理解其中的奥秘：（以下的解释来自《Java并发编程的艺术一书》 ）

“因为对于英特尔酷睿i7、酷睿、Atom和NetBurst，以及Core Solo和Pentium M处理器的L1、L2或L3缓存的高速缓存行是64个字节宽，不支持部分填充缓存行。

这意味着，如果队列的头节点和尾节点都不足64字节的话，处理器会将它们都读到同一个高速缓存行中，在多处理器下每个处理器都会缓存同样的头、尾节点。

当一个处理器试图修改头节点时，会将整个缓存行锁定，那么在缓存一致性机制的作用下，会导致其他处理器不能访问自己高速缓存中的尾节点，而队列的入队和出队操作则需要不停修改头节点和尾节点，所以在多处理器的情况下将会严重影响到队列的入队和出队效率。

因此Doug lea使用追加到64字节的方式来填满高速缓冲区的缓存行，避免头节点和尾节点加载到同一个缓存行，使头、尾节点在修改时不会互相锁定。

可以看到，在java的并发代码中能够体现底层缓存的设计。虽然这代码不太符合java希望屏蔽底层实现细节的设计理念，但是Doug lea大师对细节的考虑仍然让人赞叹不已。

算法的艺术：用搜索解决迷宫问题

学习数据结构时，相信“深度优先搜索”和“广度优先搜索”对初学者来说一度是一个噩梦，做练习题时也是用各种姿势遍历去二叉树，无法感受到乐趣所在。

但是当你用搜索来解决比较简单的迷宫寻路问题时，便会感到算法的魅力。

想起小时候玩一些RPG游戏，往往会有各种迷宫，每次自己探索出口时，其实就是用的深度搜索，找不到会回溯，然而这样费时间也费脑子，当地图过大，大脑的缓存不足，或者思考深度不足时，解决起来就很困难。

但如果有计算机的帮忙，对于每次的移动，给定地图输入，使用搜索算法、A*等算法，便能够快速找到迷宫的离开路线。

下面给出一个伪代码，来简单解释搜索问题是怎么解决问题的：

搜索（当前地图，当前点） {
  If (是否已经搜索过这个场景) {
    Return;
    }

  If(是否到达边界) {
      刷新最新结果;
      return;
  }

  for(遍历当前点的所有选择) {
      if (是否是无效的选择) {
          continue;
          }
 
      将当前选择带来的变化更新到地图中
      进入后续的搜索
      回退当前选择带来的变化
   }
}

所以当你学习完搜索算法，却还对其应用感到困惑时，不妨来做一道迷宫寻路题.（例如http://poj.org/problem?id=3984）

或者自己写一个五子棋对战程序与自己对战。对战程序除了搜索算法，还要考虑博弈论的思想，通过alpha-beta算法来处理敌对双方对结果的选择，编写评估函数来定义对局面好坏的判断， 整个编写过程会更加复杂而有趣,不妨作为自己对搜索算法更深层次的学习时尝试一番。

二进制的艺术：用数学节省了空间

“给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素，而且不能用额外空间”

甚至还有升级版：

“给你一个整数数组 ，除某个元素仅出现一次外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。”

第一想法肯定是维护一个哈希表或者数组。但是问题要求不能用额外空间，这一般都是为了在有成本限制的环境下考虑和设计的，例如内存有限的某些硬件设备中。

因此在最佳解法中，选择借助了二进制来解决这个问题。通过同位异或得0，不同位异或得1的特性，快速过滤掉相同的数字：

class Solution {
    public int singleNumber(int[] nums) {
        int result = 0;
        for(int num : nums) {
            result ^= num;
        }
        return result;
    }
}

是不是感觉非常巧妙有趣，利用数学的二进制特性，简单的异或就搞定了本来需要大量内存的问题，不禁令人拍案叫绝。

本文参与华为云社区【内容共创】活动第16期。

点击关注，第一时间了解华为云新鲜技术~