有向图的强连通分量与无向图的双连通分量总结

首先我们需要搞懂图论中的一些基础概念

完全图: 假设一个图有

     n
    
   
   
    n
   
  
 n 个顶点, 并且每两个点之间都有边就叫完全图

连通图(多指无向图): 对于两个点,

     u
    
    
     ,
    
    
     v
    
    
     ,
    
   
   
    u,v,
   
  
 u,v, 如果
 
  
   
    
     u
    
    
     ,
    
    
     v
    
   
   
    u,v
   
  
 u,v 之间有通路,则称 
 
  
   
    
     u
    
    
     ,
    
    
     v
    
   
   
    u,v
   
  
 u,v 两点连通, 如果图中任意两个点都连通, 则称这个图为连通图

连通分量: 连通分量中任意两点

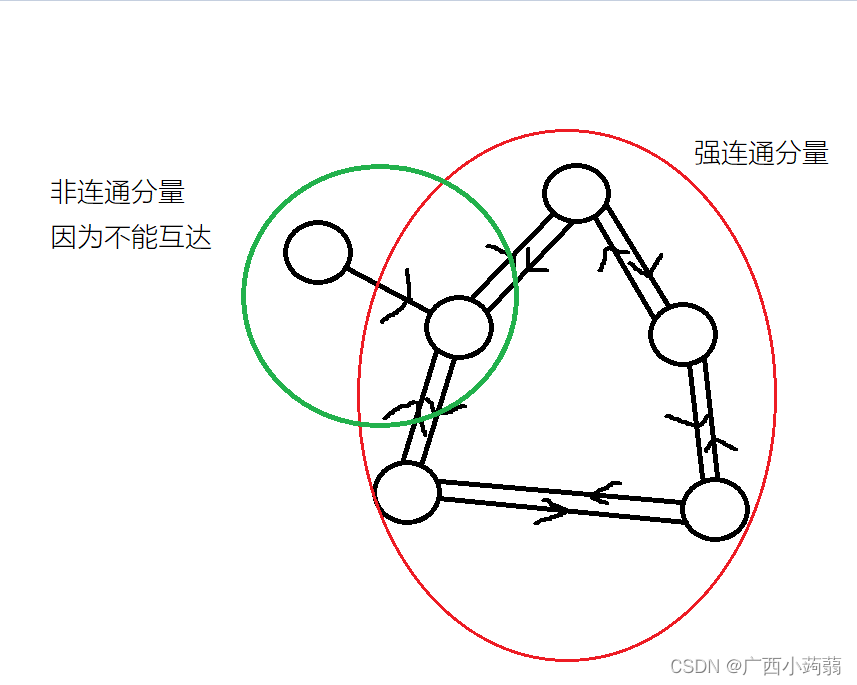
     u
    
    
     ,
    
    
     v
    
    
     ,
    
   
   
    u,v,
   
  
 u,v, 两两之间必定能互相到达, 
 
  
   
    
     u
    
    
     −
    
    
     >
    
    
     v
    
    
     ,
    
    
     v
    
    
     −
    
    
     >
    
    
     u
    
    
     .
    
   
   
    u->v, v->u.
   
  
 u−>v,v−>u. (当然一个点也是连通分量)

强连通分量: 极大的连通分量,对于连通分量内部的任意两个点

     u
    
    
     ,
    
    
     v
    
    
     ,
    
   
   
    u, v,
   
  
 u,v,, 既存在 
 
  
   
    
     u
    
   
   
    u
   
  
 u 到 
 
  
   
    
     v
    
   
   
    v
   
  
 v 的路径, 又存在 
 
  
   
    
     v
    
   
   
    v
   
  
 v 到 
 
  
   
    
     u
    
   
   
    u
   
  
 u的路径,并且如果再加入其它点和边就不再连通的,

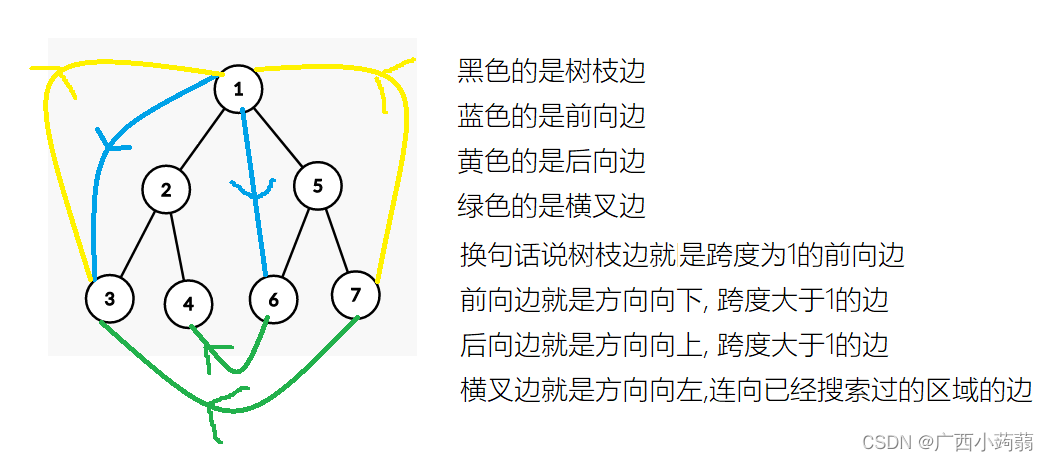
tarjan算法求强连通分量

了解

    t
   
   
    a
   
   
    r
   
   
    j
   
   
    a
   
   
    n
   
  
  
   tarjan
  
 
tarjan 算法之前你必须了解一个概念, 时间戳

时间戳: 根据深度优先搜索的顺序给节点标号
有了时间戳后我们就可以引入两个概念:

    d
   
   
    f
   
   
    n
   
   
    [
   
   
    u
   
   
    ]
   
  
  
   dfn[u]
  
 
dfn[u]: 节点 

 
  
   
    u
   
  
  
   u
  
 
u 所对应的时间戳


 
  
   
    l
   
   
    o
   
   
    w
   
   
    [
   
   
    u
   
   
    ]
   
  
  
   low[u]
  
 
low[u]: 节点 

 
  
   
    u
   
  
  
   u
  
 
u 所能够到达的时间戳的最小值

如果

    d
   
   
    f
   
   
    n
   
   
    [
   
   
    u
   
   
    ]
   
   
    =
   
   
    =
   
   
    l
   
   
    o
   
   
    w
   
   
    [
   
   
    u
   
   
    ]
   
  
  
   dfn[u] == low[u]
  
 
dfn[u]==low[u]

 
  
     
   
    ⟺
     
  
  
   \iff
  
 
⟺

 
  
   
    u
   
  
  
   u
  
 
u 节点是所在强连通分量的最高点

判断一个点是否在某个强连通分量中

     
   
    ⟺
     
  
  
   \iff
  
 
⟺ 该点是否能走到该强连通分量的最高点

tarjan 算法求强连通分量的步骤

1. 缩点
2. 建图
3. 求拓扑序(递推)

1.缩点

voidtarjan(int u){
    dfn[u]= low[u]=++ timestamp;//分配编号
    
    s.push(u), is_stack[u]=true;//入栈, 标记为在栈中for(int i = h[u];~i; i = ne[i])//遍历每条邻边{int j = e[i];if(!dfn[j])//如果这个点没有被搜索过{tarjan(j);//搜到底
            low[u]= std ::min(low[u], low[j]);//用j更新u}elseif(is_stack[j])  low[u]= std ::min(low[u], dfn[j]);//如果这个点没被搜到过, 并且在栈中, 说明存在横叉边}if(dfn[u]== low[u])//u点是所在强连通分量的最高点{int y;
        scc_cnt ++;//强联通分量数量++do{
            y = s.top();//取出栈顶
            s.pop();
            size[scc_cnt]++;//该连通分量中点的数量++
            id[y]= scc_cnt;//分配编号
            is_stack[y]=false;//标记为不在栈中}while(y != u);}}

2.建图

for(int i =1; i <= n; i ++)for(int j = h[i];~j; j = ne[j]){int k = e[j];int a = id[i], b = id[k];if(a != b)add(hs,a, b);//hs为新图的头结点}

3.求拓扑序

for(int i = scc_cnt; i; i --)

因为

    t
   
   
    a
   
   
    r
   
   
    j
   
   
    a
   
   
    n
   
  
  
   tarjan
  
 
tarjan 算法最后求出来的就是逆拓扑序, 所以不用再进行拓扑排序了

无向图的双连通分量
1.边的双连通分量

    e
   
   
    −
   
   
    d
   
   
    c
   
   
    c
   
  
  
   e-dcc
  
 
e−dcc 极大的不包含桥的连通块

2.点的双连通分量

    v
   
   
    −
   
   
    d
   
   
    c
   
   
    c
   
  
  
   v-dcc
  
 
v−dcc 极大的不包含割点的连通块

首先要知道桥是什么?
桥 就是去掉这条边后, 能使连通块数量增加的边(或者说使得这个图不连通)
割点 就是去掉这个点和它所关联的边,能使得连通块数量增加的点(或者说使得这个图不连通)

点双连通分量的特殊性质
除了只包含两个点的点双连通分量外, 其他点双连通分量都满足一个性质:

     任
    
    
     意
    
    
     两
    
    
     点
    
    
     间
    
    
     都
    
    
     存
    
    
     在
    
    
     不
    
    
     相
    
    
     交
    
    
     的
    
    
     两
    
    
     条
    
    
     路
    
    
     径
    
   
   
    任意两点间都存在不相交的两条路径
   
  
 任意两点间都存在不相交的两条路径

任何一个割点都存在于两个点双连通分量中
因为删去割点后, 图就不连通了, 所以割点连接的一定是不相同的两个点双连通分量

任意一个非割点都只存在于一个点双连通分量中

节点

    1
   
   
    ,
   
   
    6
   
  
  
   1,6
  
 
1,6 是割点, 右边深色的是四个边双连通分量,可以看出每个割点都位于两个边双连通分量中


 
  
   
    t
   
   
    a
   
   
    r
   
   
    j
   
   
    a
   
   
    n
   
  
  
   tarjan
  
 
tarjan 求割点

割点的定义是删去这个点后图不连通, 那么肯定存在一些点,在不经过割点的情况下, 无法到达割点的祖先,所以我们可以通过这个性质去寻找割点

有割点

     
   
    ⟺
     
  
  
   \iff
  
 
⟺

 
  
   
    l
   
   
    o
   
   
    w
   
   
    [
   
   
    y
   
   
    ]
   
   
    ≥
   
   
    d
   
   
    f
   
   
    n
   
   
    [
   
   
    x
   
   
    ]
   
  
  
   low[y] ≥ dfn[x]
  
 
low[y]≥dfn[x]

这是什么意思呢? 就是说节点

    y
   
  
  
   y
  
 
y 能够到达的最高点的时间戳比 

 
  
   
    x
   
  
  
   x
  
 
x 的时间戳要大, 说明 节点

 
  
   
    y
   
  
  
   y
  
 
y无法到达 节点

 
  
   
    x
   
  
  
   x
  
 
x 的祖先, 所以如果删除节点 

 
  
   
    x
   
  
  
   x
  
 
x, 就不连通了

这里存在两种情况:

1. 如果 x x x 不是根节点, 那么只要 l o w [ y ] ≥ d f n [ x ] low[y] ≥ dfn[x] low[y]≥dfn[x] , x 必然是割点
2. 如果 x x x 是根节点, 如果只有一个子节点, 删去 x x x及与 x x x 相关联的边后, 图还是连通的, 不满足割点定义, 所以如果 x x x 是根节点, 还需要 x x x 有两个子节点

为了求出"点双连通分量", 需要在

    t
   
   
    a
   
   
    r
   
   
    j
   
   
    a
   
   
    n
   
  
  
   tarjan
  
 
tarjan 算法的过程中维护一个栈, 并按照如下方法维护栈中的元素:

1. 当一个节点第一次访问时,把该节点入栈
2. 当割点判定法则中的条件 l o w [ y ] ≥ d f n [ x ] low[y] ≥ dfn[x] low[y]≥dfn[x] 成立时, 无论 x x x 是否为根, 都要: (1):从栈顶不断弹出节点, 直至节点 y y y 被弹出 (2): 刚才弹出的所有节点与节点 x x x 一起构成一个 v − D C C v-DCC v−DCC(点双连通分量); 模板:

voidtarjan(int u){
     dfn[u]= low[u]=++ timestamp;// 分配时间戳
     stk[++ tt]= u;//入栈if(u == root && h[u]!=-1){
         dcc_cnt ++;
         dcc[dcc_cnt].push_back(u);return;}int cnt =0;//记录节点u下, 子树的数量for(int i = h[u];~i; i = ne[i]){int j = e[i];if(!dfn[j]){tarjan(j);
             low[u]=min(low[u], low[j]);if(low[y]>= dfn[x]){
                 cnt ++;if(u != root || cnt >1) cut[u]=true;//如果是子树大于1, 或者是根节点,那么这个点就是割点
                 dcc_cnt ++;int y;do{
                     y = stk[tt --];
                     dcc[dcc_cnt].push_back(y);}while(y != j);//到j就退出了, 此时u还未被弹出//u作为割点既可以和这个组成v-dcc也可以和另一个组成v-dcc
                 dcc[dcc_cnt].push_back(u);}else low[u]=min(low[u], dfn[j]);}}}

边的双连通分量

要求边的双连通分量首先需要找到 桥,

    x
   
  
  
   x
  
 
x 与 

 
  
   
    y
   
  
  
   y
  
 
y 之间是桥 

 
  
     
   
    ⟺
     
  
  
   \iff
  
 
⟺

 
  
   
    l
   
   
    o
   
   
    w
   
   
    [
   
   
    y
   
   
    ]
   
   
    >
   
   
    d
   
   
    f
   
   
    n
   
   
    [
   
   
    x
   
   
    ]
   
  
  
   low[y] > dfn[x]
  
 
low[y]>dfn[x]

你会发现这和割点判断的很相似, 我们不妨来梳理一下

    l
   
   
    o
   
   
    w
   
   
    [
   
   
    u
   
   
    ]
   
   
    =
   
   
    =
   
   
    d
   
   
    f
   
   
    n
   
   
    [
   
   
    u
   
   
    ]
   
  
  
   low[u] == dfn[u]
  
 
low[u]==dfn[u]

 
  
     
   
    ⟺
     
  
  
   \iff
  
 
⟺

 
  
   
    u
   
  
  
   u
  
 
u点是强连通分量的最高点


 
  
   
    l
   
   
    o
   
   
    w
   
   
    [
   
   
    y
   
   
    ]
   
   
    ≥
   
   
    d
   
   
    f
   
   
    n
   
   
    [
   
   
    x
   
   
    ]
   
  
  
   low[y] ≥ dfn[x]
  
 
low[y]≥dfn[x]

 
  
     
   
    ⟺
     
  
  
   \iff
  
 
⟺

 
  
   
    x
   
  
  
   x
  
 
x是割点


 
  
   
    l
   
   
    o
   
   
    w
   
   
    [
   
   
    y
   
   
    ]
   
   
    >
   
   
    d
   
   
    f
   
   
    n
   
   
    [
   
   
    x
   
   
    ]
   
  
  
   low[y] > dfn[x]
  
 
low[y]>dfn[x]

 
  
     
   
    ⟺
     
  
  
   \iff
  
 
⟺

 
  
   
    x
   
  
  
   x
  
 
x 和 

 
  
   
    y
   
  
  
   y
  
 
y 之间有桥

如何找到所有的边的双连通分量 ?
因为边的双连通分量是不包含桥的极大连通分量, 所以我们必须将所有的桥删掉

voidtarjan(int u,int fa){
    dfn[u]= low[u]=++ timestamp;//分配时间戳

    stk[++ tt]= u;//入栈for(int i = h[u];~i; i = ne[i])//遍历每条邻边{int j = e[i];if(!dfn[j]){tarjan(j, i);//搜到底
            low[u]=min(low[j], low[u]);//用j更新uif(low[j]> dfn[u])//判定为桥
                is_bridge[i]= is_bridge[i ^1]=true;}//如果走到了j, 并且j不是由fa的反向边走过来的 elseif(i !=(fa ^1)) low[u]=min(low[u], dfn[j]);}if(dfn[u]== low[u])//走到了该连通分量的最高点{int y;++dcc_cnt;do{
            y = stk[tt --];//取出
            id[y]= dcc_cnt;//分配编号}while(y != u);}}

完结✿✿ヽ(°▽°)ノ✿! 给个赞吧!