图像处理入门
C语言生成RGB24格式图像
图像缩放之最近邻内插法
图像直方图均衡化数学原理和程序实现
一、图像均衡化数学原理
1.转化为数学问题
已知随机变量X的分布函数*F**x**(**𝑥**)*和概率密度fx (x),以及对随机变量进行Y=g(X)变化后的随机变量的概率密度1/(L-1),g(x)为单调连续,求转换函数y=g(x)。
2.需要用到的知识
一维函数微积分
随机变量的概率分布
3.数学推理

二、程序实现
1.程序实现原理

2.代码实现
代码如下(示例):
#include <stdlib.h>
#include <stdio.h>
#define PICT_WIDTH 90
#define PICT_HEIGHT 60
static unsigned int s_rgb[PICT_WIDTH][PICT_HEIGHT][3] = { 0 };
/**
* rgb24
* r:203 g:64,173,38 b:142
*/
int make_rgb24_colorbar(unsigned int rgb[90][60][3])
{
int i = 0;
int j = 0;
unsigned char chr = 0;
for (j = 0; j<PICT_HEIGHT; j++)
{
for (i = 0; i < PICT_WIDTH; i++)
{
if (i<30)
{
chr = 203;
}
else if (i<60)
{
chr = 64;
}
else
{
chr = 0;
}
rgb[i][j][0] = chr;
if (i<30)
{
chr = 0;
}
else if (i<60)
{
chr = 173;
}
else
{
chr = 0;
}
rgb[i][j][1] = chr;
if (i<30)
{
chr = 0;
}
else if (i<60)
{
chr = 38;
}
else
{
chr = 142;
}
rgb[i][j][2] = chr;
}
}
return 0;
}
int generate_rgb24_file(unsigned int rgb[90][60][3],char *file_name)
{
char file_path[64] = {0};
if (file_name == NULL)
{
return 0;
}
snprintf(file_path,63,"rgb_%s_90_60.rgb24", file_name);
FILE *fp = fopen(file_path, "wb+");
int i = 0;
int j = 0;
unsigned char chr = 0;
for (j = 0; j< PICT_HEIGHT; j++)
{
for (i = 0; i < PICT_WIDTH; i++)
{
chr = rgb[i][j][0];
fwrite(&chr, 1, 1, fp);
chr = rgb[i][j][1];
fwrite(&chr, 1, 1, fp);
chr = rgb[i][j][2];
fwrite(&chr, 1, 1, fp);
}
}
fclose(fp);
return 0;
}
#define IMAGE_COLOR_LEVEL 256
#define HISTOGRAM_HEIGHT_MAX 20
#define HISTOGRAM_WIDTH_MAX 128
#define STATISTIC_DEC_MAX 5
#define STATISTIC_HOR_AXS_NUM (HISTOGRAM_WIDTH_MAX / STATISTIC_DEC_MAX)
int print_histogram(int image_statistic[IMAGE_COLOR_LEVEL])
{
int *image_point = image_statistic;
char hist_char = '*';
char hist_space_char = ' ';
char disp_array[HISTOGRAM_HEIGHT_MAX][HISTOGRAM_WIDTH_MAX + 1] = {0};
int hist_statistic[HISTOGRAM_WIDTH_MAX] = {0};
int i = 0;
int j = 0;
int k = 0;
int statistic_max = 0;
int hist_hor_axis[STATISTIC_HOR_AXS_NUM] = { 0 };
for (i = 0; i < IMAGE_COLOR_LEVEL; i++)
{
hist_statistic[i * HISTOGRAM_WIDTH_MAX / IMAGE_COLOR_LEVEL] += image_statistic[i];
}
for (i = 0; i < STATISTIC_HOR_AXS_NUM; i++)
{
hist_hor_axis[i] = 1.0 * STATISTIC_DEC_MAX * i * IMAGE_COLOR_LEVEL / HISTOGRAM_WIDTH_MAX;
}
for (i = 0; i < HISTOGRAM_WIDTH_MAX; i++)
{
if (hist_statistic[i] > statistic_max)
{
statistic_max = hist_statistic[i];
}
}
for (i = 0; i < HISTOGRAM_WIDTH_MAX;i++)
{
int hist_height = hist_statistic[i] * HISTOGRAM_HEIGHT_MAX / statistic_max;
for (j = 0; j < HISTOGRAM_HEIGHT_MAX; j++)
{
if (j < hist_height)
{
disp_array[j][i] = hist_char;
}
else
{
disp_array[j][i] = hist_space_char;
}
}
}
printf(
" y\n"
" \n"
" |\n"
"%5d|\n", statistic_max);
for (i = 0; i < HISTOGRAM_HEIGHT_MAX; i++)
{
printf(
" |%s\n", disp_array[HISTOGRAM_HEIGHT_MAX - i - 1]);
}
printf(
" |--------------------------------------------------------------------------------------------------------------------------------->x\n");
printf(
" ");
char dec_max[32] = { 0 };
char format_str[32] = "%-";
sprintf(dec_max, "%d", STATISTIC_DEC_MAX);
strncat(format_str, dec_max,32);
strncat(format_str, "d", 32);
for (i = 0; i < STATISTIC_HOR_AXS_NUM; i++)
{
printf(
format_str, hist_hor_axis[i]);
}
printf(
"\n");
return 0;
}
int statistic_histogram(unsigned int rgb[90][60][3],int image_statistic[IMAGE_COLOR_LEVEL])
{
int i = 0;
int j = 0;
int k = 0;
for(i = 0; i < 90; i++)
{
for (j = 0; j < 60; j++)
{
for (k = 0; k < 3; k++)
{
image_statistic[rgb[i][j][k]]++;
}
}
}
return 0;
}
//直方图均衡化
int histogram_equalization(unsigned int rgb[90][60][3], unsigned int result_rgb[90][60][3])
{
int image_statistic[IMAGE_COLOR_LEVEL] = {0};
int image_statistic2[IMAGE_COLOR_LEVEL] = {0};
int i = 0;
int j = 0;
int k = 0;
int tmp = 0;
int pixel_num = 90 * 60 * 3;
float ratio = 0;
float equal_ratio[IMAGE_COLOR_LEVEL] = { 0 };
statistic_histogram(rgb, image_statistic);
for (i = 0; i < IMAGE_COLOR_LEVEL; i++)
{
if(image_statistic[i] != 0)
{
printf("before,i:[%d],num:[%d]\n",i,image_statistic[i]);
}
}
for (i = 0; i < IMAGE_COLOR_LEVEL; i++)
{
for (j = 0; j < i + 1; j++)
{
equal_ratio[i] += image_statistic[j] * 1.0 / pixel_num;
}
}
for (i = 0; i < 90; i++)
{
for (j = 0; j < 60; j++)
{
for (k = 0; k < 3; k++)
{
result_rgb[i][j][k] = (unsigned int)(IMAGE_COLOR_LEVEL - 1) * equal_ratio[rgb[i][j][k]];
}
}
}
statistic_histogram(result_rgb, image_statistic2);
for (i = 0; i < IMAGE_COLOR_LEVEL; i++)
{
if(image_statistic2[i] != 0)
{
printf("after,i:[%d],num:[%d]\n",i,image_statistic2[i]);
}
}
return 0;
}
int main()
{
int image_statistic[IMAGE_COLOR_LEVEL] = {0};
make_rgb24_colorbar(s_rgb);
generate_rgb24_file(s_rgb, "colorbar");
statistic_histogram(s_rgb, image_statistic);
print_histogram(image_statistic);
unsigned int result_rgb[90][60][3];
int result_statistic[IMAGE_COLOR_LEVEL] = { 0 };
histogram_equalization(s_rgb, result_rgb);
statistic_histogram(result_rgb, result_statistic);
print_histogram(result_statistic);
generate_rgb24_file(result_rgb,"equalization");
sleep(100);;
return 0;
}
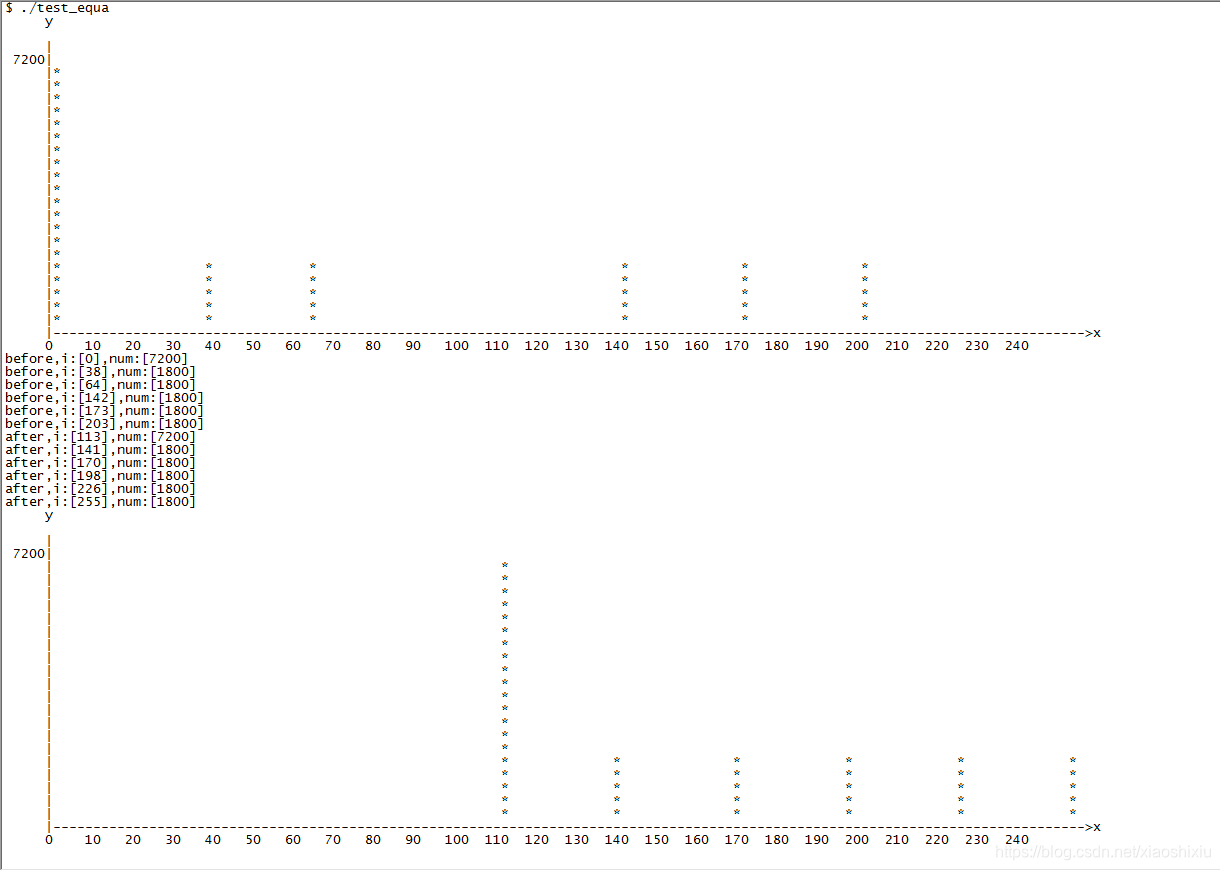
3.程序执行效果
4.图像均衡化前后效果
均衡化前:

均衡化后:

总结
均衡化后直方图更均匀,但是实际图像质量不一定更好。
标签:
直方图均衡 化
本文转载自: https://blog.csdn.net/xiaoshixiu/article/details/118559610
版权归原作者 上天肖 所有, 如有侵权,请联系我们删除。
版权归原作者 上天肖 所有, 如有侵权,请联系我们删除。