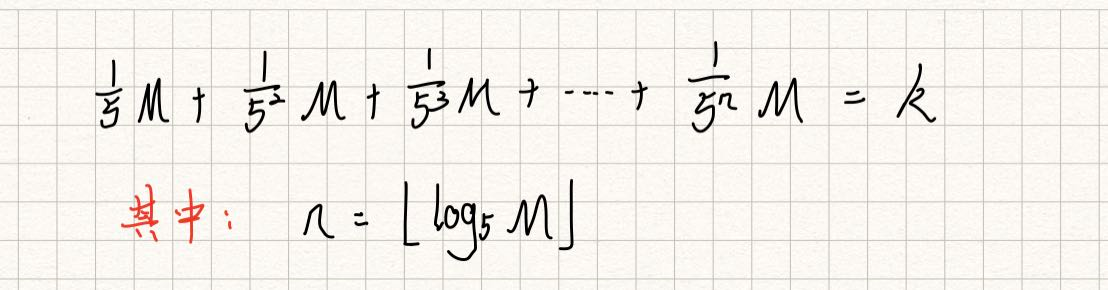🚀写在前面
Hello大家好😋，我是秋刀鱼🐟，一只活跃于Java区与算法区的新人博主~
欢迎大家加入高校算法学习社区： https://bbs.csdn.net/forums/Suanfa，社区里大佬云集，大家互相交流学习！
蓝桥杯比赛终于告一段落了，感谢这一路上付出的你🧡。这道求阶乘题目是今天较难的一道题目，这里我给大家分享下我的解题思路，不代表一定正确！仅供参考😋。
** 🎉🎉期待你的支持与关注🎉🎉**
🎉🎉主页：秋刀鱼与猫🎉🎉
🛸目录
🚀题目描述
🚀解题思路（仅供参考）
**题目给定K的最大值为
1 0 18 10^{18} 1018，显然暴力解法是无法AC的，此时就需要更换思路。**题目中所求的是一个数阶乘后0的数量，不妨想想什么样的情况下会产生0呢？只有乘法运算为：2*5 时才会产生一位的 0 ，其余乘法运算均不会产生0。
**有了这个结论，不妨我们假设返回的结果为
M M M ，也就是说 M ! M! M! 后存在 k k k 个0。为了找到式中有多少个 2*5，不妨我们将每一个数进行拆分为其因子，因为 2 因子出现的次数远大于 5 因子出现的次数，因此只需要找到 [ 1 , M ] [1,M] [1,M] 区间内的数中 5 因子的个数就是 k k k 的值。如果直接遍历 5 的倍数5,10,15,20,...,进行寻找必定会超时，因为数据量实在是太大了，因此下面进行第二次探究。**
**这样思考：
5能够提供 1 个5因子，
25能够提供 2 个5因子，
125能提供 3 个5因子，…，那么现在给定一个值
M M M ，如何计算其 5因子的总数呢？先看看下面这张图：**
对于所有能整除5的数来说：如果其存在5因子，则第一列的值存在；如果其存在25因子，则第二列的值存在；如果其存在125因子，则第三列的值存在，这样顺序推导下去：
**那么对于
[ 1 , M ] [1,M] [1,M]区间内的所有值：值存在5因子的数量为： M / 5 M/5 M/5 ；值存在25因子的数量为： M / 25 M/25 M/25 ；值存在125的数量为： M / 125 M/125 M/125…，所有这些值的和，就是 5 因子的总数 K K K****因此推导出5因子总数K与结果值
M M M的关系为：**
**通过等比数列求和公式化简为：
( 1 − ( 1 / 5 ) n ) M = 4 K (1-(1/5)^n)M=4K (1−(1/5)n)M=4K，所以当 n − > + I N F n->+INF n−>+INF 时， M = 4 k M=4k M=4k。又因为 K K K的最大值为： 1 0 18 10^{18} 1018，因此 M M M的最大值为 4 ∗ 1 0 18 4*10^{18} 4∗1018，所以 n n n的最大值也可以计算出来，这里假定为 30 30 30。****现在输入一个数据
K K K后，根据公式 ( 1 − ( 1 / 5 ) n ) M = 4 K (1-(1/5)^n)M=4K (1−(1/5)n)M=4K ，计算出不同的 n n n值对应的 4 K / ( 1 − ( 1 / 5 ) n ) 4K/(1-(1/5)^n) 4K/(1−(1/5)n)的值放入数组 n u m s nums nums中，在以 n n n从小到大的顺序（保证 M M M值最小）判断 n u m s [ n ] nums[n] nums[n]的值是否符合要求（即： 5 n 5^n 5n是最大的小于等于 n u m s [ n ] nums[n] nums[n]的5的幂）。****如果判断是符合要求的数，因为
M M M的值要求：最小、 M > = n u m s [ n ] M>=nums[n] M>=nums[n]、 M % 5 = = 0 M \%5 ==0 M%5==0恒成立，因此计算出来的 n u m s [ n ] nums[n] nums[n]需要特殊处理，也就是找到第一个大于等于 n u m s [ n ] nums[n] nums[n]且取余5为0的值，就是 M M M。****最后将
M,K,n的值代入原式中判断等式是否成立，如果成立则等式输出
M，否则输出
-1。**
🚀代码（仅供参考）
因为蓝桥杯系统该题的调试还没有上线，因此该代码仅供参考！
import java.util.Scanner;publicclassMain{staticbooleanjudge(long k,long M,int n){long m =5;while(n >=1){
k -=(M / m);--n;
m *=5;}return k ==0;}staticdouble[] nums =newdouble[30];publicstaticvoidmain(String[] args){
Scanner cin =newScanner(System.in);long k = cin.nextLong();for(int i =1; i <30;++i){
nums[i]=(4* k)/(1- Math.pow(0.2, i *1.0));}for(int i =1; i <30;++i){double cur = Math.pow(5, i);double tCur = Math.pow(5, i +1);if(nums[i]>= cur && nums[i]*1.0< tCur){long lI =(long)(nums[i]);int mod =(int)(lI %5);if(lI != nums[i]){
lI +=5;}
lI -= mod;if(judge(k, lI, i)){
System.out.println(lI);return;}}}
System.out.println(-1);}}
🧡写在最后
比赛虽然告一段落，但未来的路还有很长，我们应当砥砺前行、共同进步，为美好的明天而战🤗！
本文转载自: https://blog.csdn.net/qq_51439643/article/details/124062427
版权归原作者 秋刀鱼与猫_ 所有， 如有侵权，请联系我们删除。
版权归原作者 秋刀鱼与猫_ 所有， 如有侵权，请联系我们删除。