利用QT 的 Graphics View 系统实现一个简易的 Graph Editor

QT 中的 Graphics View 系统. 是一个相对成熟的渲染引擎的上层框架，通常也可以会叫做 Scene - View。

通常会有 QGraphicsView, QGraphicsScene, QGraphicsItem 这几个类构成。

view是视口(viewport)；scene是一个场景，负责容纳各种item；而item就是可见的这些元件。

一般来说，绘图可以使用 QPainter直接在重绘事件中进行绘制，但是，当我们想要选择绘制的图形的时候，就犯难了。我们的painter是直接在屏幕上写写画画，没有人来管理，在当前的mouse事件中也不知道如何处理这些项。

这个时候，Graphics View 就解决了这个问题，通过scene来管理各种图元item项。item在scene上绘制，scene在view上显示。

本文，就是利用Graphics View 系统来实现了一个简单的有向图/无向图编辑器。

编辑的图输出效果如下：

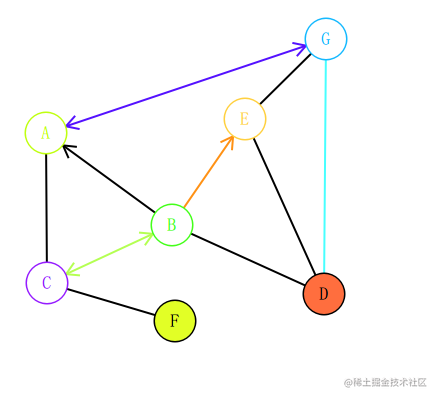
绘制点和绘制线是一个图元，那么就是一个 QGraphicsItem，继承自 QGraphicsItem，然后去重写绘制方法

在绘制点和线的时候，需要重写QGraphicsItem的绘制函数，也就是

paint(QPainter *painter, const QStyleOptionGraphicsItem *option, QWidget *widget)

如何绘制点

graphNode

类的设计：

classgraphNode:publicQObject,publicQGraphicsItem{
    Q_OBJECT
public:graphNode(QPointF point,int r =10, QString str ="0");// QGraphicsItem interfacepublic:
    QRectF boundingRect()constoverride;voidpaint(QPainter *painter,const QStyleOptionGraphicsItem *option, QWidget *widget)override;

    QPointF getPoint()const;intgetR()const;voidsetR(int newR);const QString &getText()const;voidsetText(const QString &newText);const QColor &getFrontColor()const;voidsetFrontColor(const QColor &newFrontColor);const QColor &getBackColor()const;voidsetBackColor(const QColor &newBackColor);intgetRoundWidth()const;voidsetRoundWidth(int newRoundWidth);private:
    QPointF point;// 绘制的初始点int r;// 半径
    QString text;// 点的文字
    QColor frontColor;// 前景色Ⅰ
    QColor backColor;// 背景色Ⅰint roundWidth;// 圆的宽Ⅰ};

在这个类中，我自定义了一些属性，方便配置点的颜色，大小等等。

核心还是在于paint函数，其余都是辅助功能

下面是paint函数的实现：

void graphNode::paint(QPainter *painter,const QStyleOptionGraphicsItem *option, QWidget *widget){
    QPen pen;
    pen.setWidth(roundWidth);

    painter->setRenderHint(QPainter::HighQualityAntialiasing);if(option->state & QStyle::State_Selected)
        pen.setColor(QColor((frontColor.red()+125)%255,(frontColor.green())%255,(frontColor.blue()+125)%255));// 选中时颜色变化else pen.setColor(frontColor);

    painter->setPen(pen);
    painter->drawEllipse(QRectF(point.x()- r, point.y()- r, r *2, r *2));

    QPainterPath path;
    path.addEllipse(QRectF(point.x()- r, point.y()- r, r *2, r *2));
    painter->fillPath(path,QBrush(backColor));

    painter->drawText(boundingRect(),
                      Qt::AlignHCenter |
                      Qt::AlignVCenter, text);}

paint一共做了两件事情，第一件事情绘制一个圆，第二件事情就是绘制一个标识文字。

其中的A就是标识文字

如何绘制线

graphLine

类设计如下

classgraphLine:publicQObject,publicQGraphicsLineItem{
    Q_OBJECT

public:enumLineType{
        LeftToRight,// ==>
        RightToLeft,// <==
        TwoWayArrow,// <=>
        NoArrow,// <=>};explicitgraphLine(graphNode *begin,
                       graphNode *end,
                       LineType type = NoArrow,
                       QObject *parent =nullptr);private:
    graphNode *begin;
    graphNode *end;int length;
    QColor color;
    LineType lineType;private:voidpaintArrow(graphNode* begin, graphNode* end, QPainter* painter);public:
    QPainterPath shape()constoverride;voidpaint(QPainter *painter,const QStyleOptionGraphicsItem *option, QWidget *widget)override;const QColor &getColor()const;voidsetColor(const QColor &newColor);
    LineType getLineType()const;voidsetLineType(LineType newType);
    graphNode *getBegin()const;
    graphNode *getEnd()const;};

其中

paintArrow

用来绘制箭头

绘制线的线有两种，一种是不带箭头的，一种是带方向箭头的。

不带箭头

不带箭头的比较好绘制，计算一下起点和终点的坐标，画一条线就是。

auto r_begin = begin->getPoint()+ begin->pos();auto r_end = end->getPoint()+ end->pos();
    QLineF lines(r_begin, r_end);setLine(lines);

    QPen pen;
    pen.setWidth(2);

    painter->setPen(pen);
    painter->setRenderHint(QPainter::HighQualityAntialiasing);
    painter->drawLine(line());

带箭头

绘制箭头可能需要一些计算，不过由于我们这里这个图形选择的圆，其实还是比较容易计算的。

如果是多边形，要麻烦一点。

在这里，我们想要的效果是箭头始终紧贴着其指向的圆。

比如这种效果：

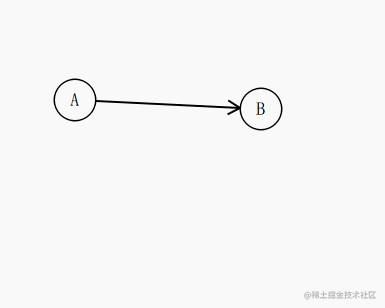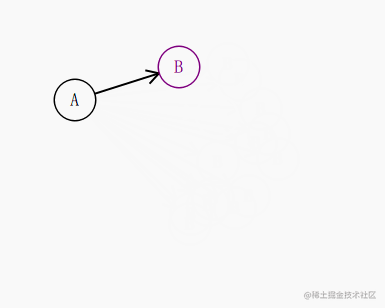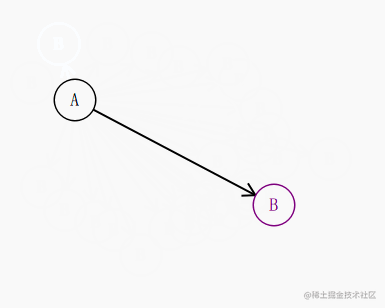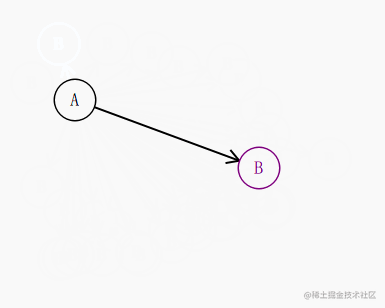
GIF 2023-1-13 16-54-33.gif

我们知道起点 a 和终点 b的坐标，知道圆的半径，其实就很容易的推导出圆和这条直线的交点是多少了。

大概是这样：

     点
    
    
     a
    
    
     坐标为
    
    
     (
    
    
     
      x
     
     
      1
     
    
    
     ,
    
    
     
      y
     
     
      1
     
    
    
     )
    
    
     ,
    
    
     点
    
    
     b
    
    
     坐标为
    
    
     (
    
    
     
      x
     
     
      2
     
    
    
     ,
    
    
     
      y
     
     
      2
     
    
    
     )
    
    
    
     现在，
    
    
     a
    
    
     b
    
    
     的距离
    
    
     =
    
    
     (
    
    
     
      x
     
     
      2
     
    
    
     −
    
    
     
      x
     
     
      1
     
    
    
     
      )
     
     
      2
     
    
    
     +
    
    
     (
    
    
     
      y
     
     
      2
     
    
    
     −
    
    
     
      y
     
     
      1
     
    
    
     
      )
     
     
      2
     
    
    
    
     直线
    
    
     a
    
    
     b
    
    
     的斜率为
    
    
     k
    
    
     =
    
    
     (
    
    
     
      y
     
     
      2
     
    
    
     −
    
    
     
      y
     
     
      1
     
    
    
     )
    
    
     /
    
    
     (
    
    
     
      x
     
     
      2
     
    
    
     −
    
    
     
      x
     
     
      1
     
    
    
     )
    
    
    
     现在点
    
    
     c
    
    
     (
    
    
     x
    
    
     ,
    
    
     y
    
    
     )
    
    
     在
    
    
     a
    
    
     b
    
    
     上，若与
    
    
     a
    
    
     的距离为
    
    
     c
    
    
     的话。则有：
    
    
    
     
      {
     
     
      
       
        
         
          
           (
          
          
           x
          
          
           −
          
          
           
            x
           
           
            1
           
          
          
           
            )
           
           
            2
           
          
          
           +
          
          
           (
          
          
           y
          
          
           −
          
          
           
            y
           
           
            1
           
          
          
           
            )
           
           
            2
           
          
          
           =
          
          
           
            c
           
           
            2
           
          
         
        
       
      
      
       
        
         
          
           (
          
          
           y
          
          
           −
          
          
           
            y
           
           
            1
           
          
          
           )
          
          
           /
          
          
           (
          
          
           x
          
          
           −
          
          
           
            x
           
           
            1
           
          
          
           )
          
          
           =
          
          
           k
          
         
        
       
      
     
    
    
     点
    
    
     a
    
    
     已知，距离
    
    
     c
    
    
     已知，斜率
    
    
     k
    
    
     已知
    
    
    
     联立方程可以解得：
    
    
    
     
      {
     
     
      
       
        
         
          
           x
          
          
           =
          
          
           ±
          
          
           
            c
           
           
            
             
              1
             
             
              +
             
             
              
               k
              
              
               2
              
             
            
           
          
          
           +
          
          
           
            x
           
           
            1
           
          
         
        
       
      
      
       
        
         
          
           y
          
          
           =
          
          
           ±
          
          
           
            
             c
            
            
             k
            
           
           
            
             
              1
             
             
              +
             
             
              
               k
              
              
               2
              
             
            
           
          
          
           +
          
          
           
            y
           
           
            1
           
          
         
        
       
      
     
    
   
   
     点 a 坐标为 (x_1, y_1), 点b坐标为(x_2, y_2) \\ 现在，a b的距离 = (x_2 - x_1)^2 +(y_2 - y_1)^2 \\ 直线 ab的斜率为 k = (y_2-y_1) / (x_2-x_1) \\ 现在点c(x, y)在ab上，若与a的距离为c的话。则有：\\ \begin{cases} (x - x_1)^2 +(y - y_1)^2 = c^2 \\ (y-y_1) / (x-x_1) = k \end{cases} 点a已知，距离c已知，斜率k已知 \\ 联立方程可以解得：\\ \begin{cases} x = \pm \frac{c}{\sqrt{1 + k^2}} +x_1\\ y = \pm \frac{c k}{\sqrt{1 + k^2}} +y_1 \end{cases} 
   
  
 点a坐标为(x1,y1),点b坐标为(x2,y2)现在，ab的距离=(x2−x1)2+(y2−y1)2直线ab的斜率为k=(y2−y1)/(x2−x1)现在点c(x,y)在ab上，若与a的距离为c的话。则有：{(x−x1)2+(y−y1)2=c2(y−y1)/(x−x1)=k点a已知，距离c已知，斜率k已知联立方程可以解得：{x=±1+k2c+x1y=±1+k2ck+y1

直线和圆相交的点圆两个，只有一个是合法的，这里只需要判断一下即可

bool__graphLine__containsLine(QPointF begin, QPointF end, QPointF now){
    QLineF a(begin, end);
    QLineF b(begin, now);
    QLineF c(now, end);if(fabs(a.length()- b.length()- c.length())<1e-6)returntrue;returnfalse;}

计算出圆与直线的交点之后，绘制两根直线，分别向上和向下偏移30°来充当箭头即可。

void graphLine::paintArrow(graphNode* begin, graphNode* end, QPainter* painter){auto r_begin = begin->getPoint()+ begin->pos();auto r_end = end->getPoint()+ end->pos();
    QLineF lines(r_begin, r_end);auto length = end->getR()+ end->getRoundWidth()/2;// 宽度是内圈外圈各渲染一部分
    qreal dx, dy;if(fabs(lines.dx())<1e-6){
        dx =0;
        dy = length;}else{auto k = lines.dy()/ lines.dx();
        qreal base =sqrt(k * k +1);
        dx = length / base;
        dy = length * k / base;}

    QPointF dis(dx, dy);
    QPointF now;if(__graphLine__containsLine(r_begin, r_end,QPointF(r_end + dis))){
        now =QPointF(r_end + dis);}else{
        now =QPointF(r_end - dis);}

    QLineF arrowHead(now, r_begin);
    arrowHead.setLength(10+ end->getRoundWidth());

    arrowHead.setAngle(arrowHead.angle()-30);// 上方
    painter->drawLine(arrowHead);

    arrowHead.setAngle(arrowHead.angle()+60);// 下方
    painter->drawLine(arrowHead);}

知道如何绘制箭头之后，和绘制直线组合起来，就可以了；

paint

完整代码

void graphLine::paint(QPainter *painter,const QStyleOptionGraphicsItem *option, QWidget *widget){auto r_begin = begin->getPoint()+ begin->pos();auto r_end = end->getPoint()+ end->pos();
    QLineF lines(r_begin, r_end);setLine(lines);

    QPen pen;
    pen.setWidth(2);if(isSelected()){
        pen.setColor(QColor((color.red()+125)%255,(color.green())%255,(color.blue()+125)%255));}else{
        pen.setColor(color);}

    painter->setPen(pen);
    painter->setRenderHint(QPainter::HighQualityAntialiasing);
    painter->drawLine(line());switch(lineType){case LeftToRight:paintArrow(begin, end, painter);break;case RightToLeft:paintArrow(end, begin, painter);break;case TwoWayArrow:paintArrow(begin, end, painter);paintArrow(end, begin, painter);break;case NoArrow:;default:;}}

在这里，添加点我选择使用右键单击添加，连接点是选择两个点就自动添加一根线

这些处理将直接在 view类里面进行处理，因此，我自定义了一个graph类

classgraph:publicQGraphicsView{
    Q_OBJECT
public:enumSelectItemMode{
        Line,
        Node,

        None =10086,};explicitgraph(QWidget *parent =nullptr);
    QList<graphLine*>Lines();
    QList<graphNode*>Nodes();voidsetMode(SelectItemMode);private:
    SelectItemMode selectItemMode;
    QSet<graphLine*> graphLines;
    QSet<graphNode*> graphNodes;
    QHash<graphNode*, QSet<graphNode*>> graphMap;private:voidmouseLButtonClick(QMouseEvent *event);voidmouseRButtonClick(QMouseEvent *event);protected:voidmousePressEvent(QMouseEvent *event)override;voidmouseMoveEvent(QMouseEvent *event)override;voidmouseReleaseEvent(QMouseEvent *event)override;
signals:voidmouseClickEvent(QPoint point);voidmouseMoveEvent(QPoint point);voidselectItem(QGraphicsItem *);// QWidget interfaceprotected:voidresizeEvent(QResizeEvent *event)override;voidpaintEvent(QPaintEvent *event)override;private slots:voidon_scene_select_change();voidon_selection_change(QGraphicsItem *, QGraphicsItem *, Qt::FocusReason);};

添加点

graph类重写

 mousePressEvent

方法。

void graph::mousePressEvent(QMouseEvent *event){switch(event->button()){case Qt::MouseButton::RightButton:mouseRButtonClick(event);break;default:QGraphicsView::mousePressEvent(event);}}

然后在

mouseRButtonClick

中处理右键事件

void graph::mouseRButtonClick(QMouseEvent *event){auto pointScene =mapToScene(event->pos());auto item =newgraphNode(pointScene,20,QString("A")));
    item->setFlag(QGraphicsItem::ItemIsMovable,true);if(selectItemMode == Node){
        item->setFlags( item->flags()|
                        QGraphicsItem::ItemIsFocusable |
                        QGraphicsItem::ItemIsSelectable);}scene()->addItem(item);
    graphNodes.insert(item);}

添加线

添加线需要通过处理

selectionChanged

connect(scene(),SIGNAL(selectionChanged()),this,SLOT(on_scene_select_change()));

当选择的item为2时，则连接一条直线

void graph::on_scene_select_change(){// mode select graphNodeauto list =scene()->selectedItems();if(selectItemMode == Node){staticdecltype(list) old_list;if(list.size()>2){scene()->clearSelection();return;}if(list.size()==2){auto a{dynamic_cast<graphNode*>(list[0])},
            b{dynamic_cast<graphNode*>(list[1])};if(old_list[0]!= list[0]) std::swap(a, b);if(graphMap[a].contains(b))return;// 两点之间有线不需要连接Ⅰ
            graphMap[a].insert(b);
            graphMap[b].insert(a);auto now =newgraphLine(a, b);if(selectItemMode == Line){
                now->setFlags( now->flags()|
                               QGraphicsItem::ItemIsFocusable |
                               QGraphicsItem::ItemIsSelectable);}scene()->addItem(now);
            graphLines.insert(now);}
        old_list = list;}elseif(selectItemMode == Line){if(list.size()>1){scene()->clearSelection();return;}}auto item =scene()->mouseGrabberItem();
    emit selectItem(item);}

到这里，基本上，核心的东西就完成了，剩下的是ui界面了。

我的ui界面比较丑，大概长这样：

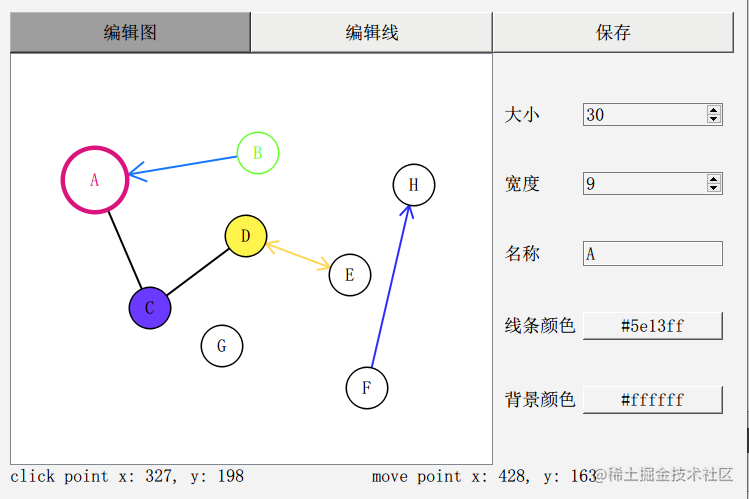
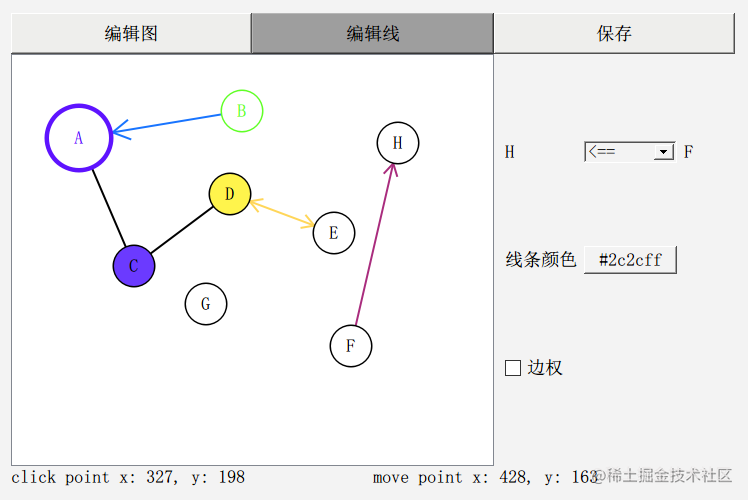
这就是一个最基本的图编辑器了

{来自 amjieker }

标签： qt ui 开发语言

本文转载自: https://blog.csdn.net/qq_51986723/article/details/128708495
版权归原作者 AMjieker 所有，如有侵权，请联系我们删除。

利用QT 的 Graphics View 系统实现一个简易的 Graph Editor

如何绘制点

如何绘制线

不带箭头

带箭头

添加点

添加线

发表评论