信息与网络安全
文章目录
第一章 概述
1.1 基本概念
信息安全是指信息网络中的硬件、软件及其系统中的数据受到保护，不受偶然的或者恶意的原因而遭到破坏、更改、泄露、否认等，系统连续可靠正常的运行，信息服务不中断。
信息安全威胁是指某些因素（人、物、事件、方法等）对信息系统的安全使用可能构成的危害。
1.2 攻击
概念
攻击：仅仅发生在入侵行为完全完成，且入侵者已进入目标网络内的行为称为攻击。但更为积极的观点是：所有可能使一个网络受到破坏的行为都称为攻击。即从一个入侵者开始在目标机上工作的那个时刻起，攻击就开始了。
分类
- 泄漏信息：指敏感数据在有意或无意中被泄漏出去或丢失。
- 破坏信息：以非法手段窃得对数据的使用权，删除、修改、插入或重发某些重要信息，以取得有益于攻击者的响应； 恶意添加，修改数据，以干扰用户的正常使用。
- 拒绝服务：它不断对网络服务系统进行干扰，影响正常用户的使用，甚至使合法用户被排斥而不能进入计算机网络系统或不能得到相应的服务。
常用手段
- 口令入侵
- 后门软件手段
- 监听法
- E-mail技术
- 电子欺骗
- DoS攻击（拒绝服务攻击）
1.3 信息安全的目的
信息安全核心三要素（也称CIA三要素）
- 机密性
- 完整性
- 可用性
信息安全典型技术
- 信息加密技术（基于密码学）
- 防火墙技术
- 漏洞扫描技术
- 入侵检测技术
- 防病毒技术
- 网络安全隧道技术（VPN）
第二章 信息加密技术
2.1 信息安全与密码学
密码学基本概念
密码学（Cryptology）是结合数学、计算机科学、电子与通信等学科于一体的交叉学科，研究信息系统安全的科学。起源于保密通信技术。具体来讲，研究信息系统安全保密和认证的一门科学。
密码学是信息安全的核心和关键技术
密码学发展历史
- 古典密码- 手工密码- 机械密码
- 近代密码1976年提出公钥加密体制
- 现代密码
2.2 密码学经典例子
古典密码
置换密码：根据一定的规则重新排列明文，打破明文的结构特性。其特点是保持明文的所有字符不变，只是打乱了明文字符的位置和次序。
典型例子：
- Caesar（凯撒密码）原理 ¶凯撒密码（Caesar）加密时会将明文中的 每个字母 都按照其在字母表中的顺序向后（或向前）移动固定数目（循环移动）作为密文。例如，当偏移量是左移 3 的时候（解密时的密钥就是 3）：
明文字母表：ABCDEFGHIJKLMNOPQRSTUVWXYZ密文字母表：DEFGHIJKLMNOPQRSTUVWXYZABC使用时，加密者查找明文字母表中需要加密的消息中的每一个字母所在位置，并且写下密文字母表中对应的字母。需要解密的人则根据事先已知的密钥反过来操作，得到原来的明文。例如：明文：THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG密文：WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ例题已知密文为vzsx，位移量为3，求明文？解：第一步，写出密文中字母对应的位置（下标），比如说a在字母表中为第一位，就记作1（记作0也可以,最后一个字母z = 25） 所以我们可以写出v = 22,z = 26,s = 19,x = 24 第二步，因为位移量为3，所以我们将以上数字都减3，即19,23,16,21 第三步，将以上数字还原为字母，19对应s,23对应w,16对应p,21对应u,我们就解出了明文swpu.
代换密码：代换，就是将明文中的一个字母由其它字母、数字或者符号替代的一种方法。
常见代换密码
- 单表代换（caesar，仿射密码（考试不要求））
- 多表代换（PlayFair,vigenere(维吉尼亚密码),Hill(希尔密码)）
典型例子：
- PlayFair
原理 ¶
Playfair 密码（Playfair cipher or Playfair square）是一种替换密码，1854 年由英国人查尔斯 · 惠斯通（Charles Wheatstone）发明，基本算法如下：
- 选取一串英文字母，除去重复出现的字母，将剩下的字母逐个逐个加入 5 × 5 的矩阵内，剩下的空间由未加入的英文字母依 a-z 的顺序加入。注意，将 q 去除，或将 i 和 j 视作同一字。
- 将要加密的明文分成两个一组。若组内的字母相同，将 X（或 Q）加到该组的第一个字母后，重新分组。若剩下一个字，也加入 X 。
- 在每组中，找出两个字母在矩阵中的地方。 - 若两个字母不同行也不同列，在矩阵中找出另外两个字母（第一个字母对应行优先），使这四个字母成为一个长方形的四个角。- 若两个字母同行，取这两个字母右方的字母（若字母在最右方则取最左方的字母）。- 若两个字母同列，取这两个字母下方的字母（若字母在最下方则取最上方的字母）。
新找到的两个字母就是原本的两个字母加密的结果。
以 playfair example 为密匙，得
P L A Y F
I R E X M
B C D G H
K N O Q S
T U V W Z
要加密的讯息为 Hide the gold in the tree stump
HI DE TH EG OL DI NT HE TR EX ES TU MP
就会得到
BM OD ZB XD NA BE KU DM UI XM MO UV IF
说人话版本
- 先选一个密钥,比如说密钥是NSSCTF，然后我们把这个密钥填进一个5x5的表格里面，重复的字母不要。NSCTF
- 剩下的格子怎么填呢？按字母表A-Z依次填，还是老规矩，重复的字母不要。还要满足一个要求：要么不要Q这个字母，要么把I/J写在一起，选一个就行。NSCTFABDEGHI/JKLMOPQRUVWXYZ这样就填好了
- 比如说我们要加密的句子是：“Reach the highest City”，我们把它两两分组
RE AC HT HE HI GH ES TC IT Y这里Y落单了对吧？落单的字母我们在后面补X - 我们来看第二组字母的相对位置
A和C既不在同一行也不在同一列对吧？这个时候我们就要找两个字母让他们连起来是一个长方形，这里显然是N,D两个字母，但是先后顺序是什么呢？因为这一组字母中A在前面，所以我们以A这一行优先，跟R同一行的是D，所以第一组密文为DN - 再来看一组同行的例子HI
对于这种情况，我们就去找他后面的那个字母，H -> I/J ，I/J -K ,所以密文是 I/J K - 再来看一组同列的例子RE
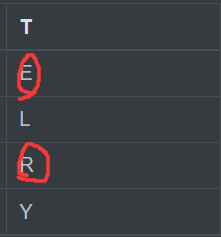还是去找他后面的字母 R -> Y,E -> L，密文为YL - 这就是PlayFair的加密过程
Playfair密码的优点（非重点）
Playfair密码与简单的单一字母替代法密码相比有了很大的进步
虽然仅有26个字母，但有26×26＝676种字母对，因此，识别字母对要比单个字母要困难得多。
一个明文字母有多种可能的代换密文字母，使得频率分析困难的多(hs成为BP,hq成为YP)
Playfair密码过去长期被认为是不可破的。
- vigenere（维吉尼亚密码）原理 ¶维吉尼亚密码（Vigenere）是使用一系列凯撒密码组成密码字母表的加密算法，属于多表密码的一种简单形式。
下面给出一个例子明文：come greatwall密钥：crypto首先，对密钥进行填充使其长度与明文长度一样。明文comegreatwall密钥cryptocryptoc其次，查表得密文
明文：come greatwall密钥：crypto密文：efkt zferrltzn说人话版本和凯撒密码差不多，先把字母转化为下标的形式（a = 0,b = 1…）比如说明文是NSSCTF,密钥是SWPU，怎么加密呢？1. 先将字母转为对应下标。(引用老师的一张图)
NSSCTF -> 13 18 18 2 19 5SWPU -> 18 22 15 202. 我们将密钥写在明文下面，填满为止NSSCTFSWPUSW3. 满足以下公式 加 密 ： c i = p i + k i ( m o d 26 ) 解 密 ： p i = c i − k i ( m o d 26 ) 加密：c_i = p_i + k_i (mod26)\ 解密：p_i = c_i - k_i(mod 26) 加密：ci=pi+ki(mod26)解密：pi=ci−ki(mod26) 什么意思呢，我们刚刚不是将字母转成数字了吗，我们来运算一下，密文的第一个字母为(13 + 18) % 26 = 5 -> F第二个字母为 （18 + 22） % 26 = 14 -> O…最终的密文为FOHWLB4. 怎么解密呢，我们用解密公式演算一下。明文的第一个字母为（5 - 18）% 26 = 13 -> N,第二个字母为(14 - 22) % 26 = 18 -> S…最终明文为NSSCTF - Hill（希尔密码）原理 ¶希尔密码（Hill）使用每个字母在字母表中的顺序作为其对应的数字，即 A=0，B=1，C=2 等，然后将明文转化为 n 维向量，跟一个 n × n 的矩阵相乘，再将得出的结果模 26。注意用作加密的矩阵（即密匙）在 Zn26必须是可逆的，否则就不可能解码。只有矩阵的行列式和 26 互质，才是可逆的。下面举一个例子
明文：ACT将明文化为矩阵。 [ 0 2 19 ] \begin{bmatrix} 0\ 2\ 19\ \end{bmatrix} ⎣⎡0219⎦⎤ 假设密钥为： [ 6 24 1 13 16 10 20 17 15 ] \begin{bmatrix} 6 & 24 & 1\ 13 & 16&10\ 20 & 17 & 15\ \end{bmatrix} ⎣⎡6132024161711015⎦⎤加密过程为： [ 6 24 1 13 16 10 20 17 15 ] [ 0 2 19 ] = [ 67 222 319 ] ( m o d 26 ) = [ 15 14 7 ] \begin{bmatrix} 6 & 24 & 1\ 13 & 16&10\ 20 & 17 & 15\ \end{bmatrix} \begin{bmatrix} 0\ 2\ 19\ \end{bmatrix} = \begin{bmatrix} 67\ 222\ 319\ \end{bmatrix} (mod 26) = \begin{bmatrix} 15\ 14\ 7\ \end{bmatrix} ⎣⎡6132024161711015⎦⎤⎣⎡0219⎦⎤=⎣⎡67222319⎦⎤(mod26)=⎣⎡15147⎦⎤密文即为密文：POH可能有些同学忘记线性代数怎么算了，我们这里来算一遍我们用密钥矩阵的第一行乘明文矩阵，就是6*0 + 24*2 + 1*19 = 67第二行乘明文矩阵：13*0 + 16*2 + 10*19 = 222第三行乘明文矩阵：20*0 + 17*2 + 15*19 = 319该矩阵是3 * 3 X 3 * 1 = 3 * 1所以最后得到的矩阵是三行一列的矩阵，然后再对26取模得到的数字就是该字母的下标。
2.3 密码学基本概念
密码技术
- 密码技术的基本思想是伪装信息。
- 伪装就是对数据施加一种可逆的数学变换，伪装前的数据称为明文，伪装后的数据称为密文，伪装的过程称为加密，去掉伪装恢复明文的过程称为解密。加密和解密的过程要在密钥的控制下进行。
- 密码学(Cryptology)：研究信息系统安全保密的科学。它包含两个分支： - 密码编码学- 密码分析学
密码学中一些术语的解释
一个密码（加密）系统是由明文、密文、加密算法、解密算法、密钥五部分组成。
- 明文M：作为加密输入的原始信息，即消息的原始形式
- 密文C：明文经加密变换后的结果，即消息被加密处理后的形式
- 密钥K：是参与密码变换的参数
- 加密算法E：是将明文变换为密文的变换函数，相应的变换过程称为加密，即编码的过程
- 解密算法D：是将密文恢复为明文的变换函数，相应的变换过程称为解密
数据安全基于密钥而不是算法的保密 （这句话是重点）
对于一个密码体制，其算法是可以公开的，让所有人来使用、研究。但具体对于某次加密过程中所使用的密钥，则是保密的。
按密钥的使用方式分类
- 非对称加密（公钥密码体制）用于加密的密钥与用于解密的密钥是不同的，而且从加密的密钥无法推导出解密的密钥。用公钥KP对明文加密可表示为：EKP(M)=C用相应的私钥KS对密文解密可表示为：DKS©=M
- 对称加密用于加密数据的密钥和用于解密数据的密钥相同，或者二者之间存在着某种明确的数学关系。加密：EK(M)=C解密：DK©=M
2.4 对称密码体制
概念
说白了就是加密的密钥和解密的密钥是一样的。
安全性
- 加密算法足够安全
- 密钥的安全性（如果密钥太简单，可以轻易被计算机爆破出来）
优缺点
优点：加解密速度快、保密度高
缺点：如何安全传递密钥（如果密钥在网络上被截获了就GG）、多人分发需要的密钥数量会急速增加
分类
- 序列密码对明文的单个位（或字节）进行运算的算法，也称流密码需要注意的是，流加密目前来说都是对称加密。伪随机数生成算法生成的序列的随机性越强，明文中的统计特征被覆盖的更好。流密码加解密非常简单，在已知明文的情况下，可以非常容易地获取密钥流。流密码的关键在于设计好的伪随机数生成器。一般来说，伪随机数生成器的基本构造模块为反馈移位寄存器。当然，也有一些特殊设计的流密码，比如 RC4。
- 分组密码把明文信息划分成不同的块（或小组）结构，分别对每个块（或小组）进行加密和解密其实，我们也可以把块加密理解一种特殊的替代密码，但是其每次替代的是一大块。而正是由于一大块，明文空间巨大，而且对于不同的密钥，我们无法做一个表进行对应相应的密文，因此必须得有 复杂 的加解密算法来加解密明密文。而与此同时，明文往往可能很长也可能很短，因此在块加密时往往需要两个辅助- padding，即 padding 到指定分组长度- 分组加密模式，即明文分组加密的方式。所以分组密码有以下要求- 分组长度足够大- 密钥量空间足够大- 加密变换足够复杂- 加密和解密运算简单，一般采用加法、乘法、异或和移位等简单的运算- 加密和解密的逻辑结构最好一致。
2.5 对称加密算法
DES、AES
太难了我不会。。
2.6 非对称（公钥）加密算法
基本原理
基于单向陷门函数
什么是单向陷门函数呢？拿RSA算法举例，给你两个质数，你要计算他们的乘积是很容易的吧，但是如果给你一个数让你计算他的两个质因数就是很困难的，可以自己写代码实现一下，这就是单向陷门函数，正向计算很容易，反过来就困难了，公钥密码的安全性正是基于这样的数学难题
具体的实现步骤在下文以RSA算法为例
应用场景
- 保护数据机密性
- 实现认证性/消息完整性（数字签名算法）
- 解决密钥分配问题
RSA
介绍
RSA 加密算法是一种非对称加密算法。在公开密钥加密和电子商业中 RSA 被广泛使用。RSA 是 1977 年由罗纳德 · 李维斯特（Ron Rivest）、阿迪 · 萨莫尔（Adi Shamir）和伦纳德 · 阿德曼（Leonard Adleman）一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。
RSA 算法的可靠性由极大整数因数分解的难度决定。换言之，对一极大整数做因数分解愈困难，RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话，那么用 RSA 加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。如今，只有短的 RSA 密钥才可能被强力方式解破。到 2017 年为止，还没有任何可靠的攻击 RSA 算法的方式。
基本原理
公钥与私钥的产生 ¶
- 随机选择两个不同大质数 p和 q，计算 N=p×q
- 根据欧拉函数，求得 φ(N)=φ§φ(q)=(p−1)(q−1)
- 选择一个小于 φ(N)的整数 e，使 e 和 φ(N) 互质。并求得 e 关于 φ(N) 的模反元素，命名为 d，有 ed≡1(modφ(N))
- 将 p和 q的记录销毁,此时，(N,e)是公钥，(N,d) 是私钥。
消息加密
c = m^e mod N
m = c^d mod N
一些数学名词的解释
- 质数（素数）：就是它只能被1和它本身整除的数
- 欧拉函数φ(N)：就等于(p-1)*(q-1)
- 模运算- 模运算与基本四则运算有些相似，但是除法除外。其规则如下：- - (a + b) % p = (a % p + b % p) % p- (a - b) % p = (a % p - b % p) % p- (a * b) % p = (a % p * b % p) % p- a ^ b % p = ((a % p) ^ b) % p- 结合律- - ((a + b) % p + c) = (a + (b + c) % p) % p- ((a * b) % p * c) = (a * (b * c) % p) % p- 交换律- - (a + b) % p = (b + a) % p- (a * b) % p = (b * a) % p- 分配律- - (a + b) % p = (a % p + b % p) % p- ((a + b) % p * c) % p = ((a * c) % p + (b * c) % p
- 模逆元逆元是指在数学领域群G中任意一个元 a，都在G中有唯一的逆元a’，具有性质 a · a’ = a’ · a = e ( · 为该群中定义的运算)。其中，e为该群的单位元。逆元其实是加法中的相反数以及乘法中的倒数的拓展思想。在模运算中，单位元便是1。a mod p的逆元便是可以使 a * a’ mod p = 1 的最小a’。因为 b’ 为 b 的逆元，b * b’ mod p = 1；所以 (a / b) mod p = (a * b’) mod p ，但要求a | b；这样我们便可以应用 (a * b) % p = (a % p * b % p) % p 这一条性质缩小中间运算结果了。
以代码举例
我们用python来实现一遍加解密过程
from Crypto.Util.number import*import gmpy2
# 选取两个大素数p,q
p = getPrime(128)
q = getPrime(128)# 计算出N
N = p * q
# 计算欧拉函数phiN
phiN =(p -1)*(q -1)# 选取一个质数e，要求e和phiN互质(phiN不能整除e)
e =17# 计算私钥d,这里实际是用到了扩展欧几里得算法求模逆元，后面讲
d = gmpy2.invert(e, phiN)# 这是我们要加密的明文
m ='this is a test'# 我们先将明文转成字节类型，再转化成十进制数字
m = bytes_to_long(m.encode())# 进行加密 c = m^e mod N
c =pow(m, e, N)print(c)# 进行解密 m = c^d mod N
m =pow(c, d, N)# 此时明文是十进制数字类型，转成字节类型
m = long_to_bytes(m)print(m)
d怎么求？
我们前面已经知道d的求解是基于这个公式：ed≡1(modφ(N)),首先≡这个符号是什么意思？这是数论中的同余符号，意思是两个整数除以同一个整数，若得相同余数，则二整数同余，这个公式如果要转化为人能看懂的东西，怎么转化呢？对于数字较小的场景，可以用这个公式ed + phiNy = 1,其中y为负整数，d为正整数，可以从y = -1开始，来解d是否为正整数，以上次的作业为例
设通信双方使用RSA加密体制，接收方的公开钥是(n, e) = (35，5)，接收到的密文是C = 10，求明文M。
n = 35 ,分解为两个素数相乘的结果为5*7，计算欧拉函数phiN = （5-1）*（4-1） = 24，此时用我们上面的公式解d
即ed+phiNy = 1 -> 5*d + 24*y = 1
取y = -1，z则方程变成5*d - 24 = 1 -> d = 5
d刚好是正整数5，然后根据公式m = c^d mod N -> M = 10^5 mod 35 = 5
如果数字稍微大一点，就需要用扩展欧几里得算法了
扩展欧几里得算法
以老师ppt上的例子为例
e = 1234 ,phiN = 11111,求d=？
首先，如果这个d存在的话，我们用phiN除以e（保留余数） 即11111 / 1234 = 9 ...5 -> 11111 = 9*1234 + 5
再算1234 / 上一次的余数5 = 246 ...4 -> 1234 = 246*5 + 4
5 / 4 = 1...1 -> 5 = 4*1 + 1
算到除数为1就结束了，然后我们倒过来写这串表达式
1 = 5-1*4
4 = 1234-246*5
5 = 11111-9*1234
带进去就得到了1 = (5-1*(1234-246*5))
根据ed = 1 mod phin
即1234*d = (5-1*(1234-246*5)) mod phin
化简一下
错误版本！！！
1234
∗
d
=
(
5
−
1
∗
(
1234
−
246
∗
5
)
)
m
o
d
p
h
i
n
=
(
5
−
1234
+
246
∗
5
)
m
o
d
p
h
i
n
=
(
247
∗
5
−
1234
)
m
o
d
p
h
i
n
=
[
247
∗
(
11111
−
9
∗
1234
)
−
1234
]
m
o
d
p
h
i
n
=
(
11111
∗
247
−
9
∗
247
∗
1234
−
1234
)
m
o
d
p
h
i
n
=
(
11111
∗
247
−
2224
∗
1234
)
m
o
d
p
h
i
n
∵
p
h
i
n
=
11111
,
11111
∗
247
m
o
d
11111
=
0
∴
1234
∗
d
=
−
2224
∗
1234
m
o
d
11111
这
里
我
写
错
了
兄
弟
们
！
！
最
后
一
步
是
对
−
2224
取
模
d
=
2224
是
错
的
！
！
\begin{aligned} 1234*d &= (5-1*(1234-246*5))\ mod \ phin\\ &=(5-1234+246*5)\ mod \ phin\\ &=(247*5 - 1234) \ mod \ phin\\ &=[247*(11111-9*1234) - 1234] \ mod \ phin\\ &=(11111*247-9*247*1234-1234) \ mod \ phin\\ &=(11111*247 - 2224*1234) \ mod \ phin\\ &\because phin\ = 11111,11111*247 \ mod \ 11111 = 0\\ &\therefore \ 1234*d= -2224*1234 \ mod \ 11111\\ &这里我写错了兄弟们！！\\ &最后一步是对-2224取模\\ d &=2224是错的！！ \end{aligned}
1234∗dd=(5−1∗(1234−246∗5)) mod phin=(5−1234+246∗5) mod phin=(247∗5−1234) mod phin=[247∗(11111−9∗1234)−1234] mod phin=(11111∗247−9∗247∗1234−1234) mod phin=(11111∗247−2224∗1234) mod phin∵phin =11111,11111∗247 mod 11111=0∴ 1234∗d=−2224∗1234 mod 11111这里我写错了兄弟们！！最后一步是对−2224取模=2224是错的！！
负数取模
x
m
o
d
y
=
x
−
y
∗
[
x
y
]
(
向
下
取
整
)
=
−
2224
−
11111
∗
(
−
2224
11111
)
=
−
2224
+
11111
=
8887
∴
d
=
8887
\begin{aligned} x \ mod \ y &= x - y * [\frac{x}{y}](向下取整)\\ &= -2224 - 11111 * (\frac{-2224}{11111})\\ &= -2224 + 11111\\ &= 8887\\ \therefore d&=8887 \end{aligned}
x mod y∴d=x−y∗[yx](向下取整)=−2224−11111∗(11111−2224)=−2224+11111=8887=8887
感谢同学指出的错误
如何计算m^emod n
使用快速幂取模算法，原理我没研究过，就不班门弄斧了，以老师ppt上的例子为例
采用快速取模指数算法求c1=m1^e(mod n) =104^13 mod 2537 的值？
我们来解读这段代码
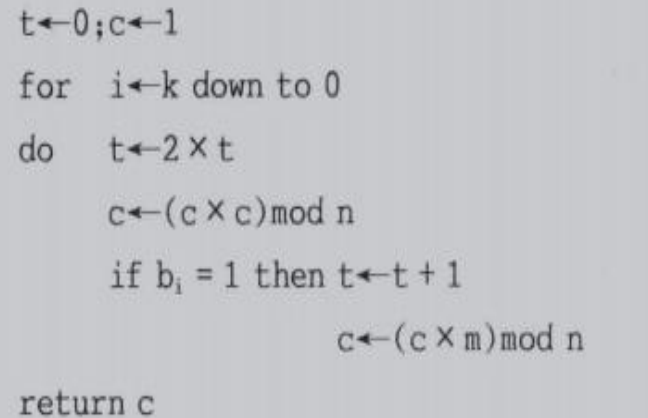
第一轮代码
t
=
0
，
c
=
1
,
i
=
3
t
=
t
∗
2
(
t
=
0
)
c
=
c
∗
c
m
o
d
2537
(
c
=
1
)
i
f
b
3
=
=
1
(
满
足
)
:
t
=
t
+
1
(
t
=
1
)
c
=
1
∗
104
m
o
d
2537
(
c
=
104
)
\begin{aligned} &t=0，c=1,i=3\\ &t = t*2\ (t=0)\\ &c = c*c \ mod \ 2537 \ (c=1)\\ &if \ b_3 == 1(满足):\\ &t = t+1 \ (t=1)\\ &c = 1*104\ mod\ 2537\ (c=104)\\ \end{aligned}
t=0，c=1,i=3t=t∗2 (t=0)c=c∗c mod 2537 (c=1)if b3==1(满足):t=t+1 (t=1)c=1∗104 mod 2537 (c=104)
第二轮代码
t
=
1
，
c
=
104
,
i
=
2
t
=
t
∗
2
(
t
=
2
)
c
=
c
∗
c
m
o
d
2537
(
c
=
668
)
i
f
b
2
=
=
1
(
满
足
)
:
t
=
t
+
1
(
t
=
3
)
c
=
668
∗
104
m
o
d
2537
(
c
=
973
)
\begin{aligned} &t=1，c=104,i=2\\ &t = t*2\ (t=2)\\ &c = c*c \ mod \ 2537 \ (c=668)\\ &if \ b_2 == 1(满足):\\ &t = t+1 \ (t=3)\\ &c = 668*104\ mod\ 2537\ (c=973)\\ \end{aligned}
t=1，c=104,i=2t=t∗2 (t=2)c=c∗c mod 2537 (c=668)if b2==1(满足):t=t+1 (t=3)c=668∗104 mod 2537 (c=973)
第三轮代码
t
=
3
，
c
=
973
,
i
=
1
t
=
t
∗
2
(
t
=
6
)
c
=
c
∗
c
m
o
d
2537
(
c
=
428
)
i
f
b
1
=
=
1
(
不
满
足
)
:
\begin{aligned} &t=3，c=973,i=1\\ &t = t*2\ (t=6)\\ &c = c*c \ mod \ 2537 \ (c=428)\\ &if \ b_1 == 1(不满足):\\ \end{aligned}
t=3，c=973,i=1t=t∗2 (t=6)c=c∗c mod 2537 (c=428)if b1==1(不满足):
第四轮代码
t
=
6
，
c
=
428
,
i
=
1
t
=
t
∗
2
(
t
=
12
)
c
=
c
∗
c
m
o
d
2537
(
c
=
520
)
i
f
b
1
=
=
1
(
满
足
)
:
t
=
t
+
1
(
t
=
13
)
c
=
520
∗
104
m
o
d
2537
(
c
=
803
)
\begin{aligned} &t=6，c=428,i=1\\ &t = t*2\ (t=12)\\ &c = c*c \ mod \ 2537 \ (c=520)\\ &if \ b_1 == 1(满足):\\ &t = t+1 \ (t=13)\\ &c = 520*104\ mod\ 2537\ (c=803)\\ \end{aligned}
t=6，c=428,i=1t=t∗2 (t=12)c=c∗c mod 2537 (c=520)if b1==1(满足):t=t+1 (t=13)c=520∗104 mod 2537 (c=803)
此时代码运行完毕，c就是我们最终的结果803，我们用python验证一下
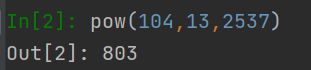
正确的。
RSA算法的安全性
RSA算法的安全性是基于大整数分解的难题，所以攻击方式也很简单粗暴，因为公钥是公开的，n = p*q,e已知，e * d = 1 mod phiN,所以我们只要能分解N为两个素数p,q,就能破解出d，以下介绍几种常见的攻击方式（考试应该不会考，感兴趣的同学可以看看）
- 暴力分解可以使用yafu这款工具，使用方式如下：
factor()函数，参数是你要分解的数，分解结果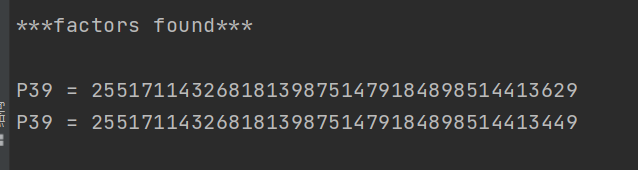
- 共模攻击攻击条件 ¶当两个用户使用相同的模数 N、不同的私钥时，加密同一明文消息时即存在共模攻击。攻击原理 ¶设两个用户的公钥分别为 e1 和 e2，且两者互质。明文消息为 m，密文分别为：c1=m^e1modNc2=m^e2modN当攻击者截获 c1和 c2 后，就可以恢复出明文。用扩展欧几里得算法求出 re1+se2=1modn 的两个整数 r 和 s，由此可得：cr1cs2≡mre1mse2modn ≡m(re1+se2)modn ≡mmodn代码实现
import gmpy2from Crypto.Util.number import*import sysimport binasciisys.setrecursionlimit(1000000)defegcd(a, b):if a ==0:return b,0,1else: g, y, x = egcd(b % a, a)return g, x -(b // a)* y, ydefmodinv(a, m): g, x, y = egcd(a, m)if g !=1:raise Exception('modular inverse does not exist')else:return x % me1=11085119e2=9190891c1=95802654515220808092268214474187396521084451096344242384608341887872702782290828816410697000941719590683107309925626046620976811737721800675450679405244429986569795481605454039209952126809031130572473139930816538229894404952230488471032140646478701800056893148667212842612771202600961005473843628543807576281789895225835535784697736508073945719275038557487868878529515390772120147529559169015697350455629223009240723598393858545457969371930544199690993535334876475403150437839542800975521617422860338848091674741969911523078015503201576312728495586541524742813914511874800249782937376857844116922101278519019905656c2=3416491037051012037012939467509239901806773704813403690354665798385393352563464881951974370241490158340518054254272653945115953885714558484209218930263157351532115665285897349811123032115674114898665575574766463243374363257317681664993192800007993550862200779683771913077545068424882032234253291268535634268961963331194864584762384909221320182259740507346013284854960761334127762166029934217852574313390086250095835456562558784241431962078316429891165585256316059135820341820577055463538905611710942258927193841136883208222189378113731075034150942645682604044709019188371375927920059650896388569726047796473642120516n=14129293489067735497835891913264472598235466604403612336006623107595438847067174121647397164285682966224208717924641463649550121959767200641904319708499428189547128930841593746541543006588640663582633284897803861765348725014771273881669308132805898675778540187033021154036594235144466199756659779020003038086388668345228666342476638806787610903886102447352152686433249208463728111915471444774767068270174477504938000592014963263451887545807532838102764510144961264142596092689778866428703620285541772740910077089202507682976490982442688834900108765694679294561760962915865812857912066376963510711262436193703892095683s = egcd(e1, e2)s1 = s[1]s2 = s[2]if s1 <0: s1 =- s1 c1 = modinv(c1, n)elif s2 <0: s2 =- s2 c2 = modinv(c2, n)m =(pow(c1, s1, n)*pow(c2, s2, n))% nprint(long_to_bytes(m))m = gmpy2.iroot(m,9)[0]print(long_to_bytes(m)) - e与phiN不互素
- p和q相差过大或过小就是暴力分解的那个例子，p和q十分接近
- 小明文攻击如果明文过小的话，导致明文的e次方仍然小于n，这时模数n就没有任何作用了，我们直接对c开e次方就能得到明文m代码实现
from Crypto.Util.number import*import gmpy2whileTrue:try: p = getPrime(128) q = getPrime(128) m ='abc' e =3 n = p * q phin =(p -1)*(q -1) d = gmpy2.invert(e, phin)breakexcept:passm = bytes_to_long(m.encode())c =pow(m, e, n)# 破解m = gmpy2.iroot(c, e)[0]print(long_to_bytes(m))
- 低加密指数广播攻击跟上面差不多，e取得太小导致m的e次方仍然小于n
- Coppersmith partial information attack已知p的高位或低位，使用Coppersmith破解出低位达到攻击目的以下是一款数学工具sage的代码
n=113432930155033263769270712825121761080813952100666693606866355917116416984149165507231925180593860836255402950358327422447359200689537217528547623691586008952619063846801829802637448874451228957635707553980210685985215887107300416969549087293746310593988908287181025770739538992559714587375763131132963783147p4=7117286695925472918001071846973900342640107770214858928188419765628151478620236042882657992902#已知P的高位e=65537pbits=512#P原本的位数kbits=pbits - p4.nbits()print(p4.nbits())p4 = p4 << kbitsPR.<x>= PolynomialRing(Zmod(n))f = x + p4roots = f.small_roots(X=2^kbits,beta=0.4)# 经过以上一些函数处理后，n和p已经被转化为10进制if roots: p= p4 +int(roots([0]))print("n",n)print("p",p)print("q",n/p) - wiener attacke过大的时候，可以使用一种基于连分数定理的算法快速破解出d的值。因为e过大的话表现形式就是私钥d会很小github上有开源的攻击代码https://github.com/pablocelayes/rsa-wiener-attack
第三章 数字签名技术
3.1 简介（引用自ctfwiki）
在日常生活中，我们在参加某个活动的时候，可能会需要签名，以便于证明我们确实到场了，，，防止导员啥的，你懂得。。。但其实吧，这种签名很容易被伪造，随便找一个人代签一下，或者说找一个会模仿别人字迹的人帮忙签一下。在计算机世界中，我们可能会需要电子签名，因为我们大多数情况下会使用电子文件，那这时候怎么办呢？当然，我们仍然可以选择使用自己的名字。但其实还有另外一种方式，那就是采用数字签名，这种签名更加难以伪造，可信程度更高。数字签名的主要用处是确保消息确实来自于声称产生该消息的人。
数字签名（digital signature）主要用于对数字消息（digital message）进行签名，以防消息的冒名伪造或篡改，亦可以用于通信双方的身份鉴别。
数字签名依赖于非对称密码，因为我们必须确保一方能够做的事情，而另一方不能够做出这样的事情。其基本原理如下
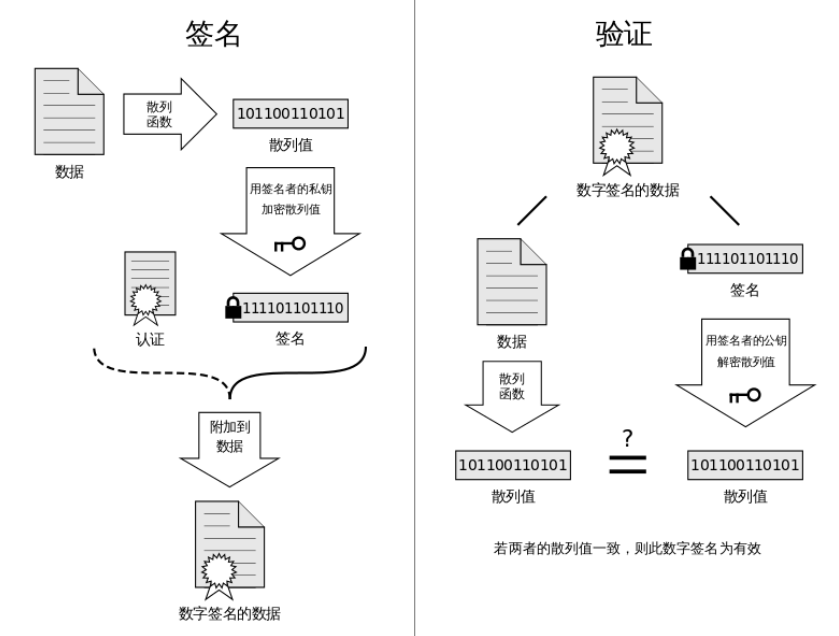
数字签名应当具有以下几个特性：
(1) 签名是可信的：任何人都可以验证签名的有效性。
(2) 签名是不可伪造的：除了合法的签名者之外，任何其他人伪造其签名是困难的。
(3) 签名是不可复制的：对一个消息的签名不能通过复制变为另一个消息的签名。如果对一个消息的签名是从别处复制得到的，则任何人都可以发现消息与签名之间的不一致性，从而可以拒绝签名的消息。
(4) 签名的消息是不可改变的：经签名的消息不能被篡改。一旦签名的消息被篡改，则任何人都可以发现消息与签名之间的不一致性。
(5) 签名是不可抵赖的：签名者事后不能否认自己的签名。
3.2 RSA签名算法
第四章 信息隐藏技术
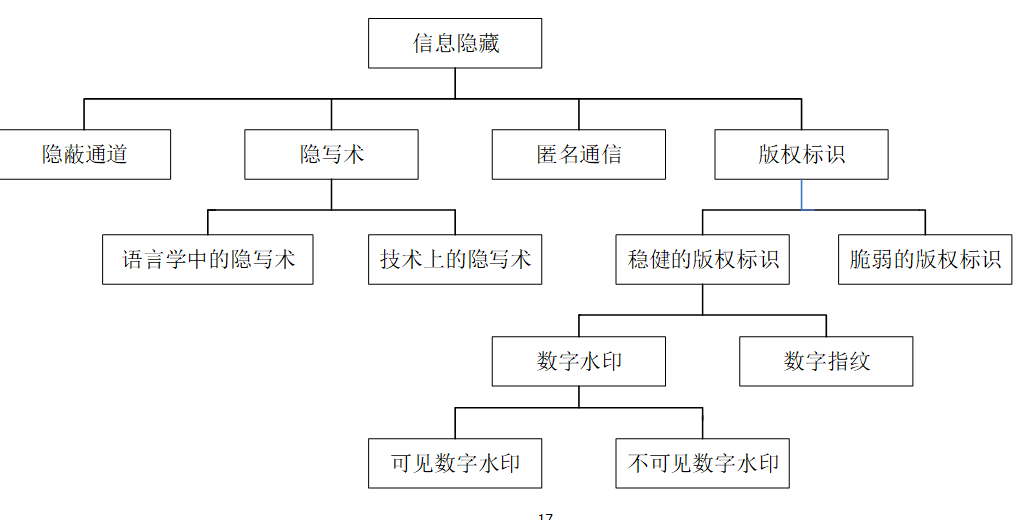
概念
信息隐藏是将秘密信息隐藏在另一非机密的载体信息中，通过公共信道进行传递。攻击者无从判断是否有秘密信息，也无法提取或去除秘密信息。信息隐藏的最大优势在于它并不限制对主信号的存取和访问，而是致力于签字信号的安全保密性
主要应用
- 隐蔽通信
- 数据的完整性
- 图像自恢复
- 版权保护
- 票据防伪
我的猜测
主要可能就是考信息隐藏和信息加密的区别
区别：
目标不同：加密仅仅隐藏了信息的内容；信息隐藏既隐藏了信息内容，还掩盖了信息的存在。
实现方式不同：加密依靠数学运算；而信息隐藏充分运用载体的冗余空间。
应用场合不同：加密只关注加密内容的安全，而信息隐藏还关注载体与隐藏信息的关系。
联系：理论上相互借用，应用上互补。信息先加密，再隐藏。
第五章 应用层安全技术
5.1 web安全技术
概念
Web服务是Internet中最基础的服务之一，不仅被用于搭建信息发布、信息查询、电子商务、电子政务等各种Web网站，而且还被作为文件传输服务、流媒体服务、邮件服务、系统更新服务等网络服务的运行平台。因此，Web服务的安全决定着多种网络服务的安全，也决定着整个Windows系统的安全。
Question
什么是IIS(Internet Information Service)？
IIS即Internet信息服务，是一个用于配置应用程序池或网站、FTP 站点、SMTP或NNTP站点的工具，功能十分强大。利用IIS管理器，管理员可以配置IIS安全、性能和可靠性功能，可添加或删除站点，启动、停止和暂停站点，备份和还原服务器配置，创建虚拟目录以改善内容管理等。（常用的IIS有宝塔Linux，搭过博客的同学可能用过），长这样的
5.2 电子邮件安全
概念
电子邮件就e-mail,这里就不用多说了吧
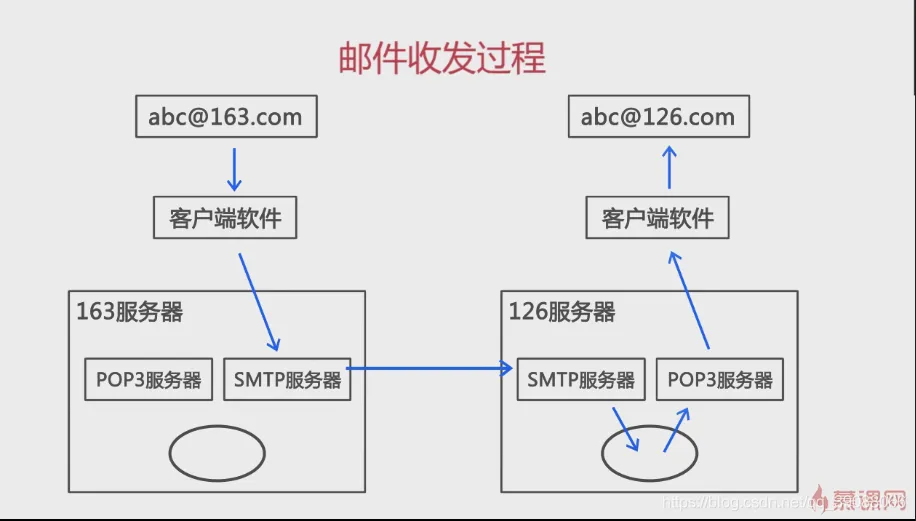
系统组成
- 客户机软件UA（User Agent）：用来处理邮件，如邮件的编写、阅读和管理（删除、排序等）。
- 服务器软件TA（Transfer Agent）：用来传递邮件。
其中，电子邮件不是端到端通信，而是有一个“中间商”负责转发。
收发流程
什么是邮件网关
就是上文说的“中间商”，它能够计算出消息中哪些是重要信息，如主题、发送者、接收者，并把它们翻译成其它系统所需的格式。
除此之外，他还负责负责内部与外部邮件系统的沟通。跟计算机网络中的网关干的事情是一样的。这里以应用层网关为例
例如，一个主机执行的是ISO电子邮件标准，另一个主机执行的是Internet 电子邮件标准，如果这两个主机需要交换电子邮件，那么必须经过一个电子邮件网关进行协议转换，这个电子邮件网关是一个应用网关。
邮件网关主要功能
- 预防功能
- 监控功能
- 跟踪功能
- 账务管理
- 分类统计表
- 邮件备份
按用途划分邮件网关
- 普通邮件网关
- 邮件过滤网关：邮件过滤网关是一个集中检测带毒邮件的独立硬件系统，与用户的邮件系统类型无关，并支持SMTP认证。
- 反垃圾邮件网关：反垃圾邮件网关是基于服务器的邮件过滤和传输系统，可以帮助企业有效管理邮件系统，防止未授权的邮件进入或发出，同时被用于阻挡垃圾邮件、禁止邮件转发和防止电子邮件炸弹。它通过消除不需要的邮件，有效降低网络资源的浪费。
对邮件传输协议的解读
（讲人话版）
- SMTP协议说白了就是你去邮局寄信所需要遵守的规则
- POP3协议就是你去邮局取信所需要遵守的规则
（官方版）
- SMTP协议SMTP（Simple Mail Transfer Protocol）即简单邮件传输协议，它是一组用于由源地址到目的地址传送邮件的规则，用来控制信件的中转方式。SMTP协议属于TCP/IP协议族的应用层协议，它帮助每台计算机在发送或中转信件时找到下一个目的地。通过SMTP协议所指定的服务器，我们就可以把E-mail寄到收信人的服务器上 。SMTP服务器则是遵循SMTP协议的发送邮件服务器，用来发送或中转电子邮件。
- POP3协议POP协议是邮局协议（Post Office Protocol）的缩写，是一种允许用户从邮件服务器收发邮件的协议。POP3（Post Office Protocol 3）即邮局协议的第3个版本，它规定怎样将个人计算机连接到Internet的邮件服务器和下载电子邮件的电子协议，是因特网电子邮件的第一个离线协议标准。POP3允许用户从服务器上把邮件存储到本地主机，同时删除保存在邮件服务器上的邮件。POP3服务器则是遵循POP3协议的接收邮件服务器，用来接收电子邮件的。与SMTP协议相结合，POP3是目前最常用的电子邮件服务协议。
什么是垃圾邮件
大家都收到过垃圾邮件吧，这里就不多说了
- 匿名转发（没有发件人信息）
- 电子邮件欺骗（换了层马甲）
- E-mail炸弹（相当于短信轰炸那种效果）
反垃圾邮件技术
- 过滤技术（1）关键词过滤（2）黑白名单（3）HASH技术（4）基于规则过滤（5）智能和概率系统
- 验证查询
- 挑战
- 密码术（1）目前电子邮件在传输中使用的是SMTP协议，它不提供加密服务，攻击者可在邮件传输中截获数据。（2）两种端到端的安全技术：PGP（Pretty Good Privacy）和S/MIME（Secure Multi-Part Intermail Mail Extension）。（3）主要功能就是身份的认证和传输数据的加密。
PGP技术
我们做实验用过的，就是把发送的信息经过加密再发出去，让攻击者不能轻易破解我们的数据，保证信息的安全，它的加密算法包括多个方面。
概念
PGP是一个基于公开密钥加密算法的应用程序，该程序创造性在于把RSA公钥体系的方便和传统加密体系的高速度结合起来，并在数字签名和密钥认证管理机制上有巧妙的设计。
特点
- 加密速度快
- 可移植性出色
- 源代码是免费的
5.3 数据库安全
数据库安全面临的最大威胁就是sql注入了，也是整个网络安全体系里危害最大，影响范围最大的漏洞。
浅析sql注入
question
- 什么是sql注入？sql注入说白了就是后端程序员在写sql语句的时候没有对用户的输入进行限制导致用户可以构造一些sql语句然后被带到数据库里联合查询，暴露出数据库的信息，严重的还会导致被删库，修改数据库的信息等等。我们这里以sqli-lab上的一道题为例，看看sql注入到底是怎样实现的。这是那道题源码的核心部分
$sql="SELECT * FROM users WHERE id='$id' LIMIT 0,1";$result=mysql_query($sql);$row=mysql_fetch_array($result);虽然是用php写的，但是我们来看这句sql$sql="SELECT * FROM users WHERE id='$id' LIMIT 0,1";按理来说，这里的逻辑是你输入一个id，然后后端去数据库里查这个id对应的用户信息对吧？前端页面长这样
我们来试试id=1会查出什么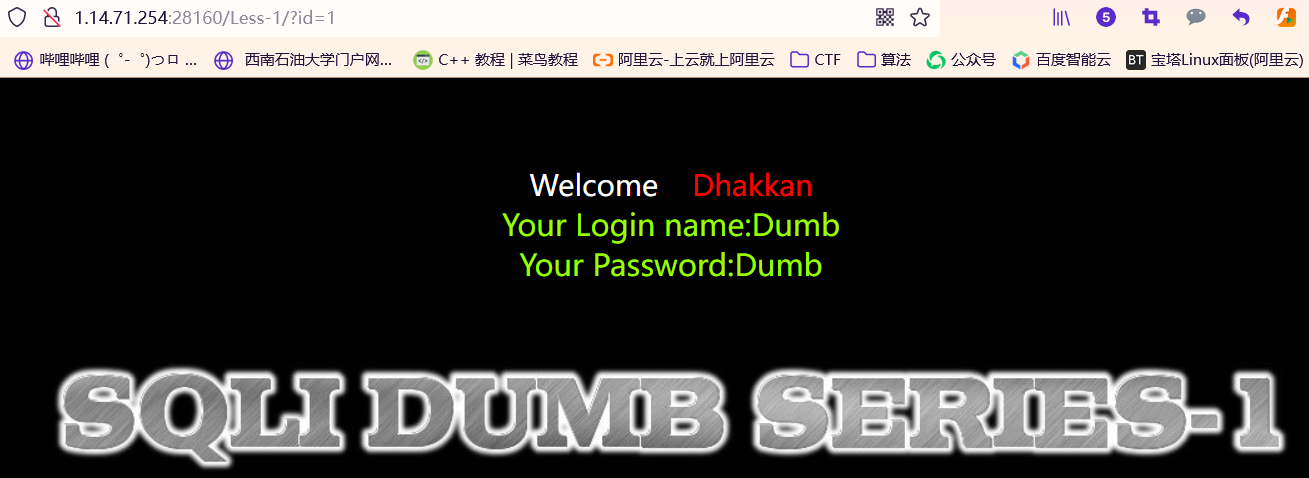
没有任何问题对吧，我们来尝试SQL注入一下http://1.14.71.254:28160/Less-1/?id=1'注意，我们在1后面多写了一个’，那么现在的sql语句变成啥样了呢？$id="1'";$sql="SELECT * FROM users WHERE id='1' ' LIMIT 0,1";看sql语句里id那个地方，我们的单引号把前面的单引号闭合掉了，如果我们再加一个#注释掉后面的话，sql语句就变成了这样$sql="SELECT * FROM users WHERE id='1'";这里看起来还很正常对吧，那如果我们加一句联合查询呢?$id="1' union select * from users #";//实际上我们并不知道数据库里实际的表名，这里仅作演示sql语句就会变成这样$sql="SELECT * FROM users WHERE id='1' union select * from users";这句联合查询是不是就会把user表的所有信息返回出来？sql注入的目的就达成了。考试考不到这么难，这里只是让同学们看看实际的sql注入流程到底是什么样的。 - 怎样防范sql注入？前面我们看到了sql注入的成因就是没有对用户的输入作限制，所以防范的方法也很简单，限制用户的输入呗。- 对文本框进行过滤（用户输入），将SQL中使用的特殊符号，如“’”，“-”，“%”,”;”等，用Replace()方法过滤掉。- 限制文本框输入字符长度- 检查用户输入的合法性- 使用带参数的SQL语句形式：确保从外部源接收的值仅作为值来传递，而不作为SQL的一部分传递。- 保持异常信息的私有性。
第六章 计算机病毒及防范
6.1 计算机病毒概述
定义
和生物病毒差不多，具有破坏性，并且复制、转播能力极强，本质是一个程序，一段可执行码。
特点
- 不能作为独立的可执行程序运行
- 自我复制
- 通过执行宿主程序来激活病毒
- 跨平台
分类（按功能划分）
- 感染型病毒 ：危害最大
- 蠕虫病毒：传播载体多，传播能力强
- 后门程序：远程操控
- 木马病毒：隐藏、窃取
- 病毒工具：网络媒介
- 病毒生成器：拼积木形式
- 搞笑程序：愚弄
危害
这个不用多说大家都懂病毒的危害性
6.2 VBS病毒
概念
基于VBScript这门编程语言编写，通过调用一些公开的Windows对象，组件，可以直接对文件系统，注册表等进行控制。
特点
1．编写简单，一个以前对病毒一无所知的病毒爱好者可以在很短的时间里编出一个新型病毒来。
2．破坏力大。其破坏力不仅表现在对用户系统文件及性能的破坏。他还可以使邮件服务器崩溃，网络发生严重阻塞。
3．感染力强。由于脚本是直接解释执行，并且它不需要像PE病毒那样，需要做复杂的PE文件格式处理，因此这类病毒可以直接通过自我复制的方式感染其他同类文件，并且自我的异常处理变得非常容易。
4．传播范围大。这类病毒通过htm文档，Email附件或其它方式，可以在很短时间内传遍世界各地。
5．病毒源码容易被获取，变种多。由于VBS病毒解释执行，其源代码可读性非常强，即使病毒源码经过加密处理后，其源代码的获取还是比较简单。因此，这类病毒变种比较多，稍微改变一下病毒的结构，或者修改一下特征值，很多杀毒软件可能就无能为力。
6．欺骗性强。脚本病毒为了得到运行机会，往往会采用各种让用户不大注意的手段，譬如，邮件的附件名采用双后缀，如.jpg.vbs，由于系统默认不显示后缀，这样，用户看到这个文件的时候，就会认为它是一个jpg图片文件。
7．使得病毒生产机实现起来非常容易。所谓病毒生产机，就是可以按照用户的意愿，生产病毒的机器（当然，这里指的是程序），目前的病毒生产机，之所以大多数都为脚本病毒生产机，其中最重要的一点还是因为脚本是解释执行的，实现起来非常容易，具体将在我们后面谈及。
原理
- 首先将计算机病毒自身代码赋给字符串变量VBscopy。
- 将这个字符串覆盖到目标文件并创建一个以目标文件名为文件名前缀，以vbs为扩展名的文件副本，最后删除目标文件。
- 通过scan（）函数主要寻找满足条件的文件，并生成对应文件的计算机病毒副本
- 通过递归的方法遍历整个目录和文件。
6.3 蠕虫病毒
概念
蠕虫病毒是一种常见的计算机病毒，是无须计算机使用者干预即可运行的独立程序，它通过不停的获得网络中存在漏洞的计算机上的部分或全部控制权来进行传播。计算机病毒是指编制或者在计算机程序中插入的破坏计算机功能或者破坏数据．影响计算机使用并且能够自我复制的一组计算机指令或者程序代码。（熊猫烧香就是经典的蠕虫病毒）
特点
- 独立性较强
- 寻找系统漏洞实施主动攻击
- 传播范围更广，传播速度更快
- 采用高明的方法进行伪装和隐藏
- 使用先进的技术
6.4 木马
概念
木马全称为特洛伊木马，来源于古希腊神话。木马是通过欺骗或诱骗的方式安装，并在用户的计算机中隐藏以实现控制用户计算机的目的。是具有远程控制、信息窃取、破坏等功能的恶意代码
特点
- 欺骗性 木马都有很强的欺骗性，执行通常都由被攻击者自己执行起来的
- 隐藏性
- 非授权性 执行恶意操作是没有经过用户授权的
- 交互性 主机之外的攻击者可以通过某种方式对主机进行交互
经典例子：php一句话木马，感兴趣的同学可以去试试
<?php @eval($_GET["cmd"]);?>
6.5 计算机病毒防范
常用方法
- 安装杀毒软件
- 不要浏览不正规的网站
- 培养自觉的信息安全意识
- 用Windows Update功能打全系统补丁
第七章 防火墙
7.1 防火墙概述
概念
- “防火墙”，是指一种将内部网和公众访问网（如Internet）分开的方法，它实际上是一种隔离技术。
- 防火墙是在两个网络进行通信时执行的一种访问控制尺度，它被用来保护计算机网络免受非授权人员的骚扰，防止黑客的入侵。
基本属性
- 防火墙是不同网络或网络安全域之间信息流通过的唯一出入口，所有双向数据流必须经过它。
- 只有被授权的合法数据，即防火墙系统中安全策略允许的数据，才可以通过。
- 逻辑上，防火墙是一个分离器、一个限制器，也是一个分析器，他有效地监控了内网和Internet之间的所有活动，保证内网安全。
7.2 防火墙的功能
- 网络安全屏障
- 强化网络安全策略基于以下四种技术1. 服务控制——确定可以访问的网络服务类型。防火墙可以在IP地址和TCP端口号的基础上过滤通信量。2. 方向控制——确定特定的服务请求通过防火墙流动的方向。3. 用户控制——根据哪个用户尝试访问服务来控制对于一个服务的访问。4. 行为控制——控制怎样使用特定的服务。
- 对网络存取和访问进行监控审计
- 防止内部信息外泄
- 保护内网安全
7.3 防火墙的局限性
- 防火墙会限制有用的网络服务。
- 防火墙无法防护内部网络用户的攻击。
- 防火墙无法防范通过防火墙以外的其他途径的攻击。
- 防火墙不能防止传送已感染病毒的软件或文件。
- 防火墙无法防范数据驱动型的攻击。
- 防火墙不能防备新的网络安全问题。
因为防火墙本质上就是一个病毒库，他只能对比你的计算机里面有没有他库里面的病毒，而且他是一种被动防御，所以不会主动去发现新的计算机病毒。
7.4 防火墙基本原理
- 所有防火墙功能的实现都依赖于对通过防火墙的数据包的相关信息进行检查，而且检查的项目越多、层次越深，则防火墙越安全。
- 对于一个防火墙来说，如果知道了其运行在OSI参考模型的哪一层，就可以知道它的体系结构是什么，主要的功能是什么。
就是对计算机网络中每一层的数据包进行检查，检查的层数越多防火墙越安全。
7.5 分布式防火墙
概念
- 分布式防火墙是一种主机驻留式的安全系统，用于保护企业网络中的关键节点服务器、数据及工作站免受非法入侵的破坏。
- 内核模式
- 所有信息进行过滤和限制既能阻止非法入侵，也能入侵检测及防护功能
结构
- 主要以软件形式
- “三层”过滤检查
- 中央策略管理服务器统一负责设置安全策略
- 与传统防火墙的边界不同
- 分布式防火墙是一个完整的系统，而不是一个单一产品，根据功能可以划分为如下几个部分：网络防火墙，主机防火墙，中心管理软件。
特点
- 主机驻留
- 嵌入操作系统（前置机）
- 类似于个人防火墙
7.6 不同类型防火墙优缺点对比
传统防火墙不足
- 结构性限制：内外网的概念不好区分。
- 防外不防内：功能有限。
- 效率问题：容易形成网络瓶颈。
- 故障问题：单点故障
分布式防火墙优势
- 适用于服务器托管（大数据中心）
- 增强了系统安全性（入侵检测）
- 消除了结构性瓶颈问题，提高了系统性能（单一的接入点）
- 随系统扩充（分布式特性）
- 应用更为广泛且支持VPN通信
第八章 入侵检测系统
8.1 入侵检测系统简介
入侵检测基本概念
入侵检测则是对入侵行为的发觉。它通过对计算机网络或计算机系统中的若干关键点收集信息并对其进行分析，从而发现网络或系统中是否有违反安全策略的行为和被攻击的迹象。和防火墙是不同的。
入侵检测系统（IDS）基本概念
入侵检测系统(Intrusion Detection System,IDS) 它是探测计算机网络攻击行为的软件或硬件。作为防火墙的合理补充，它可以帮助网络管理员探查进入网络的入侵行为，从而扩展系统管理员的安全管理能力。
IDS主要功能
- 监测并分析用户和系统的活动
- 核查系统配置和漏洞
- 评估系统关键资源和数据文件的完整性
- 识别已知的攻击行为
- 统计分析异常行为
- 操作系统日志管理，并识别违反安全策略的用户活动
为什么有了防火墙还需要IDS
- 防火墙策略满足不了高安全的要求
- 作用互补：“守卫”与“巡警”
IDS的通用模型CIDF
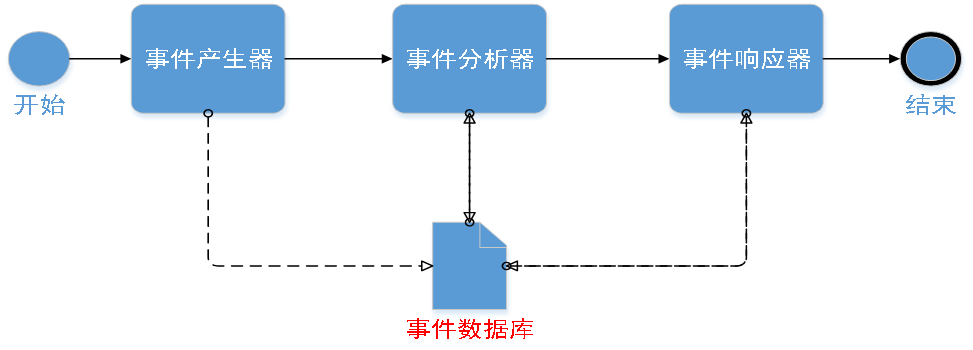
主要模块：
- 事件产生器（Event Generators）
- 事件分析器（Event Analyzers）
- 响应单元（Response Units）
- 事件数据库（Event Databases）
职责分类
- 信息收集位置：在计算机网络系统中的若干不同关键点（不同网段和不同主机）收集信息。（1）扩大检测范围（2）“一致性”检测 内容：包括系统、网络、数据及用户活动的状态和行为 质量：信息正确性和可靠性入侵检测信息来源系统和网络日志文件：利用系统和网络日志文件信息是入侵检测的必要条件。目录和文件中不期望的改变：正常情况下的限制访问或修改系统日志文件。程序执行中的不期望行为物理形式的入侵信息（1）对网络硬件的未授权连接（2）对物理资源的为授权访问
- IDS信号分析手段- 模式匹配：将收集到的信息和已知的网络入侵和系统误用模式数据库进行比对。 1. 优点：准确、效率高2. 缺点：需要不断更新，无法检测未出现过的攻击- 统计分析：首先给系统对象创建一个统计描述，统计正常使用时的一些测量属性。任何观测值在正常范围之外的，就认为有入侵行为发生。 1. 优点：可检测到未知和更为复杂的入侵2. 缺点：误报、漏报率高- 完整性分析：完整性分析主要关注某个文件或对象是否被更改，通常采用强有力的加密机制（如Hash函数）来识别微小变化。 1. 优点：能发现攻击导致文件或对象发生的任何改变2. 缺点：无法实时响应，只能事后分析
- IDS常见的响应处理- 警告和事件报告。- 终止进程，强制用户退出。- 切断网络连接，修改防火墙设置。- 灾难评估，自动恢复。- 查找定位攻击者。
8.2 IDS分类
根据监测位置（数据来源）进行分类：
- 基于网络的IDS基于网络的IDS对数据包进行分析以探测针对网络的攻击，这种IDS嗅探网络数据包，并将数据流与已知入侵行为的特征进行比较。- 优点：（1）全网监控（2）满足各种性能需求- 缺点：（1）带宽要求：流量<探测器的处理能力（2）无法处理加密数据
- 基于主机的IDS过在主机或操作系统上检查有关信息来探测入侵行为，这种IDS通过系统调用，审计日志和错误信息等对主机进行分析。- 优点：（1）确定一个攻击是否成功。（2）利用主机自己的IP协议栈来防御对数据包分片重组、改变生存时间等基于网络的IDS是比较难处理这类攻击的 。- 缺点：（1）网络监控的范围有限：不能监测针对主机的端口扫描（2）挑战：必须运行在网络的中所有操作系统上
根据入侵检测技术分类：
- 特征检测对于基于特征的检测技术来说，首先要定义违背安全策略的事件的特征，如网络数据包的某些头信息。检测主要判别这类特征是否在所收集到的数据中出现。
- 异常检测基于异常的检测技术则是先定义一组系统“正常”情况的数值，然后将系统运行时的数值与所定义的“正常”情况比较，得出是否有被攻击的迹象。这种检测方式的核心在于如何定义所谓的“正常”情况。（跟你去医院查血常规差不多）
这两种检测技术的比较
- 结论有非常大的差异
- 基于特征的检测技术的核心是维护一个知识库，对于已知的攻击，它可以详细、准确地报告出攻击类型，但是对未知攻击的检测能力都很有限，而且知识库必须不断更新。
- 基于异常的检测技术则无法准确判别出攻击的手段，但它可以判别更广范、甚至未发觉的攻击。
根据检测原理分类：
- 异常检测：基于模型的检测 1. 从模型类型上来分类：基于规则（先验经验）–>基于统计抽样–>基于人工神经网络2. 从实现方式上来分类：自学习系统和编程系统
- 规则库检测：特征检测
- 混合检测 1. （明确）分析系统的正常行为2. （可疑）观察可疑的入侵行为3. 判断更全面、准确、可靠
8.3 IDS面临的挑战
- 提高IDS的检测速度，以适应网络通信的要求
- 减少IDS的漏报和误报，提高其安全性和准确度
- 提高IDS的互动性能，从而提高整个系统的安全性能。
第九章 网络安全协议
9.1 安全协议概述
安全协议（Security protocol，又称密码协议，Cryptographic protocol）。安全协议是建立在密码体制基础上的一种交互通信协议，它运用密码算法和协议逻辑来实现认证和密钥分配等目标。产生原因是早期的一些协议没有对数据进行加密导致的一系列安全问题。
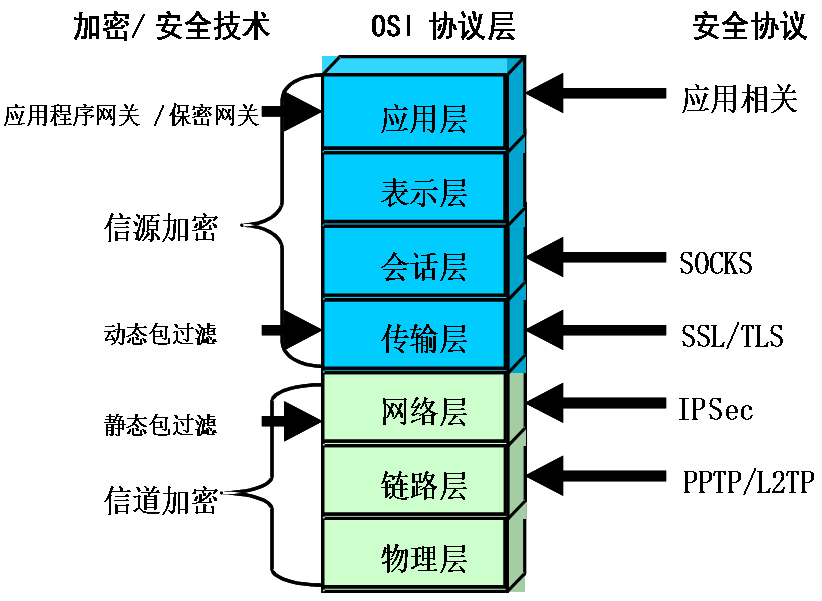
9.2 常见的网络安全体系结构
TCP/IP的安全体系结构
IPSec协议族的体系结构
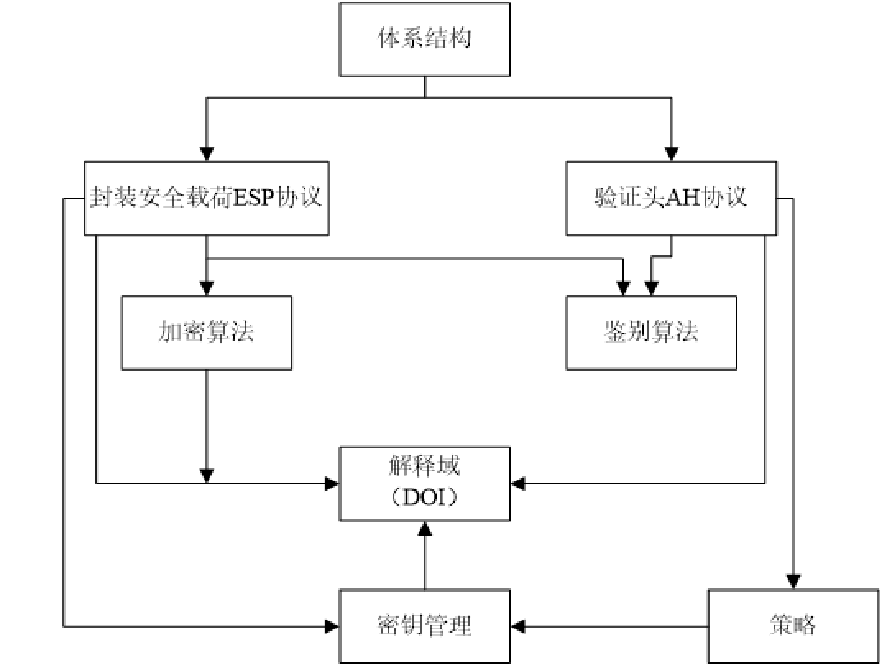
AH（认证头）协议
IPsec 认证头协议（IPsec AH）是 IPsec 体系结构中的一种主要协议，它为 IP 数据报提供无连接完整性与数据源认证，并提供保护以避免重播情况。一旦建立安全连接，接收方就可能会选择后一种服务。 AH 尽可能为 IP 头和上层协议数据提供足够多的认证。
ESP（载荷封装）协议
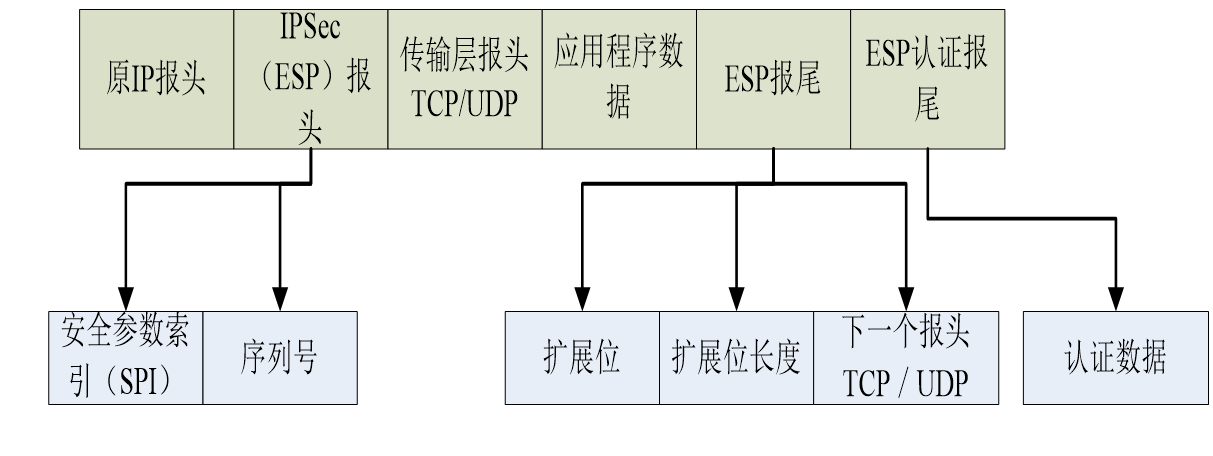
ESP协议数据单元格式三个部分组成，除了头部、加密数据部分外，在实施认证时还包含一个可选尾部。
第十章 VPN技术
10.1 常用的远程连接方法
- 利用拨号技术来实现远程连接（数字/模拟）
- 利用VPN实现远程连接1. 硬件：路由器VPN2. 软件：常用个人远程协助软件（花生壳，向日葵，Teamviewer）
- 无线远程连接
10.2 VPN概念
- “虚拟” （Virtual）指的是一种逻辑连接，“专用或私有”（Private）指的是排他性的连接，“网络”（Network）指按某种协议进行通信的计算机集合。
- 实现不同网络间组件和资源的相互连接
- 提供与专用网络一样的安全与功能保障
- 远程连接方法之一
VPN基本要求
- 用户验证
- 地址管理
- 数据加密
- 密钥管理
- 多协议支持
特点
- 采用加密、认证和隧道技术，利用公共通信网络设施的一部分来发送专用网络信息。
- 为相互通信的节点建立一个相对封闭的、逻辑上的专用网络。
- 只允许特定的利益集团内（VPN内部）建立对等连接，保证在网络中传输的数据的保密性。
- 能灵活利用多种公用远程通信网络来实现不同内部局域网之间、网络与主机之间的远程信息交换。
优点
- 节省成本
- 实现网络安全
- 简化网络结构
- 连接的随意性
- 掌握自主权
10.3 隧道技术
定义
隧道技术是一种通过使用互联网络的基础设施在网络之间传递数据的技术。注意隧道技术是指包括数据封装，传输和解包在内的全过程。
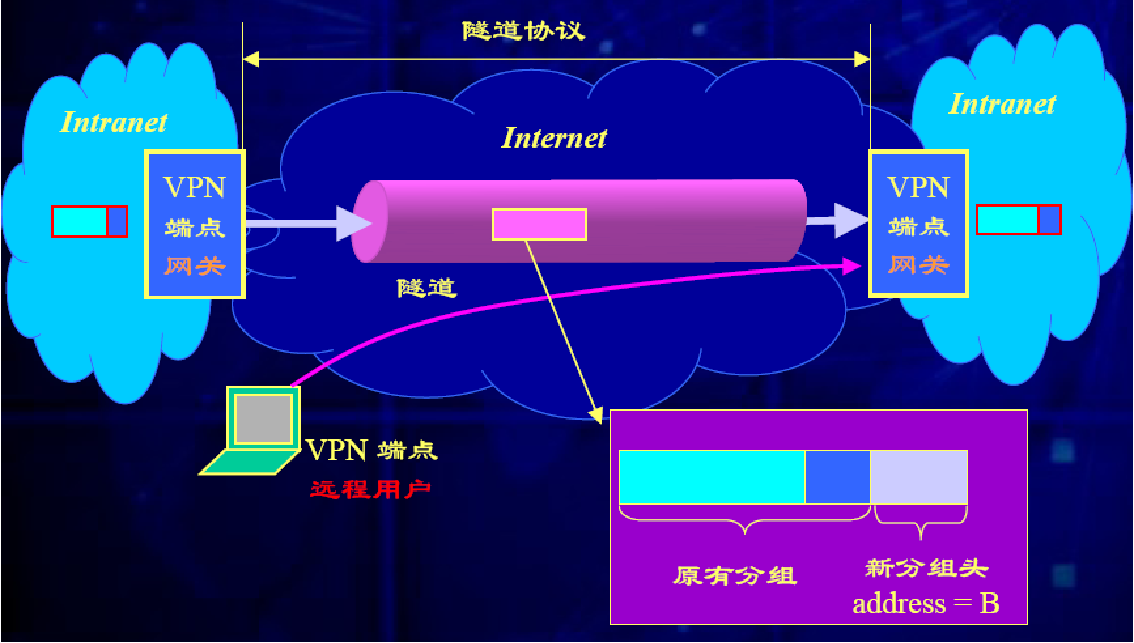
隧道基本要求：
- 用户验证
- 令牌卡（Tokencard)支持
- 动态地址分配
- 数据压缩
- 数据加密
- 密钥管理
- 多协议支持
第十一章 无线网络及安全评估
11.1 无线网络概述
概念
WLAN是指以无线信道作传输媒介的计算机局域网，是有线联网方式的重要补充和延伸，并逐渐成为计算机网络中一个至关重要的组成部分，广泛适用于需要可移动数据处理或无法进行物理传输介质布线的领域。目前最为热门的三大无线技术是WiFi、蓝牙以及HomeRF
工作模式
- 点对点（AD-hoc）模式点对点模式（ 或Peer-to-Peer）是最简单的无线网络连接方式，这种模式允许两台或多台计算机不依赖于任何控制中心就能够相互通信。搭建一个AD-hoc模式的无线网络非常简单，硬件的需求最少，只需每台计算机具有都支持同一种协议（如IEEE 802.11）的无线网卡即可。
- Infrastructure构建一个无线热点最好采用Infrastructure方式，它不需要让某一台计算机一直开着，同时也提供了一定的安全机制。
11.2 无线网络协议
- WEP协议WEP(Wired Equivalent Privacy)协议是IEEE802.11b协议中最基本的无线安全加密措施，其主要用途包括提供接入控制，防止未授权用户访问网络；对数据进行加密，防止数据被攻击者窃听；防止数据被攻击者中途恶意纂改或伪造。此外，WEP也提供认证功能。
- IEEE 802.11i安全标准这种安全标准为了增强WLAN的数据加密和认证性能，定义了RSN(Robust Security Network)的概念，并且针对WEP加密机制的各种缺陷做了多方面的改进。（比WEP牛逼一些）
- WAPI协议WAPI安全机制由 WAI(WLAN Authentication Infrastructure)和WPI(WLAN Privacy Infrastruc-ture)两部分组成，WAI和WPI分别实现对用户身份的鉴别和对传输的数据加密。WAPI能为用户的WLAN系统提供全面的安全保护。WAPI安全机制包括两个组成部分。
11.3增强安全的措施
- 采用强力的密码。
- 严禁广播服务集合标识符(SSID)。
- 采用有效的无线加密方式。
- 可能的话，采用不同类型的加密。
- 对介质访问控制(MAC)地址进行控制。
- 关闭无线网络接口。
- 对网络入侵者进行监控。
- 确保核心的安全。
11.4 信息安全评估
11.4.1 国内外评价标准
网络安全标准是保障网络安全技术和产品,在设计、研发、建设、实施、使用、测评和管理维护过程中,解决一致性、可靠性、可控性、先进性和符合性的技术规范和依据.也是政府宏观管理重要手段,信息安全保障体系重要组成部分。
国外评价标准
- 美国TCSEC(橙皮书)
- 美国联邦准则(FC)
- 欧洲ITSEC(白皮书)
- 通用评估准则(CC)
- ISO 安全体系结构标准
国内评价标准
系统安全保护等级划分准则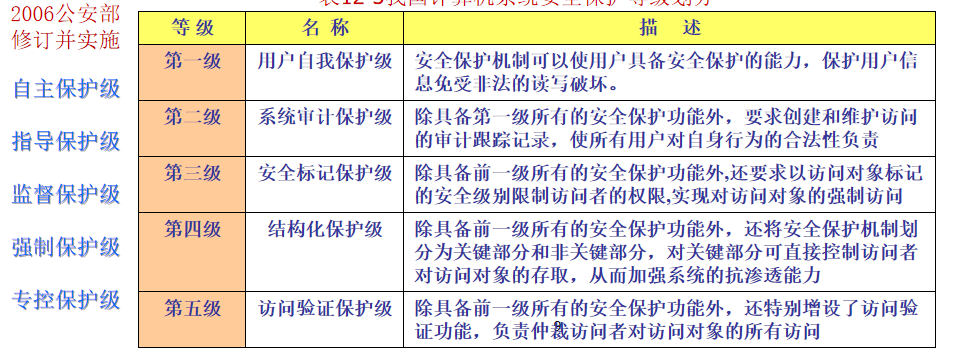
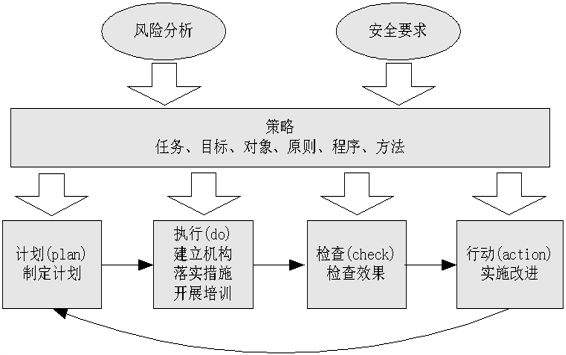
11.4.2 网络安全管理过程PDCA
11.4.3 网络信息安全风险评估
定义
从风险管理角度，运用科学的方法和手段，系统地分析网络与信息系统所面临的威胁及其存在的脆弱性，评估安全事件一旦发生可能造成的危害程度，提出有针对性的抵御威胁的防护对策和整改措施。
风险评估的意义
- 明确企业信息系统的安全现状企业准确地了解自身的网络、各种应用系统以及管理制度规范的安全现状，从而明晰企业的安全需求
- 确定企业信息系统的主要安全风险可以确定企业信息系统的主要安全风险，并让企业选择避免、降低、接受等风险处置措施。
- 指导企业信息系统安全技术体系与管理体系的建设
风险评估实施步骤
- 风险评估的准备
- 资产识别
- 威胁识别
- 脆弱性识别
- 已有安全措施的确认
- 风险分析
- 风险评估文件记录
11.5 相关法律法规
中国从网络安全整治管理的需要出发，国家及相关部门、行业和地方政府相继制定了多项有关网络安全的法律法规。中国网络安全立法体系分为以下三个层面：
- 第一层面：法律。是全国人民代表大会及其常委会通过的法律规范。我国同网络安全相关的法律有：《立法法》、《宪法》、《刑法》、《治安管理处罚条例》、《刑事诉讼法》、《国家安全法》、《保守国家秘密法》、《行政处罚法》、《行政诉讼法》、《关于维护互联网安全的决定》、《网络安全法》、《行政复议法》、《国家赔偿法》等。
- 第二个层面：行政法规。主要是国务院为执行宪法和法律而制定的法律规范。与网络信息安全有关的行政法规包括《计算机信息系统安全保护条例》、《计算机信息网络国际联网管理暂行规定》、《计算机信息网络国际联网安全保护管理办法》、《商用密码管理条例》、《中华人民共和国电信条例》、《互联网信息服务管理办法》、《计算机软件保护条例》等。
- 第三个层面：地方性法规、规章、规范性文件。主要是国务院各部、委根据法律和国务院行政法规与法律规范，以及省、自治区、直辖市和较大的市人民政府根据法律、行政法规及其法律规范性文件。公安部制定的《计算机信息系统安全专用产品检测和销售许可证管理办法》、《计算机病毒防治管理办法》、《金融机构计算机信息系统安全保护工作暂行规定》和有关计算机安全员培训要求等。工业和信息化部制定的《互联网电户公告服务管理规定》、《软件产品管理办法》、《计算机信息系统集成资质管理办法》、《国际通信出入口局管理办法》、《国际通信设施建设管理规定》、《中国互联网络域名管理办法》、《电信网间互联管理暂行规定》等。
版权归原作者 bestkasscn 所有， 如有侵权，请联系我们删除。