**1. 数学建模介绍 **
1.1 数学建模概念
数学建模是将实际问题转化为数学问题,通过建立数学模型、编写程序求解的过程,如某区域水资源评价问题、水利工程项目风险评价问题、水资源污染增长预测问题、快递员派送快递的最短路径问题等等。1.2 数学模型的概念
数学模型是运用数理逻辑方法和数学语言建构的科学或工程模型,通俗的讲就是数学方法,例如初中就学过的线性规划模型,高中学过的方差分析模型、排队论、图论,大学学过的插值拟合模型、常微分方程模型等等。这些都是学过的,还有些没有学过的主要有:层次分析法、神经网络模型、模糊数学模型、灰色系统理论模型、遗传算法模型、模拟退火算法模型。1.3 数学建模模型的分类及其应用
数学建模模型主要分为三大类:预测模型、优化模型、评价模型。 预测模型:神经网络预测、灰色预测、拟合插值预测(线性回归)、时间序列预测、马尔科夫链预测、微分方程预测、Logistic模型等等。应用领域:人口预测、水资源污染增长预测、病毒蔓延预测、竞赛获胜概率预测、月收入预测、销量预测、经济发展情况预测等在工业、农业、商业等经济领域,以及环境、社会和军事等领域中都有广泛的应用。
优化模型:规划模型(目标规划、线性规划、非线性规划、整数规划、动态规划)、图论模型、排队论模型、神经网络模型、现代优化算法(遗传算法、模拟退火算法、蚁群算法、禁忌搜索算法)等等。 应用领域:快递员派送快递的最短路径问题、水资源调度优化问题、高速路口收费站问题、军事行动避空侦察的时机和路线选择、物流选址问题、商区布局规划等各个领域。 评价模型:模糊综合评价法、层次分析法、聚类分析法、主成分分析评价法、灰色综合评价法、人工神经网络评价法等等。 应用领域:某区域水资源评价、水利工程项目风险评价、城市发展程度评价、足球教练评价、篮球队评价、水生态评价、大坝安全评价、边坡稳定性评价等领域。1.4 数学建模发展介绍
最早起源于美国,即美国大学生数学建模竞赛(1985年),美赛是数学建模的鼻祖,初始只有几十支队伍参赛,后来清华大学、北京大学、复旦大学等也参加了美国赛,后来由清华大学姜启源等教授把数学建模逐渐引入国内,1992年开始举办中国大学生数学建模竞赛,1999年美国大学生数学建模竞赛有了跨学科的数学建模竞赛(与经济学、政治学、化学、生物学等学科交叉),1999年美国又开始举办了中学生数学建模竞赛,2004年中国开始举办全国研究生数学建模竞赛,2014年中国开始举办全国中学生数学建模竞赛。1.5 竞赛流程介绍
大学生和研究生数学建模竞赛每年4月份开始下达竞赛通知,6月份开始报名,9月中旬开始竞赛,11月份公布结果、12月份举行颁奖典礼,12月末发放获奖证书。 大学生竞赛时间为三天三夜(72小时),研究生竞赛时间为四天四夜零四小时(100小时),三名学生一队,写一篇大约30页左右的数学建模赛题解决方案论文,主要内容包括:摘要、关键词、问题重述(背景+赛题介绍)、问题分析、符号说明、模型建立与求解(核心部分)、模型评价及优缺点、模型推广、参考文献、附录(数据表、图、程序代码)、附件(论文的PDF版和WORD版、画图源程序、求解源程序、EXCEL数据处理表等等)。1.6 参加数学建模的好处
数学建模竞赛的奖项不仅仅对你考研的复试或就业面试有一定的帮助,更重要的是你在学习数学建模期间可以很好锻炼自己的科研能力。可以说一次参赛,受益终身!以下是我罗列的好处,仅供参考:(1)评奖评优加分,在某些学校评国家奖学金和学业奖学金。
(2)参加就业面试、升学面试有优势,国家级奖项。
(3)一些地方落户加分,如上海落户加分,国家一等奖加10分,国家二等奖加8分,国家三等奖加6分。
(4)对学术科研有较大帮助,①在论文排版上有较大提高;②在数据处理能力上也有较大提高;③在数学计算、数据处理、画图软件的使用有较大的提高;④所学的数学模型能够更好的应用到发表的学术论文和硕士学位论文中,如层次分析法、模糊综合评价法等常用到工程项目评价中,遗传算法、蚁群算法等常用到水库调度、大坝裂缝监测等方面,神经网络、灰色理论等常用到人口预测预报等方面。
(5)打开我们的生活与数学之间的桥梁,而且还能学习很多非常有用的数学知识,也能锻炼逻辑思维能力。
2. 建模比赛类型及网站
2.1 全国大学生数学建模竞赛
官网网站:全国大学生数学建模竞赛
历年赛题原文网址:全国大学生数学建模竞赛
历年获奖名单:全国大学生数学建模竞赛
2.2 美国大学生数学建模竞赛
官网网站:COMAP: Mathematics Instructional Resources for Innovative Educators
历年赛题原文网址:MCM: The Mathematical Contest in Modeling
历年获奖名单:MCM: The Mathematical Contest in Modeling
2.3 中国研究生数学建模竞赛
历年赛题原文网址:http://gmcm.seu.edu.cn/31/list.htm
**3. 数学建模常用软件 **
数学建模与软件应用之间的关系是密不可分的,数学建模主要就是用数据说话,需要用软件对数据进行处理和计算,数学建模中最常用的软件是MATLAB软件。下面加粗为重点掌握。
- 优化计算:MATLAB、LINGO/LINDO、Mathematica
- 数据处理:EXCEL、ORIGIN、SPSS
- 统计分析:SAS、SPSS、stata、eviews
- 画图软件:MATLAB、EXCEL、WORD、ORIGIN、AUTO CAD、VISIO、Photoshop(图片修理)
- 论文排版:word、latax(美赛常用)
- 查看文献:CAJ阅览器、PDF****阅读器
** 4. 论文写作要求**
赛题:不仅要写题号,还要想一个符合本文的题目,也可以为原赛题题目。
摘要:摘要的好坏也是决定论文的成败;摘要分三部分,导语,每一题介绍、结语,重点在每题介绍,格式为:a. 模型的数学归类(在数学上属于什么类型);b. 建模的思想(思路);c. 算法思想(求解思路);d. 建模特点(模型优点,建模思想或方法,算法特点,结果检验,灵敏度分析,模型检验……);e. 主要结果(数值结果,结论;回答题目所问的全部“问题”)。注意表述:准确、简明、条理清晰、合乎语法、字体工整漂亮;打印最好,但要求符合文章格式。务必认真校对。
关键词:3-5个关键词、突出主题、突出优势。问题重述:包括问题背景和问题 解释,不能完全抄原题,也不要完全自己写,在原题的基础上进行简化、调整。
问题分析:先进性整体思路分析,可以有本文的思路框架图,然后对每一小问分别分析。
模型假设:把题目中提出的忽略的部分写进去,自己模型中局限性的条件写进去等等,关键性假设不能缺;假设要切合题意。。
符号说明:主要是模型建立中公式中的符号,在这里集中列表说明,后面模型中也要有;有时也可以进行名词解释。
模型建立与求解:此部分是论文的核心,图表不能大量罗列,多的部分可放到附录中或附件中。
模型建立:
a. 基本模型:
ⅰ)首先要有数学模型:数学公式、方案等;
ⅱ)基本模型,要求 完整,正确,简明;
b. 简化模型:
ⅰ)要明确说明简化思想,依据等;
ⅱ)简化后模型,尽可能完整给出;
c. 模型要实用,有效,以解决问题有效为原则。
数学建模面临的、要解决的是实际问题,不追求数学上的高(级)、深(刻)、难(度大)。
ⅰ )能用初等方法解决的、就不用高级方法;
ⅱ)能用简单方法解决的,就不用复杂方法;
ⅲ)能用被更多人看懂、理解的方法,就不用只能少数人看懂、理解的方法。
d.鼓励创新,但要切实,不要离题搞标新立异。数模创新可出现在:
▲ 建模中,模型本身,简化的好方法、好策略等;
▲ 模型求解中;
▲ 结果表示、分析、检验,模型检验;
▲ 推广部分。
e.在问题分析推导过程中,需要注意的问题:
ⅰ)分析:中肯、确切;
ⅱ)术语:专业、内行;
ⅲ)原理、依据:正确、明确;
ⅳ)表述:简明,关键步骤要列出;
ⅴ)忌:外行话,专业术语不明确,表述混乱,冗长。
2. 模型求解:
a. 需要建立数学命题时:
命题叙述要符合数学命题的表述规范,尽可能论证严密。b. 需要说明计算方法或算法的原理、思想、依据、步骤。
若采用现有软件,说明采用此软件的理由,软件名称。c. 计算过程,中间结果可要可不要的,不要列出。
d. 设法算出合理的数值结果。
3. 结果分析、检验;模型检验及模型修正;结果表示:
a. 最终数值结果的正确性或合理性是第一位的;
b. 对数值结果或模拟结果进行必要的检验;
结果不正确、不合理、或误差大时,分析原因, 对算法、计算方法、或模型进行修正、改进。
c. 题目中要求回答的问题,数值结果,结论,须一一列出;
d. 列数据问题:考虑是否需要列出多组数据,或额外数据对数据进行比较、分析,为各种方案的提出提供依据;
e. 结果表示:要集中,一目了然,直观,便于比较分析。
▲ 数值结果表示:精心设计表格;可能的话,用图形图表形式。
▲ 求解方案,用图示更好。
模型评价及其优缺点:对本文用到的数学模型进行评价,再对其模型本身进行评价,优点多,缺点少。
模型推广:对本文建立的数学模型进行推广应用到其他领域,进行说明。
参考文献:按照参考文献格式来写,进行写档次较高的文献,与本文相关较大的,引用的数据网站也可以写进来。
附录:包括模型建立和求解中未放完的图和表,模型的求解程序代码等。
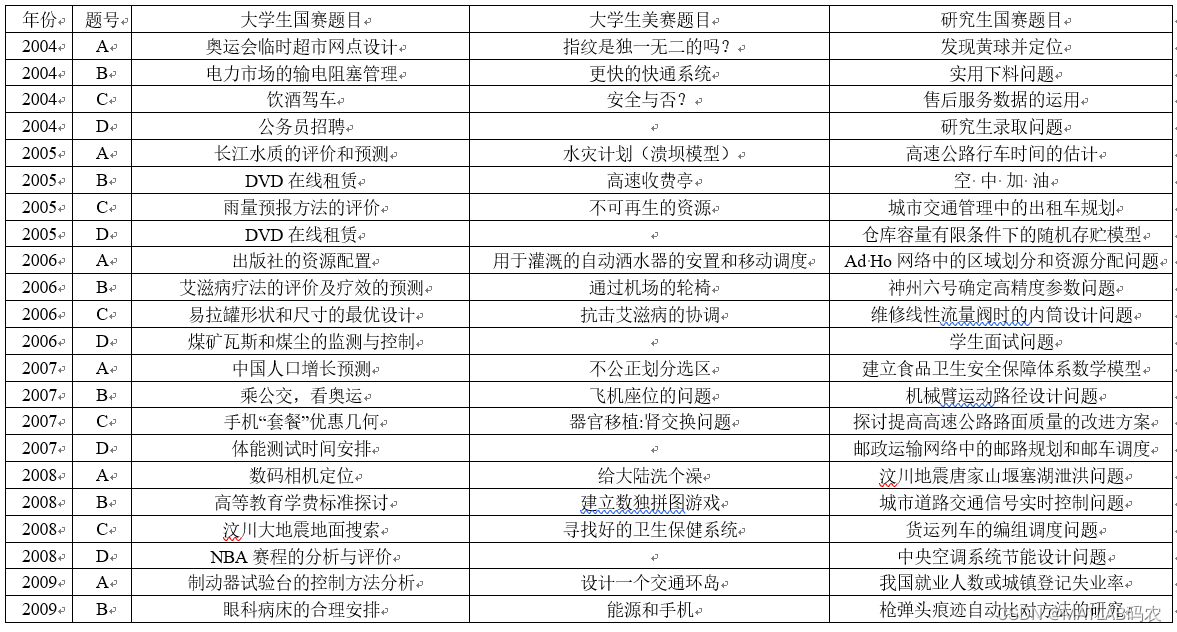
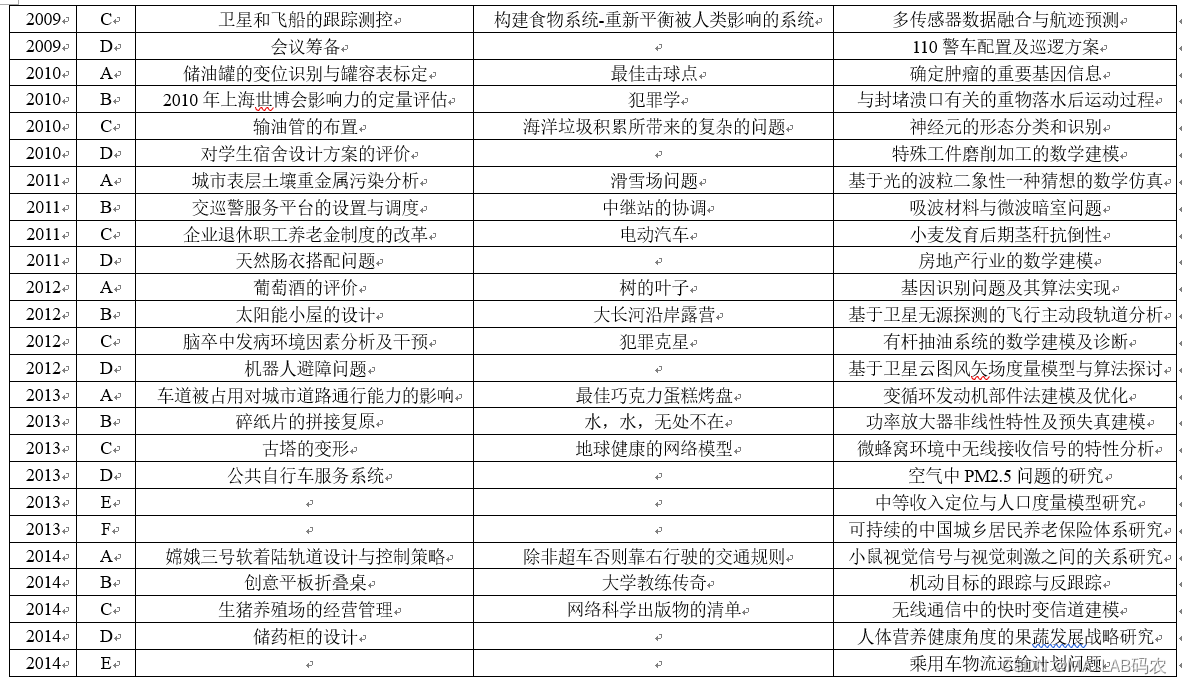
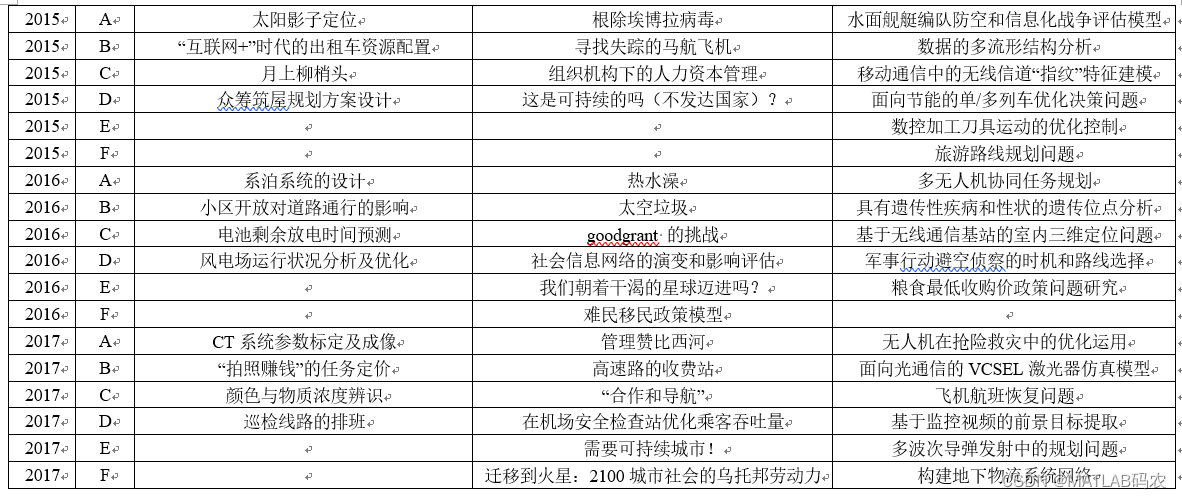
6. 历年数学建模竞赛赛题:
版权归原作者 MATLAB码农 所有, 如有侵权,请联系我们删除。