Leetcode 刷题笔记(二十九) ——动态规划篇之子序列问题：编辑距离

文章目录

系列文章目录

一、 数组类型解题方法一：二分法
二、数组类型解题方法二：双指针法
三、数组类型解题方法三：滑动窗口
四、数组类型解题方法四：模拟
五、链表篇之链表的基础操作和经典题目
六、哈希表篇之经典题目
七、字符串篇之经典题目
八、字符串篇之 KMP
九、解题方法：双指针
十、栈与队列篇之经典题目
十 一、栈与队列篇之 top-K 问题
十 二、二叉树篇之二叉树的前中后序遍历
十 三、二叉树篇之二叉树的层序遍历及相关题目
十 四、二叉树篇之二叉树的属性相关题目
十 五、 二叉树篇之二叉树的修改与构造
十 六、 二叉树篇之二叉搜索树的属性
十 七、二叉树篇之公共祖先问题
十 八、二叉树篇之二叉搜索树的修改与构造
十 九、回溯算法篇之组合问题
二 十、回溯算法篇之分割、子集、全排列问题
二十一、贪心算法篇之入门题目
二十二、贪心算法篇之进阶题目
二十三、动态规划篇之基础题目
二十四、动态规划篇之背包问题：01背包
二十五、动态规划篇之背包问题：完全背包
二十六、动态规划篇之经典问题：打家劫舍
二十七、动态规划篇之买股票问题（一）
二十八、动态规划篇之子序列问题：连续子序列和不连续子序列
更新中 … …

前言

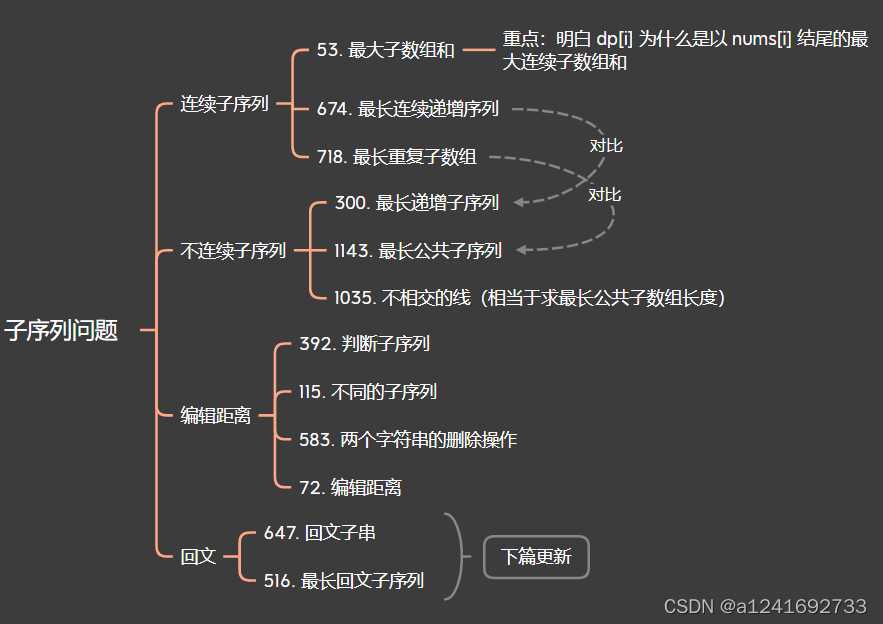
前三道题是理解困难题目编辑距离的基础。
刷题路线来自 ：代码随想录

题录

392. 判断子序列

Leetcode 链接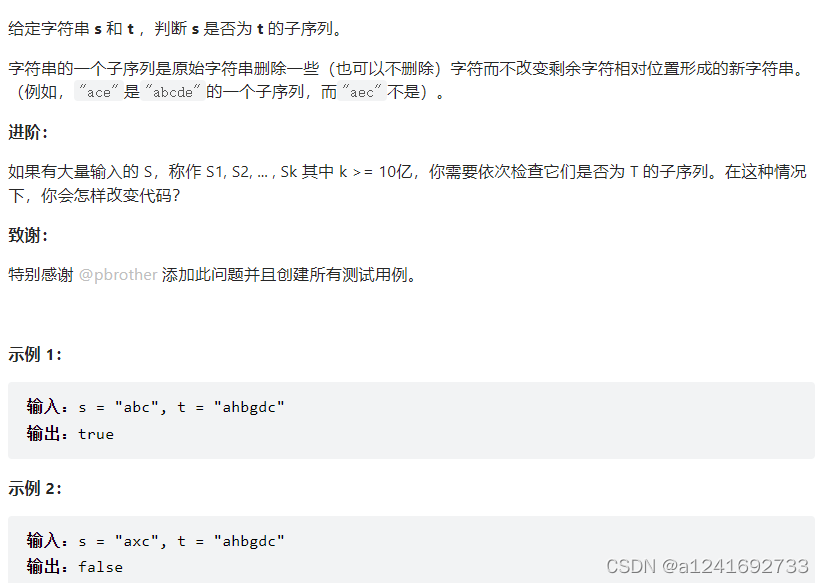

题解：
还是求公共子序列，只不过这里 s 连续，t 不连续，可以像上篇一样 dp数组 记录公共子序列长度，最后判断一下长度是否等于 s 长度，也可以直接使用一个 boolean 类型的 dp 数组，这里使用后者。
状态 dp[i][j]：表示以 i - 1 结尾的 s 子串是不是 t 的[0, j] 区间的子串 的子序列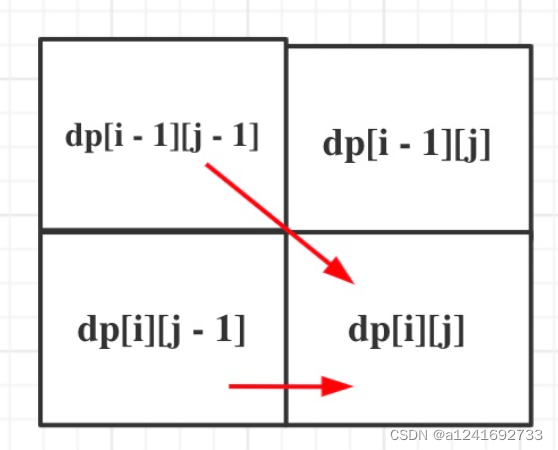

递推公式：
如果 s.charAt(i - 1) == t.charAt(j - 1)，dp[i][j] = dp[i - 1][j - 1]
否则 dp[i][j] = dp[i][j - 1]; 因为要找 s 是不是 t 的子串，某个状态的 s 为 [0, i - 1] 的子串，且不能更改，所以只能缩短 t 串的区间，根据本层前边的状态得出当前状态的值。

初始化：第一行初始化为 true。

classSolution{publicbooleanisSubsequence(String s, String t){int row = s.length();int col = t.length();boolean[][] dp =newboolean[row +1][col +1];// 初始化for(int i =0; i <= col; i++){
            dp[0][i]=true;}for(int i =1; i <= row; i++){for(int j =1; j <= col; j++){if(s.charAt(i -1)== t.charAt(j -1)){
                    dp[i][j]= dp[i -1][j -1];}else{
                    dp[i][j]= dp[i][j -1];}}}return dp[row][col];}}

双指针更快哈哈哈

classSolution{publicbooleanisSubsequence(String s, String t){int i =0;int j =0;while(i < s.length()&& j < t.length()){if(s.charAt(i)== t.charAt(j)){
                i++;} 
            j++;}return i == s.length();}}

115. 不同的子序列

Leetcode 链接

题解：
换个说法，计算 t 在 s 的不连续子串中出现的次数。
t 作为 row，s 作为 col，寻找 t 在 s 中有多少种组合
状态 dp[i][j]：表示 t 下标从0 到 i - 1的子串在 [0, j - 1] 区间 s 的所有子串中有多少种组合方式。
不相等是，t 作为连续串，所以只能根据该层 dp 数组前边的状态得到当前状态的值
手画一遍图就明白递推公式的意思了。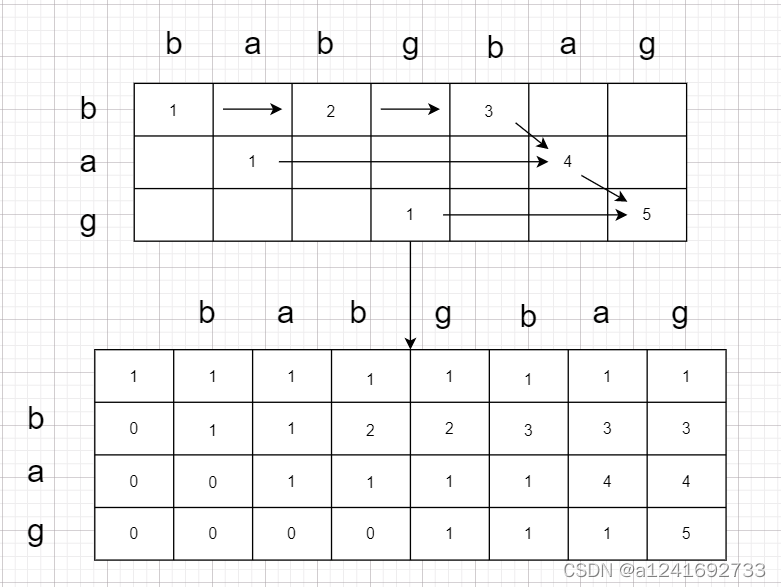

classSolution{publicintnumDistinct(String s, String t){int row = t.length();int col = s.length();int[][] dp =newint[row +1][col +1];for(int i =0; i <= col; i++){
            dp[0][i]=1;}for(int i =1; i <= row; i++){for(int j =1; j <= col; j++){if(t.charAt(i -1)== s.charAt(j -1)){
                    dp[i][j]= dp[i -1][j -1]+ dp[i][j -1];}else{
                    dp[i][j]= dp[i][j -1];}}}return dp[row][col];}}

583. 两个字符串的删除操作

Leetcode 链接

题解：
方式一：同上篇提到的 1143. 最长公共子序列，计算出最长公共子序列长度，然后用总分长度减去公共长度就是需要删除的长度

classSolution{publicintminDistance(String word1, String word2){int row = word1.length();int col = word2.length();int[][] dp =newint[row +1][col +1];for(int i =1; i <= row; i++){for(int j =1; j <= col; j++){if(word1.charAt(i -1)== word2.charAt(j -1)){
                    dp[i][j]= dp[i -1][j -1]+1;}else{
                    dp[i][j]= Math.max(dp[i -1][j], dp[i][j -1]);}}}return row + col -2* dp[row][col];}}

方式二：
dp[i][j] 就表示 [0, i - 1] 的 word1 和 [0, j - 1] 的 word2 需要删除的最少长度
递推公式：每次比较 word1.charAt(i - 1) 和 word2.charAt(j - 1)
如果相等：dp[i][j] 取 dp[i - 1][j - 1]，因为不用删除
如果不相等：dp[i][j] 取 dp[i - 1][j] 和 dp[i][j - 1] 中最小的值加一；用一个例子解释：
如 “sea” 和 “eat” 中 i = j = 3 时，a 和 t 不同，去 “aea” 和 “ea” 、“se” 和 “eat” 这两个状态取最小的一种状态 加上 1（1 表示新增的字符，不相等应该删除）。

classSolution{publicintminDistance(String word1, String word2){int row = word1.length();int col = word2.length();int[][] dp =newint[row +1][col +1];for(int i =0; i <= row; i++){
            dp[i][0]= i;}for(int i =1; i <= col; i++){
            dp[0][i]= i;}for(int i =1; i <= row; i++){for(int j =1; j <= col; j++){if(word1.charAt(i -1)== word2.charAt(j -1)){
                    dp[i][j]= dp[i -1][j -1];}else{
                    dp[i][j]= Math.min(dp[i -1][j], dp[i][j -1])+1;}}}return dp[row][col];}}

72. 编辑距离

Leetcode 链接

题解：

if(word1[i -1]== word2[j -1])
    不操作
if(word1[i -1]!= word2[j -1])
    增
    删
    换

增和删操作次数是一样的，如 ros 和 rs，给 rs 中间增添一个 o，或者删除 ros 中间的 o。
状态 dp[i][j]：表示以下标 i-1 为结尾的字符串 word1，和以下标 j-1 为结尾的字符串 word2 的编辑距离
递推公式：
不操作：[i][j] = dp[i - 1][j - 1]
操作：
替换：dp[i][j] = dp[i - 1][j - 1] + 1，新增的两个字符其中一个替换为另一个
增删：dp[i][j - 1] + 1、dp[i- 1][j] + 1，word1 和 word2 一个不动，操作另一个
取三者中操作次数最小的

classSolution{publicintminDistance(String word1, String word2){int row = word1.length();int col = word2.length();int dp[][]=newint[row +1][col +1];for(int i =0; i <= row; i++){
            dp[i][0]= i;}for(int i =0; i <= col; i++){
            dp[0][i]= i;}for(int i =1; i <= row; i++){for(int j =1; j <= col; j++){if(word1.charAt(i -1)== word2.charAt(j -1)){
                    dp[i][j]= dp[i -1][j -1];}else{
                    dp[i][j]= Math.min(Math.min(dp[i][j -1], dp[i -1][j]), dp[i -1][j -1])+1;}}}return dp[row][col];}}