LSTM单步时间序列预测文章(联系方式在此文章):
(511条消息) 时间序列预测——LSTM模型(附代码实现)_lstm预测模型_噜噜啦啦咯的博客-CSDN博客
模型原理
长短时记忆网络( Long short-term memory,LSTM )是一种循环神经网络 (Recurrent neural network, RNN)的特殊变体,具有“门”结构,通过门单元的逻辑控制决定数据是否更新或是选择丢弃,克服了 RNN 权重影响过大、容易产生梯度消失和爆炸的缺点,使网络可以更好、更快地收敛,能够有效提高预测精度。LSTM 拥有三个门, 分别为遗忘门、输入门、输出门,以此决定每一时刻信息记忆与遗忘。输入门决定有多少新的信息加入到细胞当中,遗忘门控制每一时刻信息是否会被遗忘,输出门决定每一时刻是否有信息输出。其基本结构如图所示。
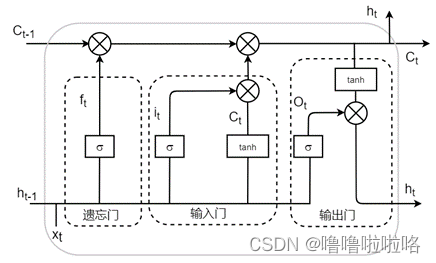
公式如下:
(1)遗忘门
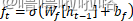
(2)输入门
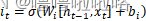
(3)单元
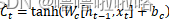
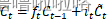
(4)输出门
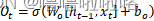
(5)最终输出
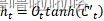
模型实现
导入所需要的库
import matplotlib.pyplot as plt
from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM,Dense,Dropout
from numpy import concatenate
from sklearn.metrics import mean_squared_error,mean_absolute_error,r2_score
from math import sqrt
设置随机数种子
import tensorflow as tf
tf.random.set_seed(2)
导入数据集
data = pd.read_csv(r'C:\Users\26255\Desktop\data.csv')
数据可视化
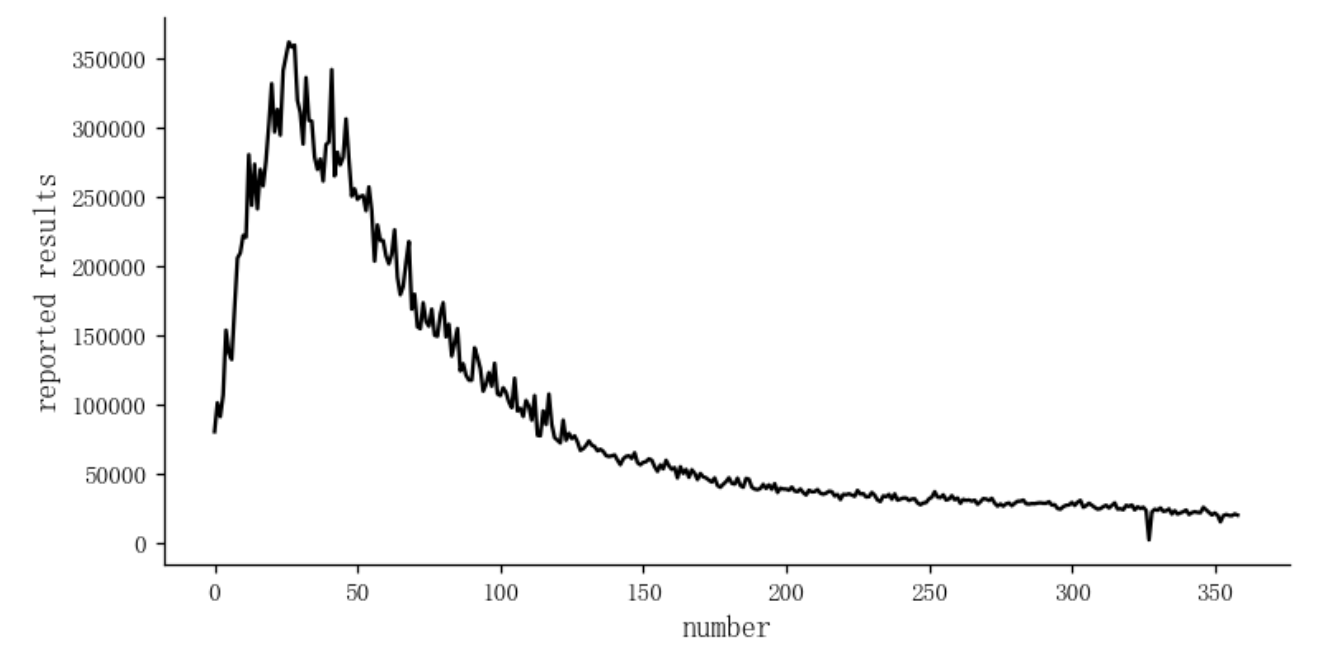
数据处理
归一化处理
# 特征的归一化处理
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
将时间序列转换为监督学习问题
#定义series_to_supervised()函数
#将时间序列转换为监督学习问题
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
#Frame a time series as a supervised learning dataset.
#Arguments:
#data: Sequence of observations as a list or NumPy array.
#n_in: Number of lag observations as input (X).
#n_out: Number of observations as output (y).
#ropnan: Boolean whether or not to drop rows with NaN values.
#Returns:
#Pandas DataFrame of series framed for supervised learning.
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = list(), list()
# input sequence (t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# forecast sequence (t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# put it all together
agg = concat(cols, axis=1)
agg.columns = names
# drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg
设置步数
n_in = 10
n_out = 10
n_out_fin = n_out - 1
reframed = series_to_supervised(scaled, n_in, n_out)
划分训练集和测试集
values = reframed.values
trainNum = int(len(values) * 0.7) # 350
train = values[:trainNum, :] # 前350
test = values[trainNum:, :] # 后150
改变数据维度
print(train_X.shape, train_y.shape)
print(test_X.shape, test_y.shape)

搭建LSTM模型
初始化LSTM模型
设置神经元核心的个数,迭代次数,优化器等等
# define model
model = Sequential()
model.add(LSTM(100, return_sequences=True))
model.add(Dropout(0.1))
model.add(LSTM(100))
model.add(Dropout(0.1))
model.add(Dense(n_out))
model.compile(optimizer='adam', loss='mse', metrics=['mse'])
history = model.fit(train_X, train_y, epochs=100, batch_size=10, validation_data=(test_X, test_y), verbose=2,shuffle=False)
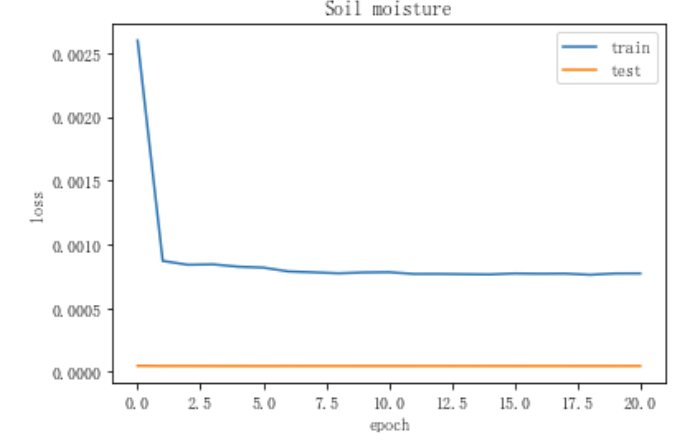
画出损失函数
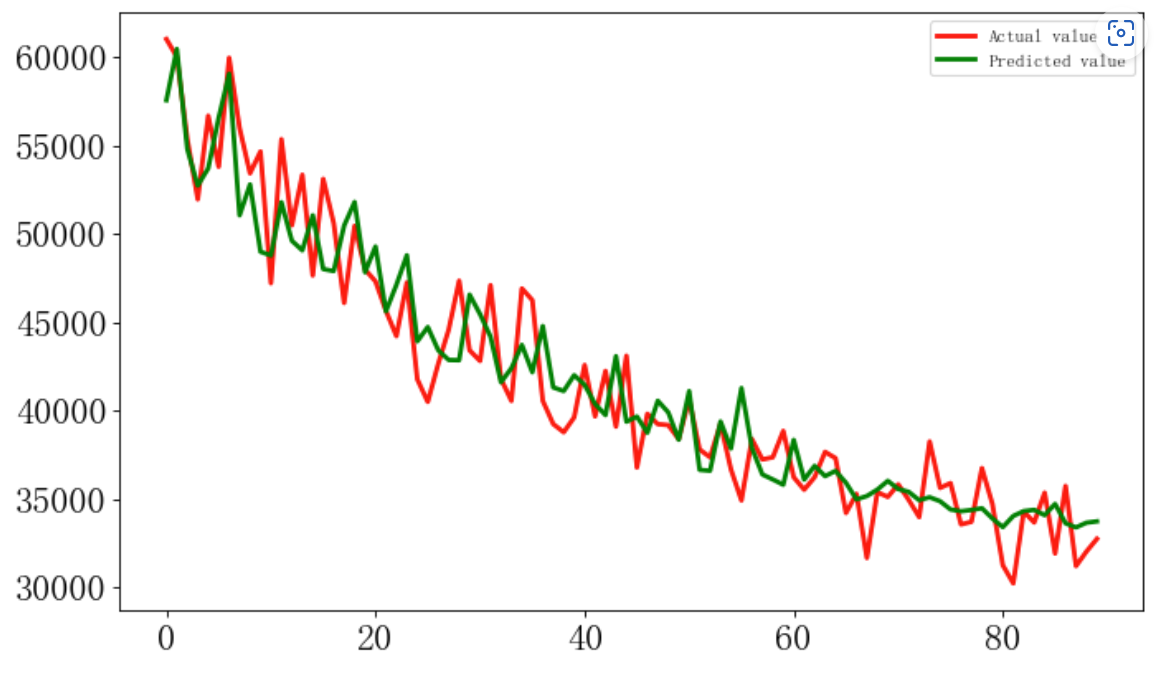
模型预测
y_predict = model.predict(test_X)
评价指标
# 回归评价指标
# calculate MSE 均方误差
mse = mean_squared_error(inv_y, inv_y_predict[:, n_out_fin])
# calculate RMSE 均方根误差
rmse = sqrt(mean_squared_error(inv_y, inv_y_predict[:, n_out_fin]))
# calculate MAE 平均绝对误差
mae = mean_absolute_error(inv_y, inv_y_predict[:, n_out_fin])
# calculate R square
r_square = r2_score(inv_y, inv_y_predict[:, n_out_fin])
print('均方误差MSE: %.6f' % mse)
print('均方根误差RMSE: %.6f' % rmse)
print('平均绝对误差MAE: %.6f' % mae)
print('R_square: %.6f' % r_square)

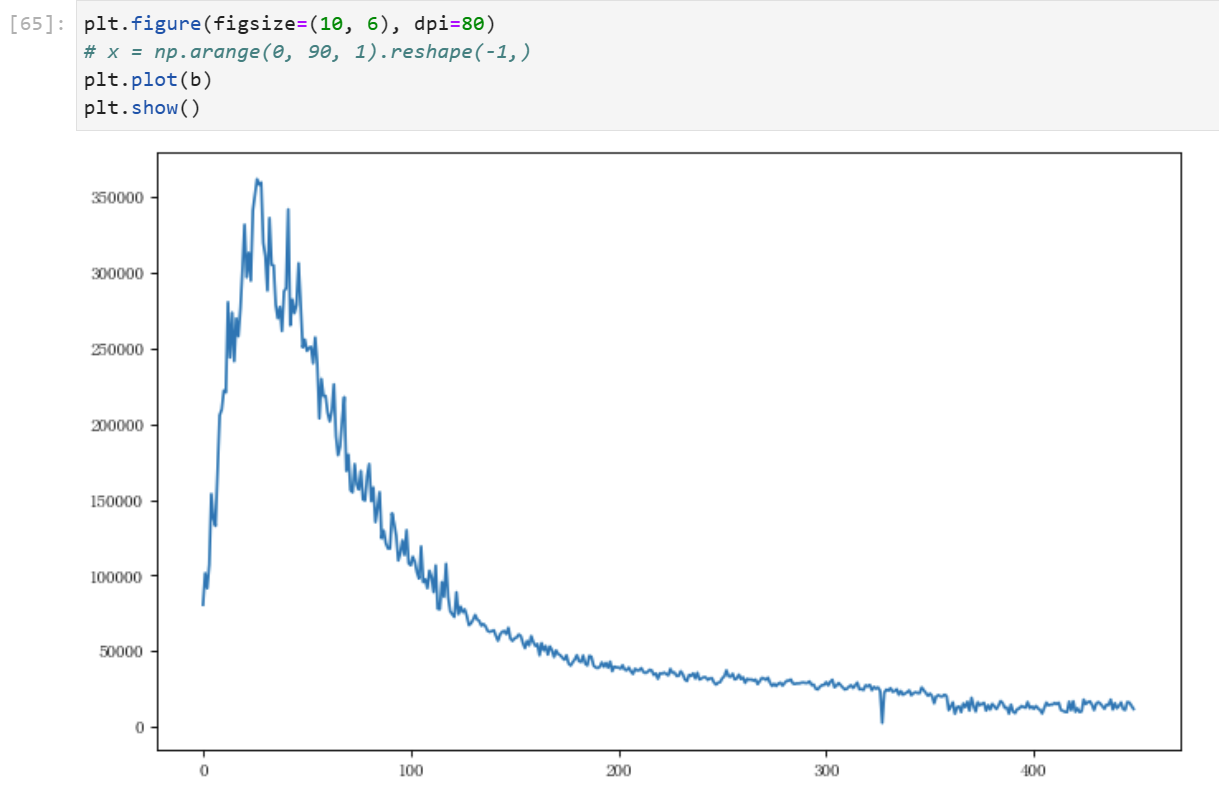
滚动预测
传入最新收集到的数据,进行往后滚动预测,得到未来数据,与原数据进行拼接并将其可视化
获得置信区间
可以计算预测误差的标准差,然后利用该标准差计算置信区间。
标准差
标准差是指一组数据的离散程度的度量,它表示数据集中的数据偏离平均值的程度。标准差越大,表示数据越分散;标准差越小,表示数据越集中。
计算标准差的具体步骤如下:
计算平均值。将数据集中的所有数值相加,然后除以数据的个数,即可得到平均值。
计算每个数据与平均值的差值。将数据集中的每个数值与平均值进行减法运算,得到每个数据与平均值之间的差值。
计算差值的平方。将第二步得到的差值依次平方,即得到每个数据与平均值之间的差值的平方。
计算平方和。将第三步得到的差值的平方相加,即得到平方和。
计算方差。将平方和除以数据的个数,即得到方差。
计算标准差。将方差的平方根即为标准差。
用公式表示,假设有N个数据,数据集为{x1, x2, ..., xn},平均值为μ,标准差为σ,则:
μ = (x1 + x2 + ... + xn) / N
σ = sqrt[( (x1 - μ)^2 + (x2 - μ)^2 + ... + (xn - μ)^2 ) / N]
其中,sqrt表示平方根运算。
具体步骤
选择合适的回归模型。
计算模型的预测误差。使用模型来预测每天结果,然后将实际结果数量与预测结果数量进行比较,计算误差。计算每日的误差后,可以计算误差的标准差,该标准差代表了模型的预测误差大小。
计算置信区间。使用标准正态分布表来查找95%置信水平对应的z值,通常是1.96。然后将该值乘以预测误差的标准差,从而得到置信区间的半宽度。最后,将半宽度加上和减去预测结果的平均值,即可得到95%置信区间的上限和下限。
举个例子,如果使用线性回归模型拟合数据,得到每日报告结果数量的预测值为y=10+2x,其中x是从2023年1月1日到3月1日的天数。如果在过去的记录中,每日报告结果数量的标准差为s=3,那么95%置信区间的上限和下限可以计算如下:
z=1.96 (95%置信水平对应的z值)halfwidth = z * s = 1.96 * 3 = 5.88 (置信区间的半宽度)预测结果的平均值为y=10+2*60=130置信区间的上限为130+5.88=135.88置信区间的下限为130-5.88=124.12
因此,该模型预测2023年3月1日报告结果数量的95%置信区间为[124.12, 135.88]。这意味着,我们可以合理地期望2023年3月1日的报告结果数量在这个区间内。
应用实例
将其应用在此数据集中,得到预测误差的标准差:
std_error = np.std(train_y - model.predict(train_X))
print("Standard deviation of prediction error: ", std_error)
计算得到的标准差即为预测误差的标准差。
最后,我们可以利用该标准差来计算置信区间。假设我们希望计算95%的置信区间,我们可以使用scipy.stats.norm库中的ppf()函数来计算正态分布的分位数,然后计算置信区间的上下限:
from scipy.stats import norm
z = norm.ppf(0.975)
lower_bound = future_predict[:, n_out_fin] - z * std_error
upper_bound = future_predict[:, n_out_fin] + z * std_error
print("95% confidence interval: ({:.2f}, {:.2f})".format(lower_bound[0], upper_bound[0]))
其中,ppf()函数的参数0.975表示95%置信度对应的分位数。计算得到的上下限即为置信区间。
版权归原作者 噜噜啦啦咯 所有, 如有侵权,请联系我们删除。