专栏: 蓝桥杯——每日四道编程题(两道真题+两道模拟)
“蓝桥杯就要开始了,这些题刷到就是赚到”
₍ᐢ..ᐢ₎♡
另一个专栏: 蓝桥杯——每日四道填空题(两道真题+两道模拟题)
第一道真题(2019省赛A组):修改数组
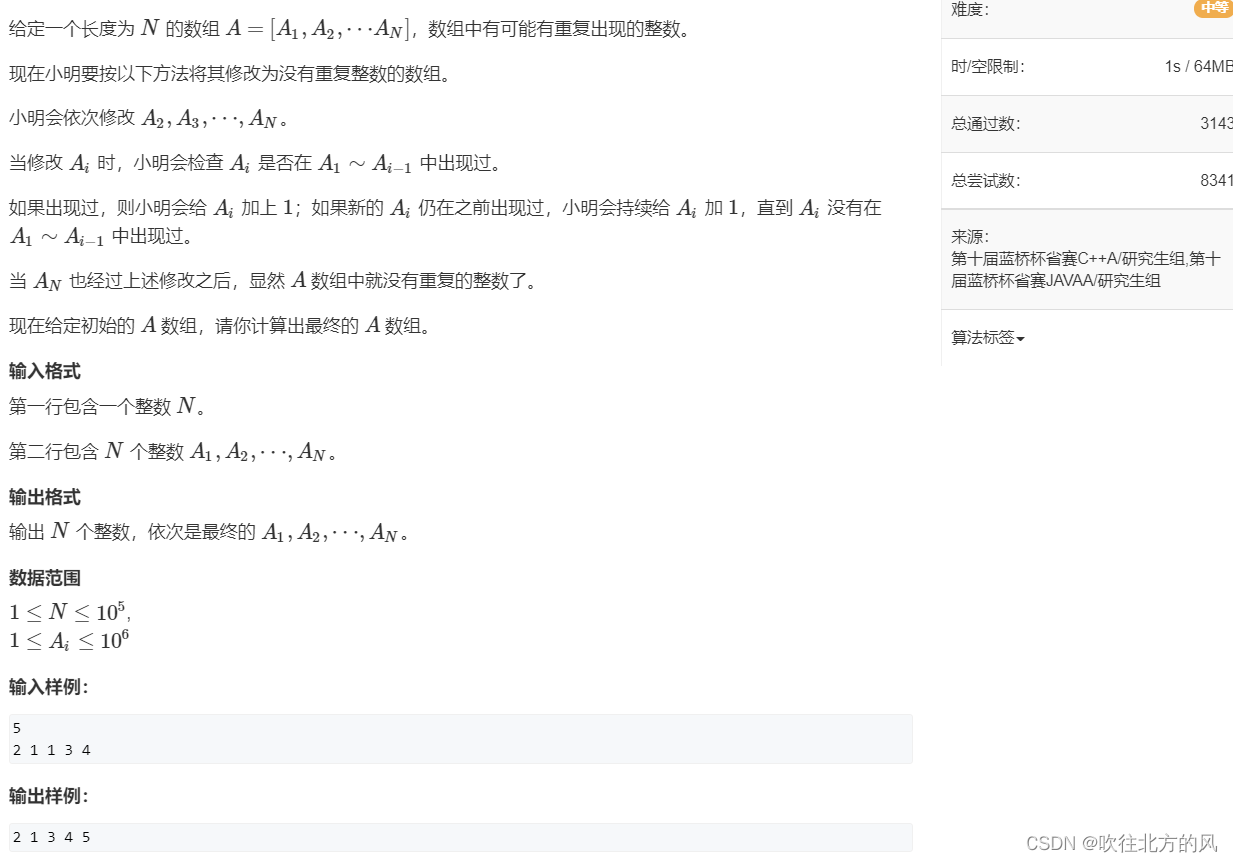
这题看着和双指针算法这道题很像: 最长连续不重复子序列
因此我就用这个方法做了一下~
#include <iostream>
using namespace std;
int a[100005] , b[1000005];
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> a[i];
while (b[a[i]] != 0)
{
a[i] += 1;
}
b[a[i]]++;
cout << a[i] << ' ';
}
return 0;
}
结果只AC了80%,就超时了。
这题应采用并查集来优化(说实话,我是没想到)
它可以把数据合并成一个个集合(父节点不同),如果要将重复数改变成不重复的数,只需要将其更新成集合的父节点就行,很巧妙。
#include <iostream>
using namespace std;
const int N = 1000005;
int p[N];
int n;
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin >> n;
for(int i = 1 ; i <= N ; i++) p[i] = i; //初始化
for(int i = 1 ; i <= n ; i++)
{
int x;
cin >> x;
x = find(x);
cout << x << " ";
p[x] = x + 1; //更新父节点,为了后面改变重复数
}
return 0;
}
第二道真题(2019年省赛B组):完全二叉树的权值


特地去刷了一道二叉树的题,别忘了就行~
完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
这题要涉及完全二叉树结点数和层数的关系:
我们知道结点个数为n 的满二叉树的深度为:
个数为n的完全二叉树的深度为: (向下取整)
#include<bits/stdc++.h>
using namespace std;
int sum[10008] = {0};
int main()
{
int n;
int w;
int ans;
int maxn = 0;
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> w;
int d = floor(log(2*i)/log(2)); //c++里面log函数都是以10为底的,这里要手动把以2为底转成10为底
sum[d] += w;
}
for(int i = 1; i < 10008; i++) //从第一层开始逐层比较,保证最大且深度最小的值输出
{
if(sum[i] > maxn)
{
maxn = sum[i];
ans = i;
}
}
cout << ans;
return 0;
}
第三道模拟题(2022年省赛B组第三次模拟)
题目描述:小蓝准备在一个空旷的场地里面滑行,这个场地的高度不一,小蓝用一个 n 行 m 列的矩阵来表示场地,矩阵中的数值表示场地的高度。
如果小蓝在某个位置,而他上、下、左、右中有一个位置的高度(严格)低于当前的高度,小蓝就可以滑过去,滑动距离为 1 。
如果小蓝在某个位置,而他上、下、左、右中所有位置的高度都大于等于当前的高度,小蓝的滑行就结束了。
小蓝不能滑出矩阵所表示的场地。
小蓝可以任意选择一个位置开始滑行,请问小蓝最多能滑行多远距离。输入第一行包含两个整数 n, m,用一个空格分隔。
接下来 n 行,每行包含 m 个整数,相邻整数之间用一个空格分隔,依次表示每个位置的高度。输出一行包含一个整数,表示答案。
对于 30% 评测用例,1 <= n <= 20,1 <= m <= 20,0 <= 高度 <= 100。
对于所有评测用例,1 <= n <= 100,1 <= m <= 100,0 <= 高度 <= 10000。
这题数据范围比较小,可以用暴力+DFS进行逐一查找。
代码来源:第十四届蓝桥杯第三期模拟赛 C/C++ B组 原题与详解_蓝桥杯模拟赛第三期_Ggggggtm的博客-CSDN博客
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
const int N = 110;
int n, m;
int g[N][N];
bool f[N][N];
int dx[4] = { -1, 0, 1, 0 }, dy[4] = { 0, 1, 0, -1 };
int dfs(int x, int y)
{
int res = 0;
for (int i = 0; i < 4; i++)
{
int a = x + dx[i], b = y + dy[i];
if (a >= 1 && a <= n && b >= 1 && b <= m && !f[a][b] && g[x][y] > g[a][b])
{
f[a][b] = true;
res = max(res, dfs(a, b) + 1); //最后到了不能走了,就开始递归回去,每次+1;这里用max函数求最长的递归路径,即最大滑雪长度。
//还原现场
f[a][b] = false;
}
}
return res;
}
int main()
{
scanf("%d%d", &n, &m);
int res = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &g[i][j]);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
f[i][j] = true; //表示当前位置已经走过
res = max(res, dfs(i, j));
//还原现场
f[i][j] = false;
}
cout << res + 1 << "\n";
return 0;
}
第三道模拟题(2022年省赛B组第二次模拟)
【问题描述】
n 个小朋友正在做一个游戏,每个人要分享一个自己的小秘密。
每个小朋友都有一个 1 到 n 的编号,编号不重复。
为了让这个游戏更有趣,老师给每个小朋友发了一张卡片,上面有一个 1 到 n 的数字,每个数字正好出现一次。
每个小朋友都将自己的秘密写在纸上,然后根据老师发的卡片上的数字将秘密传递给对应编号的小朋友。如果老师发给自己的数字正好是自己的编号,这个秘密就留在自己手里。
小朋友们拿到其他人的秘密后会记下这个秘密,老师会再指挥所有小朋友将手中的秘密继续传递,仍然根据老师发的卡片上的数字将秘密传递给对应编号的小朋友。
这样不断重复 n 次。
现在,每个小朋友都记下了很多个秘密。
老师现在想找一些小朋友,能说出所有秘密,请问老师最少要找几个小朋友?
【输入格式】
输入的第一行包含一个整数 n。
第二行包含 n 个整数 a[1], a[2], …, a[n],相邻的整数间用空格分隔,分别表示编号 1 到 n 的小朋友收到的数字。
【输出格式】
输出一行包含一个整数,表示答案。
【样例输入】
6
2 1 3 5 6 4
【样例输出】
3
【样例说明】
最终小朋友 1, 2 互相知道了对方的秘密,小朋友 3 只知道自己的秘密,小朋友 4, 5, 6 互相知道了对方的秘密。
至少要找 3 个小朋友才能说出所有秘密。
【评测用例规模与约定】
对于 30% 的评测用例,2 <= n <= 30。
对于 60% 的评测用例,2 <= n <= 1000。
对于所有评测用例,2 <= n <= 100000。
由于卡片不会重复,所以答案就是环的个数
因为经过 n 轮循环后,环中的每个小朋友都知道环中所有人的秘密,所以从每个环中找出一人即可
#include <iostream>
using namespace std;
const int N = 100005;
int n, tmp, ans = 0;;
int a[N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= n; i++) {
if (a[i] != 0) ans++;
int idx = i;
while (a[idx]) {
tmp = a[idx];
a[idx] = 0;
idx = tmp;
}
}
cout << ans << endl;
return 0;
}

版权归原作者 吹往北方的风 所有, 如有侵权,请联系我们删除。