JavaScript算法描述【回溯算法】|括号生成|子集|电话号码的字母组合|全排列|单词搜索

文章目录

回溯算法

回溯算法(back tracking)是一种类似尝试算法，按选优条件向前搜索，主要是在搜索尝试过程中寻找问题的解，以达到目标，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。换句话说，找到一条路往前走，能走就继续往前，不能走就算了，掉头换条路。相对于动态规划，这部分的内容相对于简单些。

回溯的处理思想，和枚举搜索有点类似，通过枚举找到所有满足期望的值。为了有规律地枚举所有的解，可以把问题拆解为多个小问题。每个小问题，我们都会面对一个岔路口，选择一条发现此路不通的时，就往回走，走到另一个岔路口。

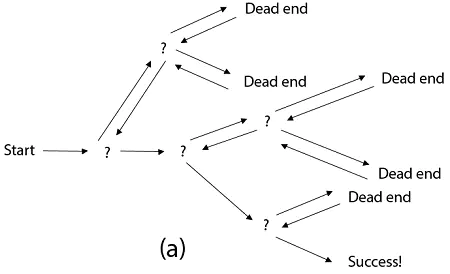
本章节分为 2 个部分，选取了比较经典的算法题，希望可以帮助到同学们学会解决回溯相关的算法题。

• Part 1 - 括号生成- 子集- 电话号码的字母组合
• Part 2 - 全排列- 单词搜索

括号生成、子集和电话号码的字母组合

括号生成

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

示例

例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

方法一 回溯法（实现一）

思路

我们知道，有且仅有两种情况，生成的括号序列不合法

• 我们不停的加左括号，其实如果左括号超过 n 的时候，它肯定不是合法序列了。因为合法序列一定是 n 个左括号和 n 个右括号。
• 如果添加括号的过程中，如果右括号的总数量大于左括号的总数量了，后边不论再添加什么，它都不可能是合法序列了。

基于上边的两点，我们只要避免它们，就可以保证我们生成的括号一定是合法的了。

详解

1. 采用回溯法，即把问题的解空间转化成了图或者树的结构表示，然后，使用深度优先搜索策略进行遍历，遍历的过程中记录和寻找所有可行解或者最优解。
2. 如果自定义的字符串长度足够且走到这里，那么就说明这个组合是合适的，我们把它保存。
3. 否则，递归执行添加左括号，添加右括号的操作。
4. 递归结束条件为结果字符串长度等于左右括号的总个数（2n），则返回最终结果。

代码

/**
 * @param {number} n
 * @return {string[]}
 */constgenerateParenthesis=n=>{const res =[];const gen =(str ='', l =0, r =0)=>{// 如果自定义的字符串长度足够且走到这里，那么就说明这个组合是合适的if(str.length ===2* n){
      res.push(str);return;}// 下面的逻辑：左括号必须出现在右括号的前面// 只有在 l >= n 的 时候，才不能添加左括号，其他都可添加if(l < n){gen(`${str}(`, l +1, r);}// 如果右括号没有左括号多，我们就可以添加一个右括号if(r < l){gen(`${str})`, l, r +1);}};gen();return res;};

复杂度分析

我们的复杂度分析依赖于理解 generateParenthesis(n) 中有多少个元素。这个分析需要更多的背景来解释，但事实证明这是第 n 个卡塔兰数 \dfrac{1}{n+1}\binom{2n}{n}n+11(n2n)，这是由 \dfrac{4^n}{n\sqrt{n}} nn4n 渐近界定的。

• 时间复杂度：O(\dfrac{4^n}{\sqrt{n}})O(n4n)，在回溯过程中，每个有效序列最多需要 n 步。
• 空间复杂度：O(\dfrac{4^n}{\sqrt{n}})O(n4n)，如上所述，并使用 O(n)O(n) 的空间来存储序列。

方法二 回溯法（实现二）

思路

整体的实现思路也是回溯法，也是递归来实现该思路，唯一不同的是，递归的结束条件是左右括号都消费尽。

详解

1. 采用回溯法，即把问题的解空间转化成了图或者树的结构表示，然后，使用深度优先搜索策略进行遍历，遍历的过程中记录和寻找所有可行解或者最优解。
2. 首先，先从左括号开始填充。
3. 然后，填充右括号，保证两类括号数目一致，平衡。
4. 递归结束条件为左右括号均消费尽，则输出结果。

代码

/**
 * @param {number} n
 * @return {number}
 */constgenerateParenthesis=n=>{const res =[];// left :左括号个数， right:右括号个数functionhelper(left, right, max, str){if(left === max && right === max){
      res.push(str);return;}// 先从左括号开始填充if(left < max){helper(left +1, right, max,`${str}(`);}// 保证两类括号数目一致if(left > right){helper(left, right +1, max,`${str})`);}}helper(0,0, n,'');return res;};

复杂度分析

本方法也是使用回溯法，只是具体实现方式不同，因此，复杂度也是一样的。

• 时间复杂度：O(\dfrac{4^n}{\sqrt{n}})O(n4n)

在回溯过程中，每个有效序列最多需要 nn 步。

• 空间复杂度：O(\dfrac{4^n}{\sqrt{n}})O(n4n)

如上所述，并使用 O(n)O(n) 的空间来存储序列。

子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

方法一 回溯算法

思路

设置初始二维数组[[]]，依次把每个数加入到数组中的每一个元素中，并保留原来的所有元素。

详解

1. 初始化二维数组来存储所有子集；
2. 使用双层遍历，外层遍历 nums 数组，内层遍历二维数组，将每个元素与二维数组每项合并，并保留二维数组原有的元素
3. 并将得到的新子集与二维数组元素合并，最后得到所有子集；

例如：输入 nums = [1, 2, 3] 初始化二维数组存储所有子集 result = [[]] 然后遍历 nums, 1 添加到[], 结果为 [[], [1]]; 2 添加到[], [1], 结果为 [[], [1], [2], [1, 2]]; 3 添加到[], [1], [2], [1, 2], 结果为 [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]];

代码

constsubsets=(nums)=>{let result =[[]];// 初始化二维数组for(let i of nums){const temp =[];for(let k of result){
      temp.push(k.concat(i));// 依次把每个元素添加到数组中}
    result = result.concat(temp);}return result;}

复杂度分析

• 时间复杂度：O(2^n)O(2n)

根据上述算法，每次循环 result 数组的次数为 2^{(n - 1)}2(n−1)， 则计算总数为 1 + 2^1 + 2^2 + … + 2^{(n-1)}1+21+22+…+2(n−1)，根据等比数列计算公式得到循环总次数为 2^n - 12n−1，所以时间复杂度为 O(2^n)O(2n)。

• 空间复杂度：O(2^n)O(2n)

根据排列组合原理，子集包含一个数字的情况所耗费的存储空间为 C_n^1 * 1Cn1∗1 ，包含两个数字所耗费的存储空间为 C_n^2 * 2Cn2∗2 ，根据算法得出 共需要 C_n^0 + C_n^1 + 2 * C_n^2 + … + (n - 1) * C_n^{n - 1} + n * C_n^nCn0+Cn1+2∗Cn2+…+(n−1)∗Cnn−1+n∗Cnn 个存储空间，根据排列组合公式求和可得需要 n*2^{n-1} + 1n∗2n−1+1 个额外存储空间， 所以算法空间复杂度为 O(2^n)O(2n)。

方法二 二进制表示法

思路

从数学角度看，求子集其实是一个排列组合问题，比如 nums = [1, 2, 3]，存在四种情况：

1. 都不选，情况共有 C_3^0= 1C30=1种
2. 只选 1 个数，情况共有 C_3^1 = 3C31=3种
3. 选 2 个数，情况共有 C_3^2 = 3C32=3 种
4. 全选，情况共有 C_3^3 = 1C33=1种

落到数组中的每个数字，都有两种可能，选与不选，我们用 1 标识选，用 0 标识不选。 则 [] 表示为 000，[1, 2, 3] 表示为 111，我们通过转化为二进制表示法，遍历 000 - 111 的所有组合，即可求出所有子集。

详解

1. 根据上述分析，我们得出加入数组为 nums，则针对每位存在选与不选两种情况，那么所有组合数为 2 ^ {length}2length 个。
2. 针对每一种组合情况，我们可以取出该二进制表示法中的每一位，如 110，我们分别通过向右移位并和 1 求与，判断最低为的值为 0 或者 1。
3. 如果得到结果为 1，那么表示该位表示的数字在原数组中被选中，存入暂存数组，一轮遍历后即可获得该组子集的数字组合。将所有子集数字组合一起存入结果数组，即求出所有子集。

代码

constsubsets=(nums)=>{// 子集的数量const len = nums.length;const setNums = Math.pow(2, len);const result =[];for(let i =0; i < setNums; i++){let temp =[];// 判断该二进制表示法中，每一个位是否存在for(let j =0; j < len; j++){if(1&(i >> j)){// 如果该位为 1，则存入组合数组
        temp.push(nums[j]);}}

    result.push(temp);}return result;};

复杂度分析

• 时间复杂度：O(2^n)O(2n)

一共包含 2^n2n 个组合需要 n * 2^nn∗2n 次计算，所以时间复杂度为 O(2^n)O(2n)。

• 空间复杂度：O(2^n)O(2n)

电话号码的字母组合

给定一个仅包含数字

2-9

的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例

输入："23"

输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

方法一 挨个遍历

思路

利用队列的先进先出的特点，把队列中的第一个元素拿出，再与后面的挨个拼接

a, b, c --> b, c, ad, ae, af --> c, ad, ae, af, bd, be, bf -> …

详解

1. 先在队列中插入一个空字符
2. 取出队列中的第一个元素，与后一位数字对应的字符进行挨个拼接
3. 重复第二步，直到结束

代码

constletterCombinations=function(digits){const map ={2:['a','b','c'],3:['d','e','f'],4:['g','h','i'],5:['j','k','l'],6:['m','n','o'],7:['p','q','r','s'],8:['t','u','v'],9:['w','x','y','z']};if(!digits){return[];}const res =[''];for(let i =0; i < digits.length; i++){const letters = map[digits[i]];const size = res.length;for(let j =0; j < size; j++){const temp = res.shift(0);// 取出第一个元素for(let k =0; k < letters.length; k++){
        res.push(`${temp}${letters[k]}`);// 第一个元素与后一位数字对应的字符进行挨个拼接}}}return res;};

复杂度分析

• 时间复杂度： O(3^m * 4^n)O(3m∗4n)通过数组的 push 我们发现，循环的次数和最后数组的长度是一样的，然而数组的长度有和输入多个3个字母的数目、4个字母的数目有关，得出时间复杂度为 O(3^m * 4^n)O(3m∗4n)其中 mm 为3个字母的数目，nn 为4个字母的数目
• 空间复杂度： O(3^m * 4^n)O(3m∗4n)最后结果的长度和输入的数字有关，得出复杂度为 O(3^m * 4^n)O(3m∗4n)

方法二 回溯

思路

这道题有点排列组合的味道，我们可以穷举所有的可能性，找到所有的可能性

详解

1. 如果还有数字需要被输入，就继续遍历数字对应的字母进行组合 prefix + letter
2. 当发现没有数字输入时，说明已经走完了，得到结果代码

const map ={2:['a','b','c'],3:['d','e','f'],4:['g','h','i'],5:['j','k','l'],6:['m','n','o'],7:['p','q','r','s'],8:['t','u','v'],9:['w','x','y','z']};constletterCombinations=function(digits){const result =[];functionbacktrack(prefix, next){// 发现没有字母需要输入时，就可以返回了if(next.length ===0){
      result.push(prefix);}else{const digit = next[0];const letters = map[digit];// 获取对应的各个字母for(let i =0; i < letters.length; i++){backtrack(prefix + letters[i], next.substr(1));}}}if(digits.length !==0){backtrack('', digits);}return result;};

复杂度分析

• 时间复杂度： O(3^m * 4^n)O(3m∗4n)
• 空间复杂度： O(3^m * 4^n)O(3m∗4n)

实现数组的全排列和单词搜索

实现数组的全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例

给定 numbs = [1,2,3];

返回
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

方法一 回溯法

思路

回溯法通常是构造一颗生成树，生成树排列法的核心思想为： 遍历需要全排列的数组，不断选择元素，将不同的数字生成一颗树，如果数组中待选择的结点数为 0，则完成一种全排列。

详解

从上面的思路中，我们可以抽象出全排列函数的步骤：

1. 遍历需要全排列的数组，取出不同位置的数字，创建以对应位置数字为根节点的树。

2. 遍历剩下的数组，选出一个数字，将该数字挂在生成的树上。

3. 重复第二步操作直到剩余数字数组的长度为0，表明完成了全排列，将生成的树存入排序结果数组中。

举个例子：输入数组为 [1, 2, 3]，首先选择 1 为根节点，剩余数组为 [2, 3]，继续选择 2 作为下一个结点，剩余数组为 [ 3 ]，那么选择 3 为最后一个结点，那么 [1, 2, 3] 组成一种全排列情况。 我们回溯到第二步剩余数组，选择 3 为第二个结点，那么剩余数组为 [ 2 ]，选择后完成 [1, 3, 2] 这种全排列情况。后续依次固定 2，3 为根结点，列出所有可能。

从上述内容中可以看出，生成初始树后就是一个 截取数组 -> 设置节点，继续 截取节点 -> 设置节点 的递归过程了。那么我们是否可以将第一步的操作合并到我们的递归函数中呢？

既然我们递归的操作是截取数字，并将对应的数字与目标树结合。那么我们可以将第一步看为数字和空树结合。

那么我们递归函数的参数就确定为：

• 剩余的数组
• 现有的顺序树

递归函数的逻辑也可以收敛为：

1. 遍历需要全排列的数组，将不同位置的数字与目前树结合起来
2. 重复该操作直到需要全排列的数组长度为 0，即表明完成了全排列。

代码

constpermute=function(numbs){const allSortResult =[];// 设置结果数组functionrecursion(restArr, tempResult){for(let index =0; index < restArr.length; index++){// 获取不同位置的数字const insertNumb = restArr[index];// 将不同位置的数字与现有的顺序树相结合const nextTempResult =[...tempResult, insertNumb];/**
       * 判断传入的数组长度
       * 大于1:
       * 继续递归，参数分别为：
       *  1. 除去当前数字外的数组
       *  2. 新生成的树
       * 等于1(不会出现小于1的情况):
       *  表明已经结合到了最后一个节点，将生成的顺序树推送到结果数组中
       */if(restArr.length >1){recursion(
          restArr.filter(resetNumb=> resetNumb !== insertNumb),
          nextTempResult
        );}else{
        allSortResult.push(nextTempResult);}}}// 调用递归方法，开始生成顺序树recursion(numbs,[]);// 返回全排列结果return allSortResult;};

复杂度分析

• 时间复杂度：O(n^2)O(n2)
• 空间复杂度：O(n^2)O(n2)

方法二 插值排序法

思路

插值排列法的核心思想为： 遍历需要全排列的数组，将不同位置的数字抽离出来，插入到剩余数组的不同位置，即可得到该数字与另一个数组的全排列结果。 将一个固定的数字，插入到另一个数组的全排列结果的不同位置， 遍历需要全排列的数组，将不同的数字连接到不同的树上 继续全排列剩下的数组与生成的树，当剩余数组长度为0时，表明完成了全排列。

详解

从上面的思路中，我们可以抽象出插值排序全排列方法的具体实现：

首先处理特殊情况。如果传入排列的数组长度为1，直接返回该数组。否则进行下面的全排列方法

  1. 截取传入数组的第 1 位数字，将剩余数组传入获取全排列方法函数，获取剩余数字的全排列结果

  2. 遍历剩余数字的全排列结果数组并取出各个结果

  3. 使用循环将截取的数字插入到不同结果(数组)的不同位置，生成新的全排列结果并保存

  4. 返回全排列结果数组

代码

constpermute=function(numbs){// 设定保存结果变量const result =[];// 如果长度为1，只有一种排列，直接返回if(numbs.length ===1){return[numbs];}else{// 长度大于1，获取除第一个数字外的数组的全排列结果const allSortList =permute(numbs.slice(1));// 遍历剩余数字的全排列结果数组for(let sortIndex =0; sortIndex < allSortList.length; sortIndex++){// 取出不同的全排列结果const currentSort = allSortList[sortIndex];// 将第一个数字插入到不同的位置来生成新的结果，并保存for(let index =0; index <= currentSort.length; index++){const tempSort =[...currentSort];
        tempSort.splice(index,0, numbs[0]);
        result.push(tempSort);}}// 返回全排列结果数组return result;}};

复杂度分析：

• 时间复杂度：O(n^3)O(n3) 时间复杂度由全排列函数 permute 提供。单个全排列函数中存在两层循环嵌套，因此单次调用的时间复杂度为 O(n^2)O(n2) 当 numbs 长度为 nn 到 2 时调用全排列函数，即调用 (n-2)(n−2)次 n^2(n-2) = n^3 - 2n^2n2(n−2)=n3−2n2; 当 nn 趋近于无限大时，nn 可以忽略，因此时间复杂度为 O(n^3)O(n3)
• 空间复杂度：O(n^3)O(n3)， 在循环体内使用4个变量，空间复杂度为 O(4*n^3)O(4∗n3) ，当 nn 趋近于无限大，忽略系数，即为 O(n^3)O(n3)

单词搜索

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 `true`.
给定 word = "SEE", 返回 `true`.
给定 word = "ABCB", 返回 `false`.

方法 回溯算法

思路

题目给的要求水平相邻或垂直相邻的单元格，这与回溯的思想非常相似，简单来说，上下左右都去走一遍，发现不符合要求立即返回。

以题目的示例为例子，从 A 开始，放四个方向试探，如果不匹配，立即换方向

详解

1. 从起点开始，枚举所有的可能性，递归搜索
2. 如果当前字符串匹配，再考虑上下左右 4 个方向，当发现超出边界或者不匹配时，立即结束当前方向的搜索

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */constexist=function(board, word){const m = board.length;const n = board[0].length;for(let i =0; i < m; i++){for(let j =0; j < n; j++){if(wordSearch(i, j,0)){returntrue;}}}functionwordSearch(i, j, k){// 超出边界或者不匹配时，返回 falseif(i <0|| j <0|| i >= m || j >= n || word[k]!== board[i][j]){returnfalse;}// 找到最后一个字符，返回 true，为递归的终止条件if(k === word.length -1){returntrue;}// 先占位const temp = board[i][j];
    board[i][j]='-';// 往四个方向递归搜索，有一个方向匹配就可以了const res =wordSearch(i +1, j, k +1)||wordSearch(i -1, j, k +1)||wordSearch(i, j +1, k +1)||wordSearch(i, j -1, k +1);// 四个方向搜索完了释放
    board[i][j]= temp;return res;}returnfalse;};

复杂度分析

• 时间复杂度： O((mn)^2)O((m∗n)2)mm 和 nn 分别是矩阵的行数和列数。 每个递归函数 wordSearch 的调用次数为 m * nm∗n，并且调用了4个递归函数，复杂度为 O(4 * m * n)O(4∗m∗n) 在 for 循环下，时间复杂度为 O(m * n)O(m∗n)。 因此总的时间复杂度为 O(4 (m * n)^2) = O((mn)^2)O(4(m∗n)2)=O((m∗n)2)
• 空间复杂度： O(mn)O(m∗n)每个递归函数的递归深度为 m * nm∗n,* 空间复杂度为 O(m * n)O(m∗n)，一共调用了4个，因此总的复杂度为 O(4 * m * n) = O(m * n)O(4∗m∗n)=O(m∗n)

👉练习打卡