AES加密

加密算法根据加解密方法分为以下两种类型
对称加密：
加密(encryption)与解密(decryption)过程用的是同样的密钥(secret key)。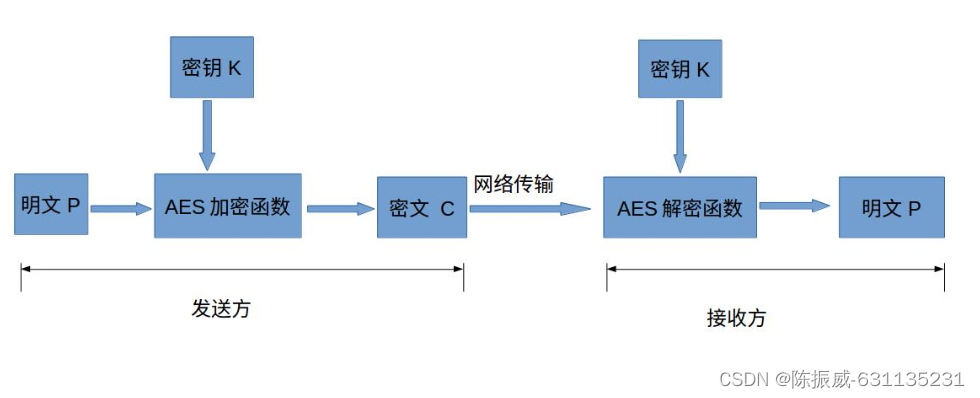

对称加密通常使用的是相对较小的密钥，一般小于256 bit。因为密钥越大，加密越强，但加密与解密的过程越慢。

对称加密的优缺点
缺点是：密钥的管理与分配，换句话说，如何把密钥发送到需要解密你的消息的人的手里是一个问题。在发送密钥的过程中，密钥有很大的风险会被黑客们拦截。现实中通常的做法是将对称加密的密钥进行非对称加密，然后传送给需要它的人。
优点是：对称加密，加密速度非常快，适合经常发送数据的场合。缺点是密钥的传输比较麻烦：

非对称加密（Asymmetric Cryptography）

非对称加密为数据的加密与解密提供了一个非常安全的方法，它使用了一对密钥，公钥(public key)和私钥(private key)。私钥只能由一方安全保管，不能外泄，而公钥则可以发给任何请求它的人。非对称加密使用这对密钥中的一个进行加密，而解密则需要另一个密钥。

非对称算法，加密解密的速度比较慢，适合偶尔发送数据的场合。优点是密钥传输方便。常见的非对称加密算法为RSA、ECC和EIGamal

AES
高级加密标准（英语：Advanced Encryption Standard，缩写：AES），在密码学中又称Rijndael加密法，是美国联邦政府采用的一种区块加密标准。这个标准用来替代原先的DES，已经被多方分析且广为全世界所使用。经过五年的甄选流程，高级加密标准由美国国家标准与技术研究院（NIST）于2001年11月26日发布于FIPS PUB 197，并在2002年5月26日成为有效的标准。2006年，高级加密标准已然成为对称密钥加密中最流行的算法之一。

AES属于对称加密算法；加密、解密使用相同的密钥，AES加解密过程如下图所示：

下面简单介绍下各个部分的作用与意义：

明文P

    没有经过加密的数据。

密钥K

    密钥是用来加密明文的密码，在对称加密算法中，加密与解密的密钥是相同的。

    密钥为接收方与发送方协商产生，但不可以直接在网络上传输，否则会导致密钥泄漏，通常是通过非对称加密算法加密密钥，然后再通过网络传输给对方，或者直接面对面商量密钥。

    密钥是绝对不可以泄漏的，否则会被攻击者还原密文，窃取机密数据。

    AES支持三种长度的密钥：**128位，192位，256位**
     平时大家所说的AES128，AES192，AES256，实际上就是指的AES算法对不同长度密钥的使用。 1个英文字母 

AES加密函数

    设AES加密函数为E，则 C = E(K, P),其中P为明文，K为密钥，C为密文。也就是说，把明文P和密钥K作为加密函数的参数输入，则加密函数E会输出密文C。

密文C

    经加密函数处理后的数据

AES解密函数

    设AES解密函数为D，则 P = D(K, C),其中C为密文，K为密钥，P为明文。也就是说，把密文C和密钥K作为解密函数的参数输入，则解密函数会输出明文P。

分组加密

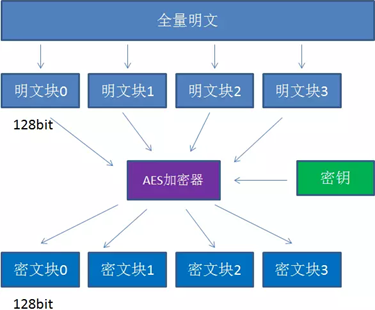
    AES算法在对明文加密的时候，并不是把整个明文一股脑加密成一整段密文，而是把明文拆分成一个个独立的明文块，每一个明文块长度128bit。
     这些明文块经过AES加密器的复杂处理，生成一个个独立的密文块，这些密文块拼接在一起，就是最终的AES加密结果 ，如下图所示

明文填充

     假如一段明文长度是192bit，如果按每128bit一个明文块来拆分的话，第二个明文块只有64bit，不足128bit。这时候怎么办呢？就需要对明文块进行**填充**（Padding）

    填充有六种：NoPadding, PKCS#5, PKCS#7, ISO 10126, ANSI X9.23和ZerosPadding 

需要注意，如果加密使用了某种填充方式，解密也需要使用相同的填充方式

NoPadding

    顾名思义，就是不填充。缺点就是只能加密长为128bits倍数的信息，一般不会使用

PKCS#7 & PKCS#5

    缺几个字节就填几个缺的字节数。

    如果明文块少于16个字节（128bit），在明文块末尾补足相应数量的字符，且每个字节的值等于缺少的字符数。
     比如明文：{1,2,3,4,5,a,b,c,d,e},缺少6个字节，则补全为{1,2,3,4,5,a,b,c,d,e,6,6,6,6,6,6}

ZerosPadding

    全部填充

0x00

，无论缺多少全部填充

0x00

ISO 10126

    最后一个字节是填充的字节数（包括最后一字节），其他全部填随机数

ANSI X9.23

    跟ISO 10126很像，只不过ANSI X9.23其他字节填的都是0而不是随机数

AES的基本结构

    AES为分组密码，分组密码也就是把明文分成一组一组的，每组长度相等，每次加密一组数据，直到加密完整个明文。在**AES标准规范中，分组长度只能是128位**，也就是说，每个分组为16个字节（每个字节8位）。密钥的长度可以使用128位、192位或256位。密钥的长度不同，推荐加密轮数也不同，如下表所示：

AES密钥长度（32位比特字)分组长度(32位比特字)加密轮数AES-1284410AES-1926412AES-2568414

    这里实现的是AES-128，也就是密钥的长度为128位，加密轮数为10轮。
     上面说到，AES的加密公式为C = E(K,P)，在加密函数E中，会执行一个轮函数，并且执行10次这个轮函数，这个轮函数的前9次执行的操作是一样的，只有第10次有所不同。也就是说，一个明文分组会被加密10轮。AES的核心就是实现一轮中的所有操作。

    AES的处理单位是字节，128位的输入明文分组P和输入密钥K都被分成16个字节，分别记为P = P0 P1 … P15 和 K = K0 K1 … K15。如，明文分组为P = abcdefghijklmnop,其中的字符a对应P0，p对应P15。一般地，明文分组用字节为单位的正方形矩阵描述，称为状态矩阵。在算法的每一轮中，状态矩阵的内容不断发生变化，最后的结果作为密文输出。该矩阵中字节的排列顺序为从上到下、从左至右依次排列，如下图所示：

现在假设明文分组P为"abcdefghijklmnop"，则对应上面生成的状态矩阵图如下：

上图中，0x61为字符a的十六进制表示。可以看到，明文经过AES加密后，已经面目全非。

    类似地，128位密钥也是用字节为单位的矩阵表示，矩阵的每一列被称为1个32位比特字。通过**密钥编排函数该密钥矩阵被扩展成一个44个字**组成的序列W[0],W[1], … ,W[43],该序列的前4个元素W[0],W[1],W[2],W[3]是原始密钥，用于加密运算中的初始密钥加（下面介绍）;后面40个字分为10组，每组4个字（128比特）分别用于10轮加密运算中的轮密钥加，如下图所示：

    上图中，设K = “abcdefghijklmnop”，则K0 = a, K15 = p, W[0] = K0 K1 K2 K3 = “abcd”。

    AES的整体结构如下图所示，其中的W[0,3]是指W[0]、W[1]、W[2]和W[3]串联组成的128位密钥。**加密的第1轮到第9轮的轮函数一样，包括4个操作：字节代换、行位移、列混合和轮密钥加。最后一轮迭代不执行列混合**。另外，在第一轮迭代之前，先将明文和原始密钥进行一次异或加密操作。

    上图也展示了AES解密过程，解密过程仍为10轮，每一轮的操作是加密操作的逆操作。由于AES的4个轮操作都是可逆的，因此，解密操作的一轮就是顺序执行逆行移位、逆字节代换、轮密钥加和逆列混合。同加密操作类似，最后一轮不执行逆列混合，在第1轮解密之前，要执行1次密钥加操作。

下面分别介绍AES中一轮的4个操作阶段，这4分操作阶段使输入位得到充分的混淆。

一、字节代换

1.字节代换操作

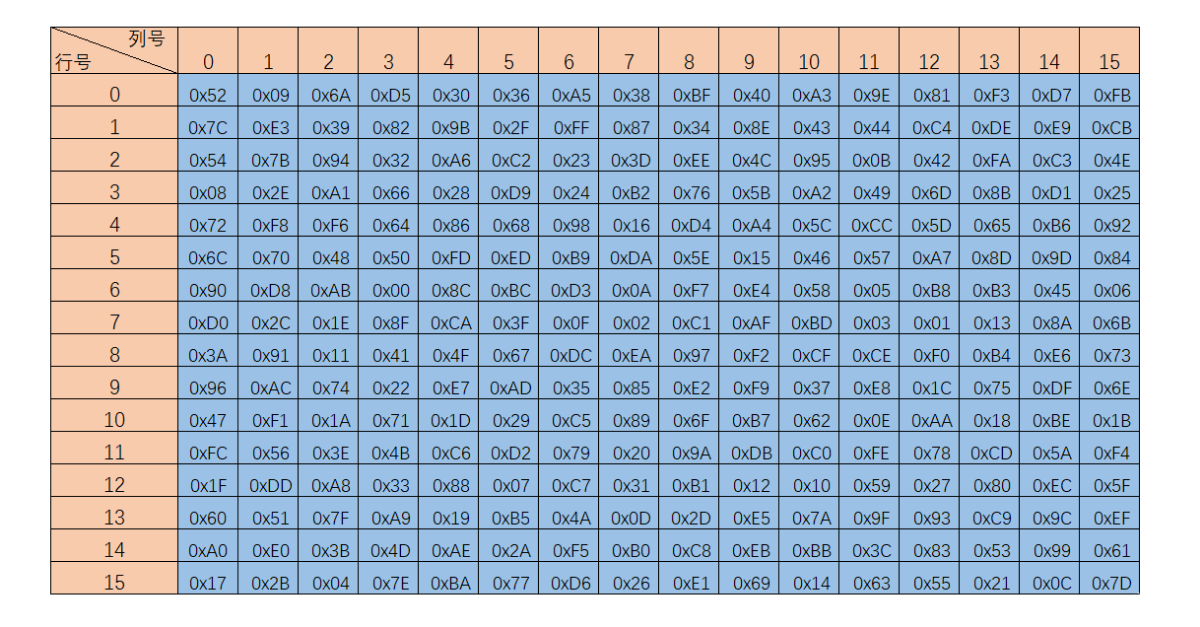
AES的字节代换其实就是一个简单的查表操作。AES定义了一个S盒和一个逆S盒。
AES的S盒：

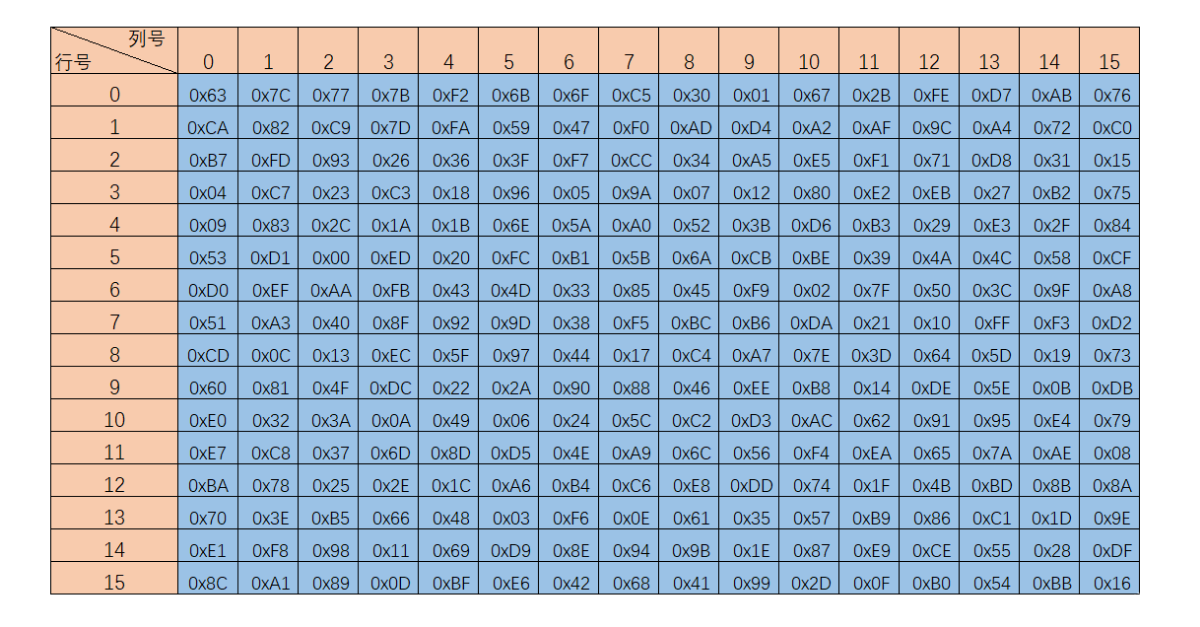
状态矩阵中的元素按照下面的方式映射为一个新的字节：把该字节的高4位作为行值，低4位作为列值，取出S盒或者逆S盒中对应的行的元素作为输出。例如，加密时，输出的字节S1为0x12,则查S盒的第0x01行和0x02列，得到值0xc9,然后替换S1原有的0x12为0xc9。状态矩阵经字节代换后的图如下：

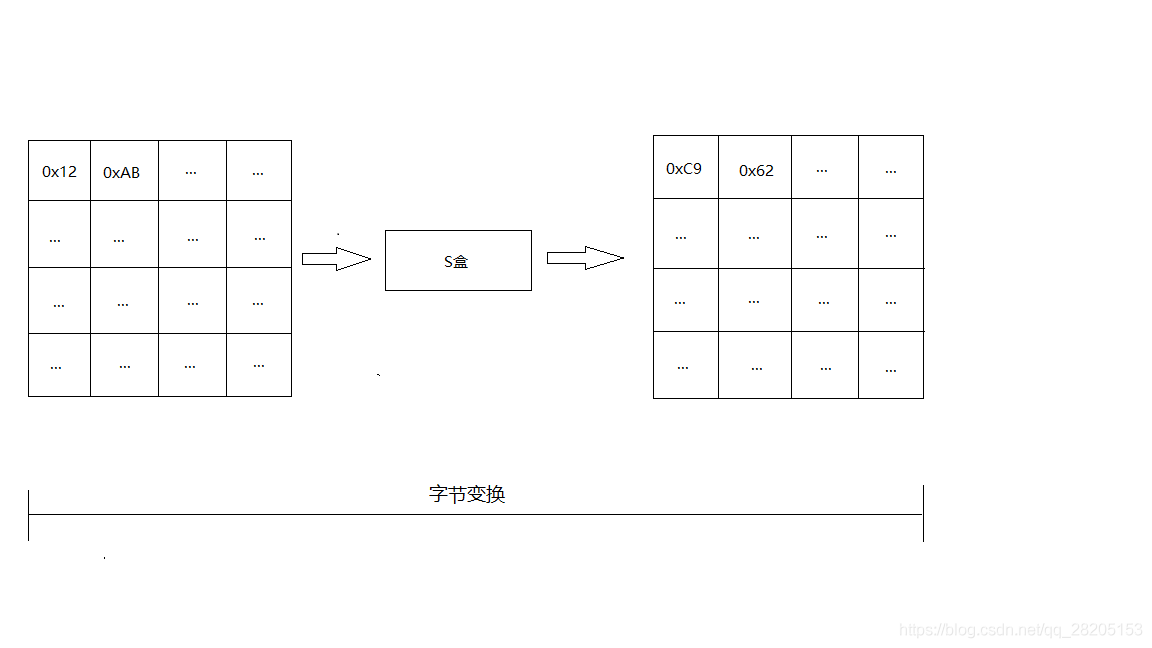
2.字节代换逆操作

逆字节代换也就是查逆S盒来变换，逆S盒如下：

二、行移位

1.行移位操作

行移位是一个简单的左循环移位操作。当密钥长度为128比特时，状态矩阵的第0行左移0字节，第1行左移1字节，第2行左移2字节，第3行左移3字节，如下图所示：

2.行移位的逆变换

行移位的逆变换是将状态矩阵中的每一行执行相反的移位操作，例如AES-128中，状态矩阵的第0行右移0字节，第1行右移1字节，第2行右移2字节，第3行右移3字节。

三、列混合

1.列混合操作

列混合变换是通过矩阵相乘来实现的，经行移位后的状态矩阵与固定的矩阵相乘，得到混淆后的状态矩阵，如下图的公式所示：

状态矩阵中的第j列(0 ≤j≤3)的列混合可以表示为下图所示：

其中，矩阵元素的乘法和加法都是定义在基于GF(2^8)上的二元运算,并不是通常意义上的乘法和加法。这里涉及到一些信息安全上的数学知识，不过不懂这些知识也行。其实这种二元运算的加法等价于两个字节的异或，乘法则复杂一点。对于一个8位的二进制数来说，使用域上的乘法乘以(00000010)等价于左移1位(低位补0)后，再根据情况同(00011011)进行异或运算，设S1 = (a7 a6 a5 a4 a3 a2 a1 a0)，刚0x02 * S1如下图所示：

————————————————
版权声明：本文为CSDN博主「TimeShatter」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_28205153/article/details/55798628

也就是说，如果a7为1，则进行异或运算，否则不进行。
类似地，乘以(00000100)可以拆分成两次乘以(00000010)的运算：

乘以(0000 0011)可以拆分成先分别乘以(0000 0001)和(0000 0010)，再将两个乘积异或：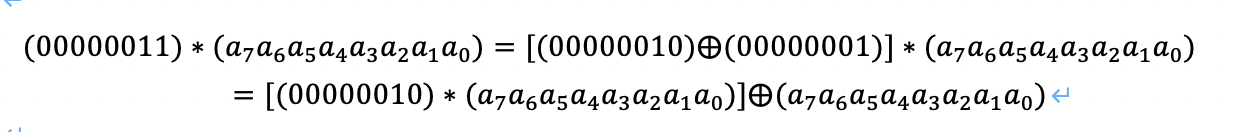

因此，我们只需要实现乘以2的函数，其他数值的乘法都可以通过组合来实现。
下面举个具体的例子,输入的状态矩阵如下：

C9E5FD2B7AF2786E639C2667B0A782E5

下面，进行列混合运算：
以第一列的运算为例：

其它列的计算就不列举了，列混合后生成的新状态矩阵如下：

D4E7CD662802E5BBBEC6D6BF220FDFA5

2.列混合逆运算

逆向列混合变换可由下图的矩阵乘法定义：

四、轮密钥加

轮密钥加是将128位轮密钥Ki同状态矩阵中的数据进行逐位异或操作，如下图所示。其中，密钥Ki中每个字W[4i],W[4i+1],W[4i+2],W[4i+3]为32位比特字，包含4个字节，他们的生成算法下面在下面介绍。轮密钥加过程可以看成是字逐位异或的结果，也可以看成字节级别或者位级别的操作。也就是说，可以看成S0 S1 S2 S3 组成的32位字与W[4i]的异或运算。

轮密钥加的逆运算同正向的轮密钥加运算完全一致，这是因为异或的逆操作是其自身。轮密钥加非常简单，但却能够影响S数组中的每一位。

密钥扩展

AES首先将初始密钥输入到一个44的状态矩阵中，如下图所示

这个44矩阵的每一列的4个字节组成一个字，矩阵4列的4个字依次命名为W[0]、W[1]、W[2]和W[3]，它们构成一个以字为单位的数组W。例如，设密钥K为"abcdefghijklmnop",则K0 = ‘a’,K1 = ‘b’, K2 = ‘c’,K3 = ‘d’,W[0] = “abcd”。
接着，对W数组扩充40个新列，构成总共44列的扩展密钥数组。新列以如下的递归方式产生：
1.如果i不是4的倍数，那么第i列由如下等式确定：
W[i]=W[i-4]⨁W[i-1]
2.如果i是4的倍数，那么第i列由如下等式确定：
W[i]=W[i-4]⨁T(W[i-1])
其中，T是一个有点复杂的函数。
函数T由3部分组成：字循环、字节代换和轮常量异或，这3部分的作用分别如下。
a.字循环：将1个字中的4个字节循环左移1个字节。即将输入字[b0, b1, b2, b3]变换成[b1,b2,b3,b0]。
b.字节代换：对字循环的结果使用S盒进行字节代换。
c.轮常量异或：将前两步的结果同轮常量Rcon[j]进行异或，其中j表示轮数。
轮常量Rcon[j]是一个字，其值见下表。

j12345Rcon[j]01 00 00 0002 00 00 0004 00 00 0008 00 00 0010 00 00 00j678910Rcon[j]20 00 00 0040 00 00 0080 00 00 001B 00 00 0036 00 00 00

下面举个例子：
设初始的128位密钥为：
3C A1 0B 21 57 F0 19 16 90 2E 13 80 AC C1 07 BD
那么4个初始值为：
W[0] = 3C

ES解密

在文章开始的图中，有AES解密的流程图，可以对应那个流程图来进行解密。下面介绍的是另一种等价的解密模式，流程图如下图所示。这种等价的解密模式使得解密过程各个变换的使用顺序同加密过程的顺序一致，只是用逆变换取代原来的变换。

A1 0B 21
W[1] = 57 F0 19 16
W[2] = 90 2E 13 80
W[3] = AC C1 07 BD
下面求扩展的第1轮的子密钥(W[4],W[5],W[6],W[7])。
由于4是4的倍数，所以：
W[4] = W[0] ⨁ T(W[3])
T(W[3])的计算步骤如下：

循环地将W[3]的元素移位：AC C1 07 BD变成C1 07 BD AC;
将 C1 07 BD AC 作为S盒的输入，输出为78 C5 7A 91;
将78 C5 7A 91与第一轮轮常量Rcon[1]进行异或运算，将得到79 C5 7A 91，因此，T(W[3])=79 C5 7A 91，故
W[4] = 3C A1 0B 21 ⨁ 79 C5 7A 91 = 45 64 71 B0
其余的3个子密钥段的计算如下：
W[5] = W[1] ⨁ W[4] = 57 F0 19 16 ⨁ 45 64 71 B0 = 12 94 68 A6
W[6] = W[2] ⨁ W[5] =90 2E 13 80 ⨁ 12 94 68 A6 = 82 BA 7B 26
W[7] = W[3] ⨁ W[6] = AC C1 07 BD ⨁ 82 BA 7B 26 = 2E 7B 7C 9B
所以，第一轮的密钥为 45 64 71 B0 12 94 68 A6 82 BA 7B 26 2E 7B 7C 9B。

AES解密

在文章开始的图中，有AES解密的流程图，可以对应那个流程图来进行解密。下面介绍的是另一种等价的解密模式，流程图如下图所示。这种等价的解密模式使得解密过程各个变换的使用顺序同加密过程的顺序一致，只是用逆变换取代原来的变换。

分组加密五种加密模式

    分组密码有五种工作体制：1.电码本模式（Electronic Codebook Book (ECB)）；2.密码分组链接模式（Cipher Block Chaining (CBC)）；3.计算器模式（Counter (CTR)）；4.密码反馈模式（Cipher FeedBack (CFB)）；5.输出反馈模式（Output FeedBack (OFB)）。

  在密码学中，分组密码操作模式是使用分组密码来提供诸如机密性或真实性的信息服务的算法。基于分组的对称密码算法比如DES/AES算法只是描述如何根据秘钥对一段固定长度（分组块）的数据进行加密，对于比较长的数据，分组密码工作模式描述了如何重复应用某种算法加密分组操作来安全地转换大于块的数据量。
  简单的说就是，AES算法描述怎么加密一个数据块，分组密码工作模式决定了如何重复加密比较长的多个数据块

ECB

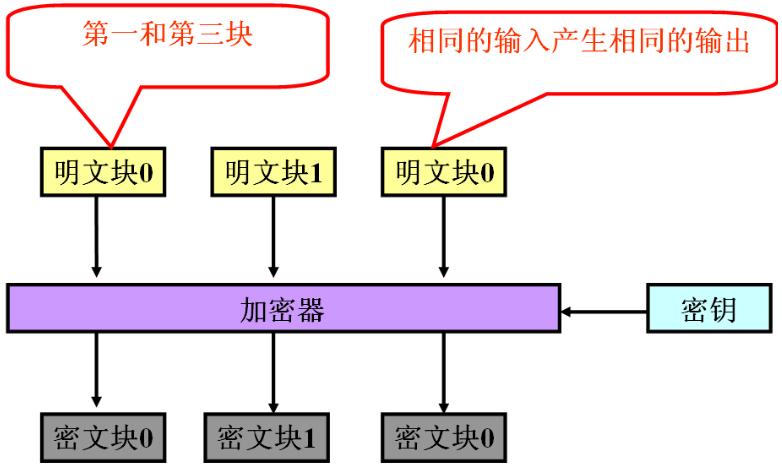
  ECB(Electronic Codebook, 电子密码本)模式是最简单的加密模式，明文消息被分成固定大小的块（分组），并且每个块被单独加密。
  每个块的加密和解密都是独立的，且使用相同的方法进行加密，所以可以进行并行计算，但是这种方法一旦有一个块被破解，使用相同的方法可以解密所有的明文数据，安全性比较差。
  适用于数据较少的情形，加密前需要把明文数据填充到块大小的整倍数。

优点:

1.简单；

2.有利于并行计算；

3.误差不会被传送；

缺点:

1.不能隐藏明文的模式；

2.可能对明文进行主动攻击；

CBC

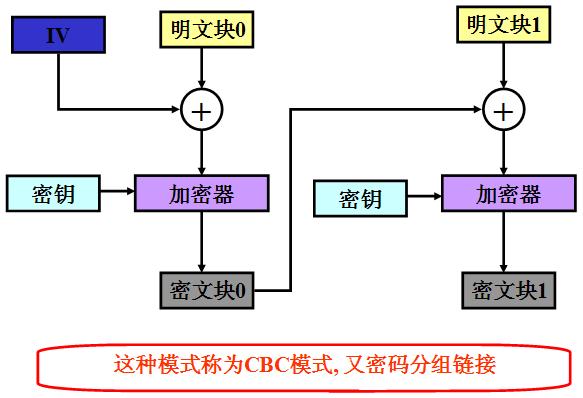
  CBC(Cipher Block Chaining, 密码块链)模式中每一个分组要先和前一个分组加密后的数据进行XOR异或操作，然后再进行加密。
  这样每个密文块依赖该块之前的所有明文块，为了保持每条消息都具有唯一性，第一个数据块进行加密之前需要用初始化向量IV进行异或操作。
  CBC模式是一种最常用的加密模式，它主要缺点是加密是连续的，不能并行处理，并且与ECB一样消息块必须填充到块大小的整倍数。

优点：

1.不容易主动攻击,安全性好于ECB,适合传输长度长的报文,是SSL、IPSec的标准。

缺点：

1.不利于并行计算；

2.误差传递；

3.需要初始化向量IV

CFB

  CFB(Cipher Feedback, 密码反馈)模式和CBC模式比较相似，前一个分组的密文加密后和当前分组的明文XOR异或操作生成当前分组的密文。CFB模式的解密和CBC模式的加密在流程上其实是非常相似的

优点：

1.隐藏了明文模式;

2.分组密码转化为流模式;

3.可以及时加密传送小于分组的数据;

缺点:

1.不利于并行计算;

2.误差传送：一个明文单元损坏影响多个单元;

3.唯一的IV;

OFB

  OFB(Output Feedback, 输出反馈)模式将分组密码转换为同步流密码，也就是说可以根据明文长度先独立生成相应长度的流密码。通过流程图可以看出，OFB和CFB非常相似，CFB是前一个分组的密文加密后XOR当前分组明文，OFB是前一个分组与前一个明文块异或之前的流密码XOR当前分组明文。由于异或操作的对称性，OFB模式的解密和加密完全一样的流程。

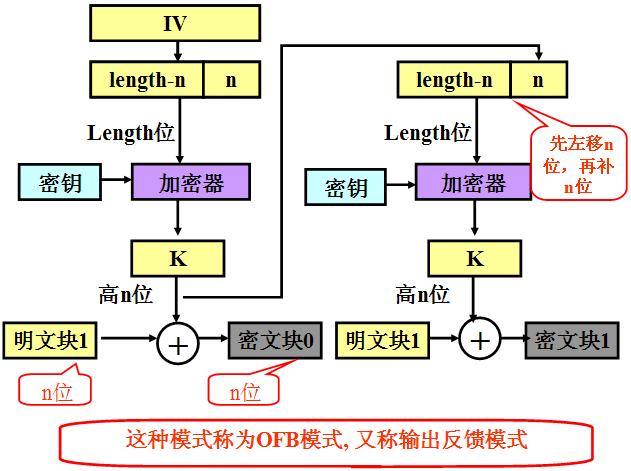
优点:

1.隐藏了明文模式;

2.分组密码转化为流模式;

3.可以及时加密传送小于分组的数据;

缺点:

1.不利于并行计算;

2.对明文的主动攻击是可能的;

3.误差传送：一个明文单元损坏影响多个单元;

</article>