现代密码学实验五：签名算法

一、实验目的

1.掌握数字签名的基本原理，理解RSA算法如何提供数字签名。

2.熟悉实验环境和加密软件CrypTool 1.4(CrypTool 2)的使用。

3.编写代码实现签名算法。

二、实验内容

1. 运行CrypTool 1.4(CrypTool 2)，使用RSA算法对消息进行签名操作，选择公钥PK=(e,N),私钥为sk=(d,N)。例如：

消息：

Out of all cryptographic primitives, the digital signature using public key cryptography is considered as very important and useful tool to achieve information security. Apart from ability to provide non-repudiation of message, the digital signature also provides message authentication and data integrity.

密钥：e = 11

N =

97837973726418359868516951718991281325771149750958732944765111213631328027493925740023000937277990315891588119835562940190113563334615471147089645563941484459898854377253031679968434226000865737244299665393453851802313775580309976978804698982229486068546397607971083305570968358870209409102684170827187712579

d =

53366167487137287201009246392177062541329718045977490697144606116526178924087595858194364147606176535940866247183034331012789216364335711534776170307604435275621882890925722486791216663911766481240927473604083681494108652553529557950472379863877351129463207267185120618342084129306558631987155442108022251891

1. 编程实现RSA/ElGamal签名算法并测试签名和验证过程。要求消息头部包含作者的姓名拼音，并通过哈希函数SHA-1得到消息摘要，对摘要进行签名，编程语言不限。

• 实验步骤

实验（1）：

1. 通过课堂与课本得知，RSA签名和实验4中的RSA算法正好相反，解密对应于签名，且解密的密钥为加密者的私钥。加密对应于验证，于是打开Cryptool2.1使用RSA解密算法生成16进制文件。如图一、二。

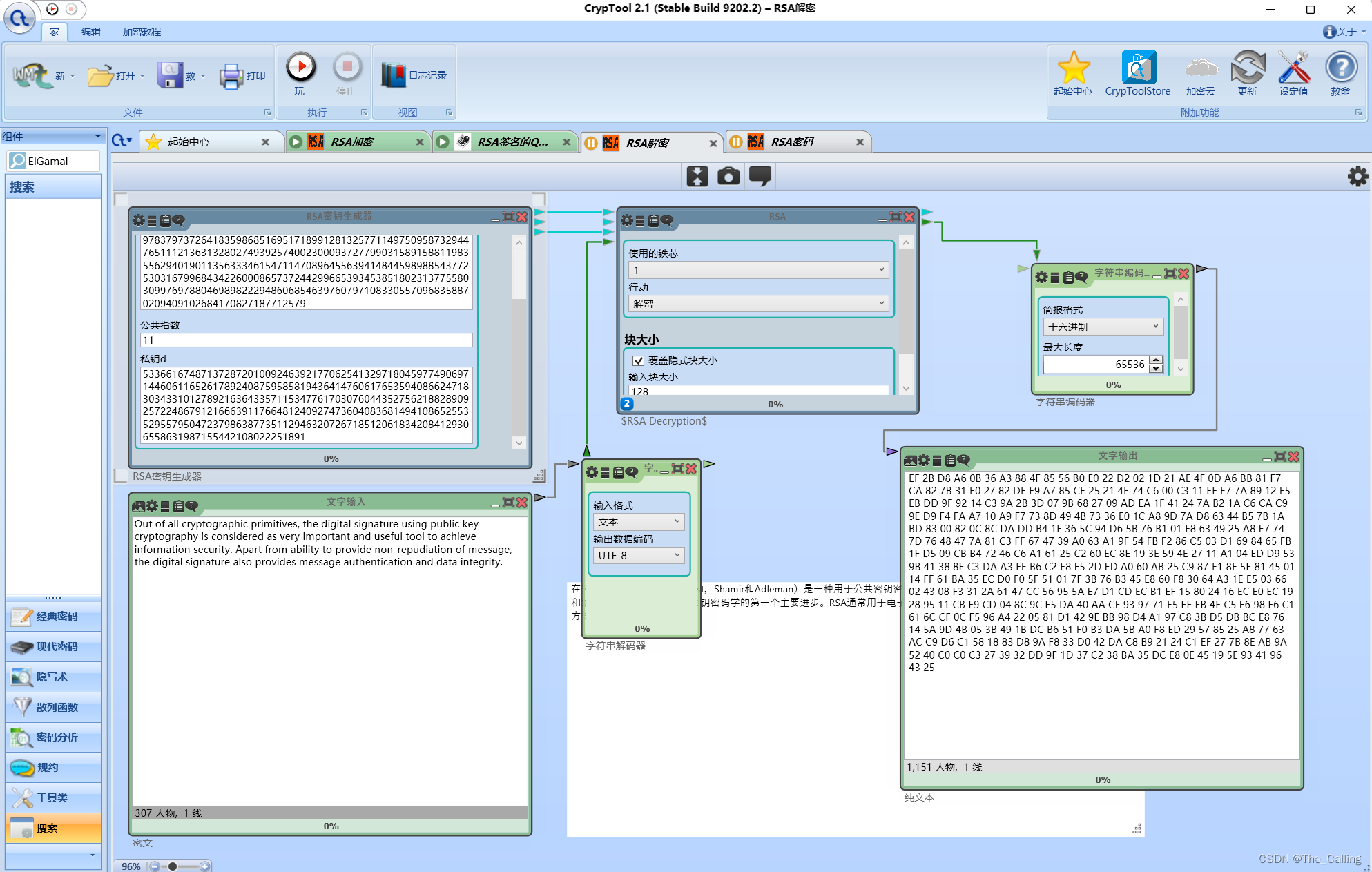
图一：签名过程

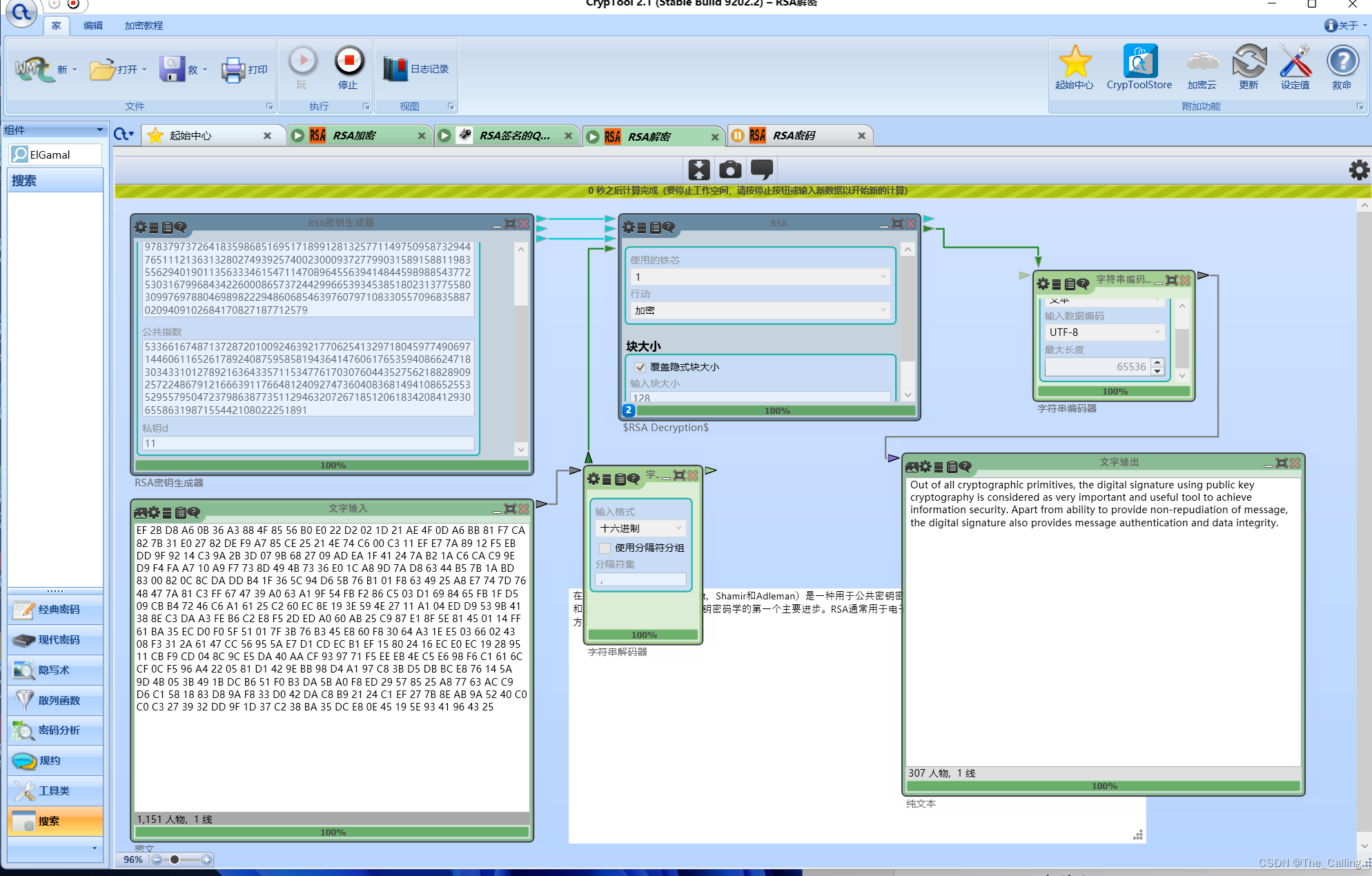
图二：验证过程

实验（2）：

1、运用python自带的库生成sha-1消息摘要（图三）：

图三：sha-1实现

2、将实验4的RSA算法实现倒置，解密对应签名，加密对应验证（如图四，五）

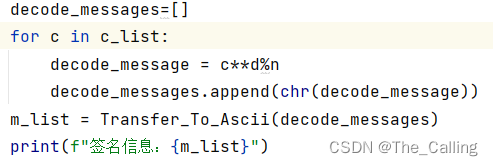
图四：解密对应签名

图五：加密对应验证

• 实验结果

实验（1）：

数字签名：

EF 2B D8 A6 0B 36 A3 88 4F 85 56 B0 E0 22 D2 02 1D 21 AE 4F 0D A6 BB 81 F7 CA 82 7B 31 E0 27 82 DE F9 A7 85 CE 25 21 4E 74 C6 00 C3 11 EF E7 7A 89 12 F5 EB DD 9F 92 14 C3 9A 2B 3D 07 9B 68 27 09 AD EA 1F 41 24 7A B2 1A C6 CA C9 9E D9 F4 FA A7 10 A9 F7 73 8D 49 4B 73 36 E0 1C A8 9D 7A D8 63 44 B5 7B 1A BD 83 00 82 0C 8C DA DD B4 1F 36 5C 94 D6 5B 76 B1 01 F8 63 49 25 A8 E7 74 7D 76 48 47 7A 81 C3 FF 67 47 39 A0 63 A1 9F 54 FB F2 86 C5 03 D1 69 84 65 FB 1F D5 09 CB B4 72 46 C6 A1 61 25 C2 60 EC 8E 19 3E 59 4E 27 11 A1 04 ED D9 53 9B 41 38 8E C3 DA A3 FE B6 C2 E8 F5 2D ED A0 60 AB 25 C9 87 E1 8F 5E 81 45 01 14 FF 61 BA 35 EC D0 F0 5F 51 01 7F 3B 76 B3 45 E8 60 F8 30 64 A3 1E E5 03 66 02 43 08 F3 31 2A 61 47 CC 56 95 5A E7 D1 CD EC B1 EF 15 80 24 16 EC E0 EC 19 28 95 11 CB F9 CD 04 8C 9C E5 DA 40 AA CF 93 97 71 F5 EE EB 4E C5 E6 98 F6 C1 61 6C CF 0C F5 96 A4 22 05 81 D1 42 9E BB 98 D4 A1 97 C8 3B D5 DB BC E8 76 14 5A 9D 4B 05 3B 49 1B DC B6 51 F0 B3 DA 5B A0 F8 ED 29 57 85 25 A8 77 63 AC C9 D6 C1 58 18 83 D8 9A F8 33 D0 42 DA C8 B9 21 24 C1 EF 27 7B 8E AB 9A 52 40 C0 C0 C3 27 39 32 DD 9F 1D 37 C2 38 BA 35 DC E8 0E 45 19 5E 93 41 96 43 25

RSA加密后生成的密文：

Out of all cryptographic primitives, the digital signature using public key cryptography is considered as very important and useful tool to achieve information security. Apart from ability to provide non-repudiation of message, the digital signature also provides message authentication and data integrity.

与原文相同，验证成功。

实验（2）：

私钥对消息摘要进行签名后，运用公钥验证签名，结果与摘要相同，验证成功！（如图六）

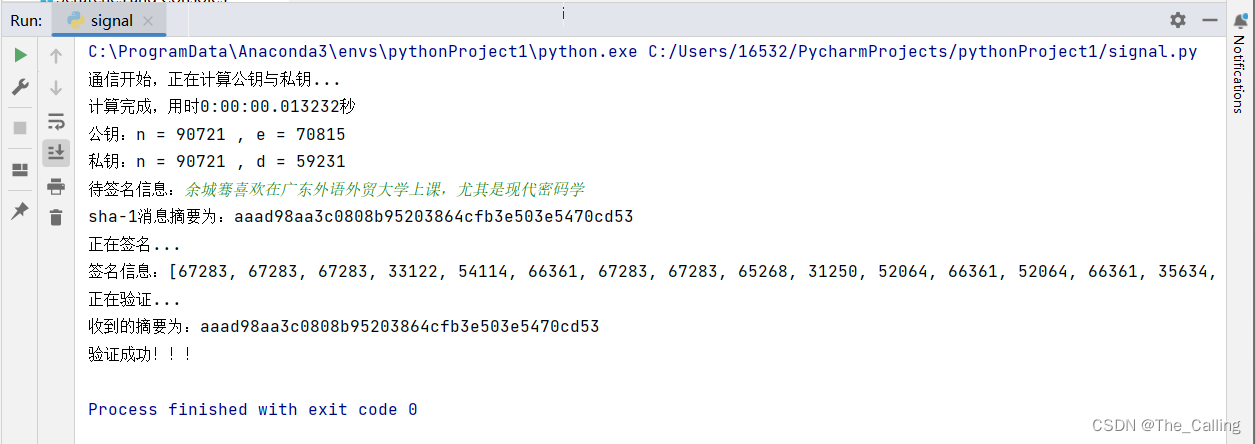
图六：运行结果

• 实验心得

本次实验的综合性较高，运用了前几课的知识，包括sha-1算法生成消息验证码，RSA算法实现不对称加密，在运用其不对称加密的性质实现数字签名，而这一切都是基于复杂的离散对数问题。Sha-1算法生成固定长度但又对明文具有强抗碰撞性，使得对摘要生成的签名长度很短都能达到较好的验证效果。

• 附录 （程序代码）

from random import randint

from datetime import datetime

import hashlib

"""判断是否是素数"""

def is_sushu(sushu):

    for i in range(2,sushu):

        if sushu % i == 0:

            return False

    return True

"""随机生成指定范围的大素数"""

def Create_Sushu():

    while True:

        sushu = randint(100,1000 )*#**下限越大，加密越安全，此处考虑计算时间，取值较小

        *if is_sushu(sushu):

            return sushu

"""计算欧拉函数"""

def Oula(sushu1 , sushu2):

    return (sushu1-1)*(sushu2-1)

"""判断是否互质"""

def Is_Huzhi(int_min,int_max):

    for i in range(2,int_min+1):

        if int_min % i == 0 and int_max % i == 0:

            return False

    return True

"""计算公钥，直接计算编程较简单，此处考虑了计算效率的优化"""

def Creat_E(oula):

    top = oula

    while True:

        i = randint(2,top)

        for e in range(i,top):

            if Is_Huzhi(e,oula):

                return e

        top = i

"""计算私钥"""

def Compute_D(oula,e):

    k = 1

    while ( k*oula+1 )% e != 0:

        k+=1

    return int((k*oula+1)/e)

"""将字符串转成ASCII"""

def Transfer_To_Ascii(messages):

    result = []

    for message in messages:

        result.append(  ord(message) )

    return result

"""将列表转化成字符串"""

def Transfer_To_String(string_list):

    string = ''.join('%s' %id for id in string_list)       *#**有数字不能直接**join .join('%s' %id for id in list1))

    *return string

if __name__ == "__main__":

    """

    p、q为大素数
    n=p*q

    oula = （p-1）* （q-1）
    e 为公钥
    d 为私钥
    """

    print("通信开始，正在计算公钥与私钥...")

    time_start = datetime.now()

    p = Create_Sushu()

    q = p

    while p ==q :

        q = Create_Sushu()

    n = p * q

    oula = Oula(p, q)

    e = Creat_E(oula)

    d = Compute_D(oula,e)

    time_end = datetime.now()

    print(f"计算完成，用时{str(time_end -time_start)}秒 ")

    print(f"公钥：n = {str(n)} , e = {str(e)}")

    print(f"私钥：n = {str(n)} , d = {str(d)}")

    m = input('待签名信息：')

    hash = hashlib.sha1(m.encode("utf-8")).hexdigest()

    c_list= Transfer_To_Ascii(hash)

    print(f"sha-1消息摘要为：{hash}")

    print("正在签名...")

    decode_messages=[]

    for c in c_list:

        decode_message = c**d%n

        decode_messages.append(chr(decode_message))

    m_list = Transfer_To_Ascii(decode_messages)

    print(f"签名信息：{m_list}")

    c_list = []

    for m in m_list:

        c = m**e%n

        c_list.append(chr(c))

    print("正在验证...")

    print(f"收到的摘要为：{Transfer_To_String(c_list)}")

    if Transfer_To_String(c_list) == hash:

        print("验证成功！！！")