从零开始学习 Java：简单易懂的入门指南之查找算法及排序算法（二十）

查找算法及排序算法

常见的七种查找算法：

1. 基本查找

​ 也叫做顺序查找

​ 说明：顺序查找适合于存储结构为数组或者链表。

基本思想：顺序查找也称为线形查找，属于无序查找算法。从数据结构线的一端开始，顺序扫描，依次将遍历到的结点与要查找的值相比较，若相等则表示查找成功；若遍历结束仍没有找到相同的，表示查找失败。

示例代码：

publicclassA01_BasicSearchDemo1{publicstaticvoidmain(String[] args){//基本查找/顺序查找//核心：//从0索引开始挨个往后查找//需求：定义一个方法利用基本查找，查询某个元素是否存在//数据如下：{131, 127, 147, 81, 103, 23, 7, 79}int[] arr ={131,127,147,81,103,23,7,79};int number =82;System.out.println(basicSearch(arr, number));}//参数：//一：数组//二：要查找的元素//返回值：//元素是否存在publicstaticbooleanbasicSearch(int[] arr,int number){//利用基本查找来查找number在数组中是否存在for(int i =0; i < arr.length; i++){if(arr[i]== number){returntrue;}}returnfalse;}}

2. 二分查找

​ 也叫做折半查找

说明：元素必须是有序的，从小到大，或者从大到小都是可以的。

如果是无序的，也可以先进行排序。但是排序之后，会改变原有数据的顺序，查找出来元素位置跟原来的元素可能是不一样的，所以排序之后再查找只能判断当前数据是否在容器当中，返回的索引无实际的意义。

基本思想：也称为是折半查找，属于有序查找算法。用给定值先与中间结点比较。比较完之后有三种情况：

• 相等说明找到了
• 要查找的数据比中间节点小说明要查找的数字在中间节点左边
• 要查找的数据比中间节点大说明要查找的数字在中间节点右边

代码示例：

packagecom.itheima.search;publicclassA02_BinarySearchDemo1{publicstaticvoidmain(String[] args){//二分查找/折半查找//核心：//每次排除一半的查找范围//需求：定义一个方法利用二分查找，查询某个元素在数组中的索引//数据如下：{7, 23, 79, 81, 103, 127, 131, 147}int[] arr ={7,23,79,81,103,127,131,147};System.out.println(binarySearch(arr,150));}publicstaticintbinarySearch(int[] arr,int number){//1.定义两个变量记录要查找的范围int min =0;int max = arr.length -1;//2.利用循环不断的去找要查找的数据while(true){if(min > max){return-1;}//3.找到min和max的中间位置int mid =(min + max)/2;//4.拿着mid指向的元素跟要查找的元素进行比较if(arr[mid]> number){//4.1 number在mid的左边//min不变，max = mid - 1；
                max = mid -1;}elseif(arr[mid]< number){//4.2 number在mid的右边//max不变，min = mid + 1;
                min = mid +1;}else{//4.3 number跟mid指向的元素一样//找到了return mid;}}}}

3. 插值查找

在介绍插值查找之前，先考虑一个问题：

​ 为什么二分查找算法一定要是折半，而不是折四分之一或者折更多呢？

其实就是因为方便，简单，但是如果我能在二分查找的基础上，让中间的mid点，尽可能靠近想要查找的元素，那不就能提高查找的效率了吗？

二分查找中查找点计算如下：

mid=(low+high)/2, 即mid=low+1/2*(high-low);

我们可以将查找的点改进为如下：

mid=low+(key-a[low])/(a[high]-a[low])*(high-low)
　　这样，让mid值的变化更靠近关键字key，这样也就间接地减少了比较次数。

基本思想：基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率。当然，差值查找也属于有序查找。

细节：对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。

代码跟二分查找类似，只要修改一下mid的计算方式即可。

4. 斐波那契查找

在介绍斐波那契查找算法之前，我们先介绍一下很它紧密相连并且大家都熟知的一个概念——黄金分割。

黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。

0.618被公认为最具有审美意义的比例数字，这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。

在数学中有一个非常有名的数学规律：斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….

（从第三个数开始，后边每一个数都是前两个数的和）。

然后我们会发现，随着斐波那契数列的递增，前后两个数的比值会越来越接近0.618，利用这个特性，我们就可以将黄金比例运用到查找技术中。

基本思想：也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。

斐波那契查找也是在二分查找的基础上进行了优化，优化中间点mid的计算方式即可

代码示例：

publicclassFeiBoSearchDemo{publicstaticint maxSize =20;publicstaticvoidmain(String[] args){int[] arr ={1,8,10,89,1000,1234};System.out.println(search(arr,1234));}publicstaticint[]getFeiBo(){int[] arr =newint[maxSize];
        arr[0]=1;
        arr[1]=1;for(int i =2; i < maxSize; i++){
            arr[i]= arr[i -1]+ arr[i -2];}return arr;}publicstaticintsearch(int[] arr,int key){int low =0;int high = arr.length -1;//表示斐波那契数分割数的下标值int index =0;int mid =0;//调用斐波那契数列int[] f =getFeiBo();//获取斐波那契分割数值的下标while(high >(f[index]-1)){
            index++;}//因为f[k]值可能大于a的长度，因此需要使用Arrays工具类，构造一个新法数组，并指向temp[],不足的部分会使用0补齐int[] temp =Arrays.copyOf(arr, f[index]);//实际需要使用arr数组的最后一个数来填充不足的部分for(int i = high +1; i < temp.length; i++){
            temp[i]= arr[high];}//使用while循环处理，找到key值while(low <= high){
            mid = low + f[index -1]-1;if(key < temp[mid]){//向数组的前面部分进行查找
                high = mid -1;/*
                  对k--进行理解
                  1.全部元素=前面的元素+后面的元素
                  2.f[k]=k[k-1]+f[k-2]
                  因为前面有k-1个元素没所以可以继续分为f[k-1]=f[k-2]+f[k-3]
                  即在f[k-1]的前面继续查找k--
                  即下次循环,mid=f[k-1-1]-1
                 */
                index--;}elseif(key > temp[mid]){//向数组的后面的部分进行查找
                low = mid +1;
                index -=2;}else{//找到了//需要确定返回的是哪个下标if(mid <= high){return mid;}else{return high;}}}return-1;}}

5. 分块查找

当数据表中的数据元素很多时，可以采用分块查找。

汲取了顺序查找和折半查找各自的优点，既有动态结构，又适于快速查找

分块查找适用于数据较多，但是数据不会发生变化的情况，如果需要一边添加一边查找，建议使用哈希查找

分块查找的过程：

1. 需要把数据分成N多小块，块与块之间不能有数据重复的交集。
2. 给每一块创建对象单独存储到数组当中
3. 查找数据的时候，先在数组查，当前数据属于哪一块
4. 再到这一块中顺序查找

代码示例：

packagecom.itheima.search;publicclassA03_BlockSearchDemo{publicstaticvoidmain(String[] args){/*
            分块查找
            核心思想：
                块内无序，块间有序
            实现步骤：
                1.创建数组blockArr存放每一个块对象的信息
                2.先查找blockArr确定要查找的数据属于哪一块
                3.再单独遍历这一块数据即可
        */int[] arr ={16,5,9,12,21,18,32,23,37,26,45,34,50,48,61,52,73,66};//创建三个块的对象Block b1 =newBlock(21,0,5);Block b2 =newBlock(45,6,11);Block b3 =newBlock(73,12,17);//定义数组用来管理三个块的对象（索引表）Block[] blockArr ={b1,b2,b3};//定义一个变量用来记录要查找的元素int number =37;//调用方法，传递索引表，数组，要查找的元素int index =getIndex(blockArr,arr,number);//打印一下System.out.println(index);}//利用分块查找的原理，查询number的索引privatestaticintgetIndex(Block[] blockArr,int[] arr,int number){//1.确定number是在那一块当中int indexBlock =findIndexBlock(blockArr, number);if(indexBlock ==-1){//表示number不在数组当中return-1;}//2.获取这一块的起始索引和结束索引   --- 30// Block b1 = new Block(21,0,5);   ----  0// Block b2 = new Block(45,6,11);  ----  1// Block b3 = new Block(73,12,17); ----  2int startIndex = blockArr[indexBlock].getStartIndex();int endIndex = blockArr[indexBlock].getEndIndex();//3.遍历for(int i = startIndex; i <= endIndex; i++){if(arr[i]== number){return i;}}return-1;}//定义一个方法，用来确定number在哪一块当中publicstaticintfindIndexBlock(Block[] blockArr,int number){//100//从0索引开始遍历blockArr，如果number小于max，那么就表示number是在这一块当中的for(int i =0; i < blockArr.length; i++){if(number <= blockArr[i].getMax()){return i;}}return-1;}}classBlock{privateint max;//最大值privateint startIndex;//起始索引privateint endIndex;//结束索引publicBlock(){}publicBlock(int max,int startIndex,int endIndex){this.max = max;this.startIndex = startIndex;this.endIndex = endIndex;}/**
     * 获取
     * @return max
     */publicintgetMax(){return max;}/**
     * 设置
     * @param max
     */publicvoidsetMax(int max){this.max = max;}/**
     * 获取
     * @return startIndex
     */publicintgetStartIndex(){return startIndex;}/**
     * 设置
     * @param startIndex
     */publicvoidsetStartIndex(int startIndex){this.startIndex = startIndex;}/**
     * 获取
     * @return endIndex
     */publicintgetEndIndex(){return endIndex;}/**
     * 设置
     * @param endIndex
     */publicvoidsetEndIndex(int endIndex){this.endIndex = endIndex;}publicStringtoString(){return"Block{max = "+ max +", startIndex = "+ startIndex +", endIndex = "+ endIndex +"}";}}

6. 哈希查找

哈希查找是分块查找的进阶版，适用于数据一边添加一边查找的情况。

一般是数组 + 链表的结合体或者是数组+链表 + 红黑树的结合体

在课程中，为了让大家方便理解，所以规定：

• 数组的0索引处存储1~100
• 数组的1索引处存储101~200
• 数组的2索引处存储201~300
• 以此类推

但是实际上，我们一般不会采取这种方式，因为这种方式容易导致一块区域添加的元素过多，导致效率偏低。

更多的是先计算出当前数据的哈希值，用哈希值跟数组的长度进行计算，计算出应存入的位置，再挂在数组的后面形成链表，如果挂的元素太多而且数组长度过长，我们也会把链表转化为红黑树，进一步提高效率。
![%8C%/img21-36-50.png)]](https://img-blog.csdnimg.cn/dcdc6edcb97f482985beae20920c2308.png)

7. 树表查找

本知识点涉及到数据结构：树。

基本思想：二叉查找树是先对待查找的数据进行生成树，确保树的左分支的值小于右分支的值，然后在就行和每个节点的父节点比较大小，查找最适合的范围。 这个算法的查找效率很高，但是如果使用这种查找方法要首先创建树。

二叉查找树（BinarySearch Tree，也叫二叉搜索树，或称二叉排序树Binary Sort Tree），具有下列性质的二叉树：

1）若任意节点左子树上所有的数据，均小于本身；

2）若任意节点右子树上所有的数据，均大于本身；

二叉查找树性质：对二叉查找树进行中序遍历，即可得到有序的数列。

基于二叉查找树进行优化，进而可以得到其他的树表查找算法，如平衡树、红黑树等高效算法。

​ 不管是二叉查找树，还是平衡二叉树，还是红黑树，查找的性能都比较高

四种排序算法：

1. 冒泡排序

冒泡排序（Bubble Sort）也是一种简单直观的排序算法。

它重复的遍历过要排序的数列，一次比较相邻的两个元素，如果他们的顺序错误就把他们交换过来。

这个算法的名字由来是因为越大的元素会经由交换慢慢"浮"到最后面。

当然，大家可以按照从大到小的方式进行排列。

1.1 算法步骤

1. 相邻的元素两两比较，大的放右边，小的放左边
2. 第一轮比较完毕之后，最大值就已经确定，第二轮可以少循环一次，后面以此类推
3. 如果数组中有n个数据，总共我们只要执行n-1轮的代码就可以

1.2 动图演示

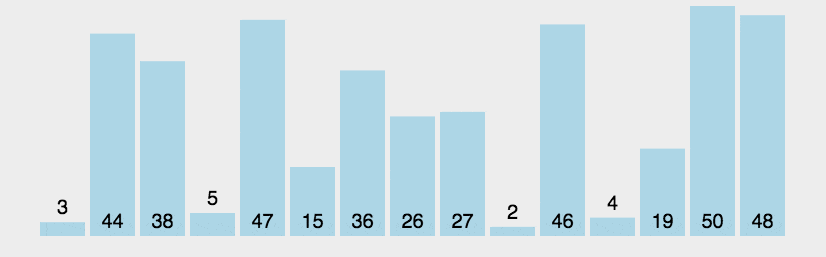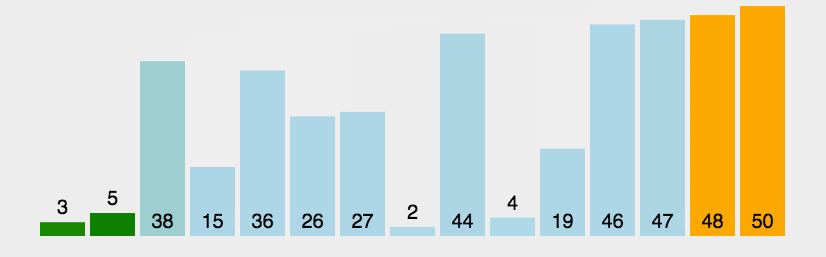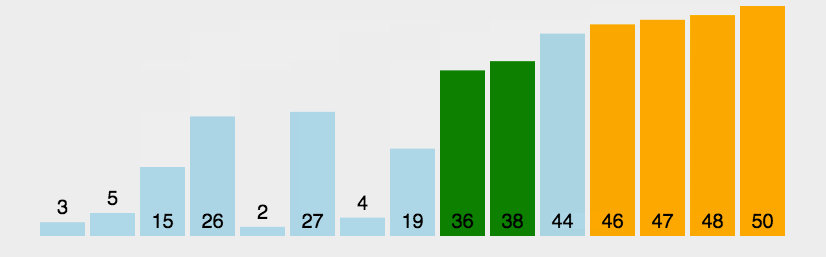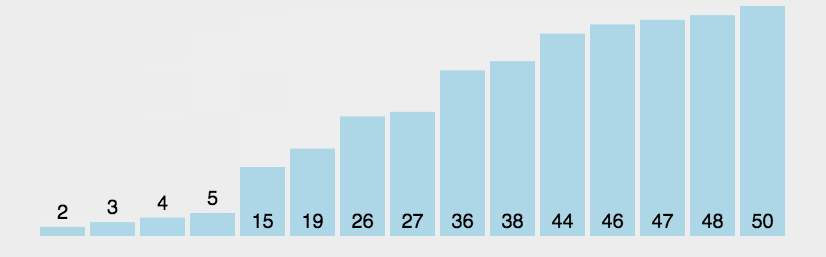
1.3 代码示例

publicclassA01_BubbleDemo{publicstaticvoidmain(String[] args){/*
            冒泡排序：
            核心思想：
            1，相邻的元素两两比较，大的放右边，小的放左边。
            2，第一轮比较完毕之后，最大值就已经确定，第二轮可以少循环一次，后面以此类推。
            3，如果数组中有n个数据，总共我们只要执行n-1轮的代码就可以。
        *///1.定义数组int[] arr ={2,4,5,3,1};//2.利用冒泡排序将数组中的数据变成 1 2 3 4 5//外循环：表示我要执行多少轮。 如果有n个数据，那么执行n - 1 轮for(int i =0; i < arr.length -1; i++){//内循环：每一轮中我如何比较数据并找到当前的最大值//-1：为了防止索引越界//-i：提高效率，每一轮执行的次数应该比上一轮少一次。for(int j =0; j < arr.length -1- i; j++){//i 依次表示数组中的每一个索引：0 1 2 3 4if(arr[j]> arr[j +1]){int temp = arr[j];
                    arr[j]= arr[j +1];
                    arr[j +1]= temp;}}}printArr(arr);}privatestaticvoidprintArr(int[] arr){//3.遍历数组for(int i =0; i < arr.length; i++){System.out.print(arr[i]+" ");}System.out.println();}}

2. 选择排序

2.1 算法步骤

1. 从0索引开始，跟后面的元素一一比较
2. 小的放前面，大的放后面
3. 第一次循环结束后，最小的数据已经确定
4. 第二次循环从1索引开始以此类推
5. 第三轮循环从2索引开始以此类推
6. 第四轮循环从3索引开始以此类推。

2.2 动图演示

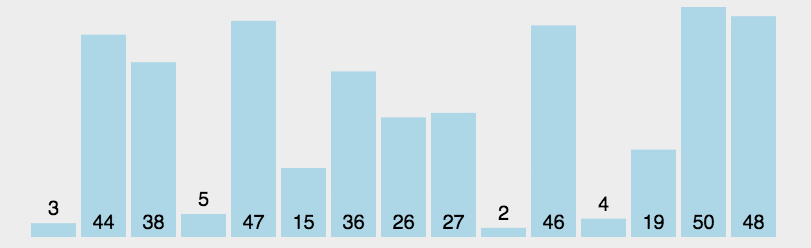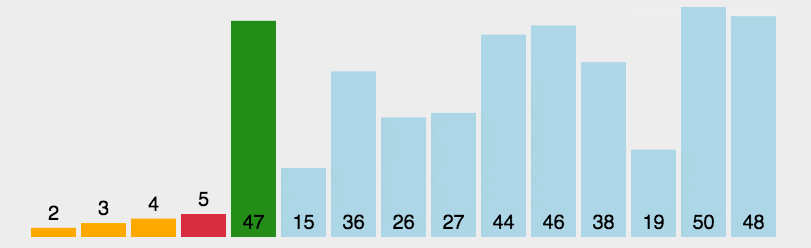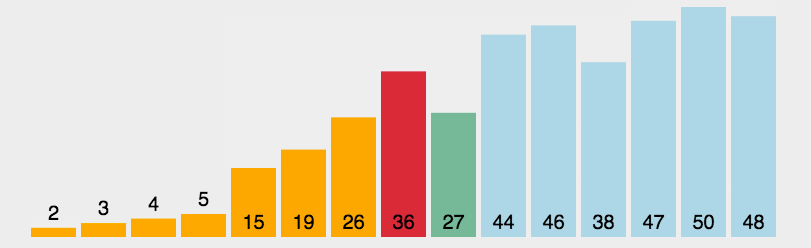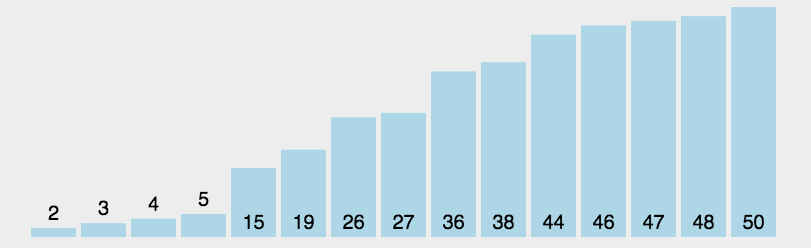
publicclassA02_SelectionDemo{publicstaticvoidmain(String[] args){/*
            选择排序：
                1，从0索引开始，跟后面的元素一一比较。
                2，小的放前面，大的放后面。
                3，第一次循环结束后，最小的数据已经确定。
                4，第二次循环从1索引开始以此类推。

         *///1.定义数组int[] arr ={2,4,5,3,1};//2.利用选择排序让数组变成 1 2 3 4 5/* //第一轮：
        //从0索引开始，跟后面的元素一一比较。
        for (int i = 0 + 1; i < arr.length; i++) {
            //拿着0索引跟后面的数据进行比较
            if(arr[0] > arr[i]){
                int temp = arr[0];
                arr[0] = arr[i];
                arr[i] = temp;
            }
        }*///最终代码：//外循环：几轮//i:表示这一轮中，我拿着哪个索引上的数据跟后面的数据进行比较并交换for(int i =0; i < arr.length -1; i++){//内循环：每一轮我要干什么事情？//拿着i跟i后面的数据进行比较交换for(int j = i +1; j < arr.length; j++){if(arr[i]> arr[j]){int temp = arr[i];
                    arr[i]= arr[j];
                    arr[j]= temp;}}}printArr(arr);}privatestaticvoidprintArr(int[] arr){//3.遍历数组for(int i =0; i < arr.length; i++){System.out.print(arr[i]+" ");}System.out.println();}}

3. 插入排序

插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴，但它的原理应该是最容易理解的了，因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法，它的工作原理是通过创建有序序列和无序序列，然后再遍历无序序列得到里面每一个数字，把每一个数字插入到有序序列中正确的位置。

插入排序在插入的时候，有优化算法，在遍历有序序列找正确位置时，可以采取二分查找

3.1 算法步骤

将0索引的元素到N索引的元素看做是有序的，把N+1索引的元素到最后一个当成是无序的。

遍历无序的数据，将遍历到的元素插入有序序列中适当的位置，如遇到相同数据，插在后面。

N的范围：0~最大索引

3.2 动图演示

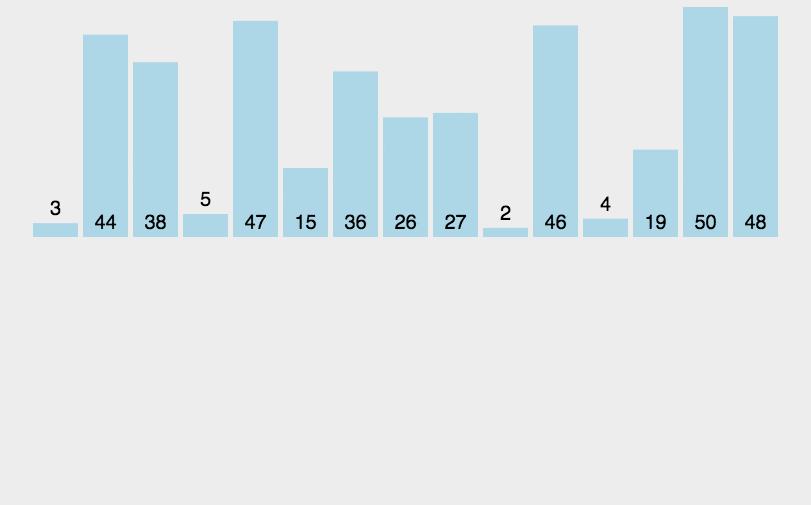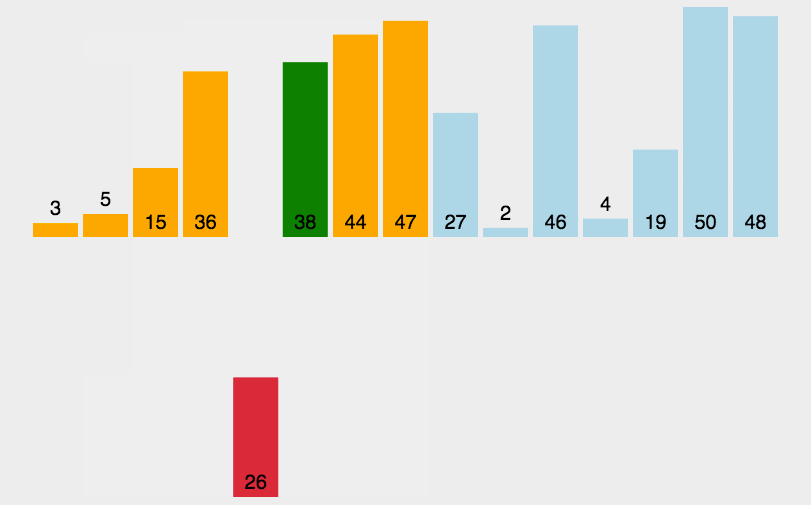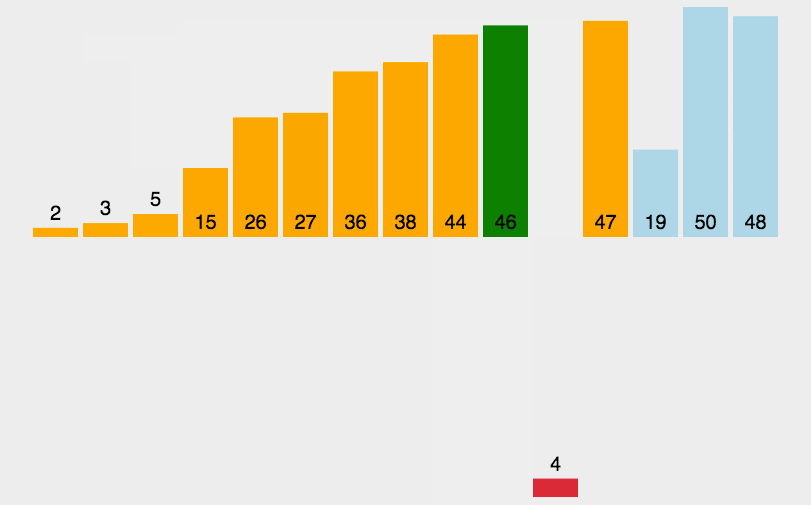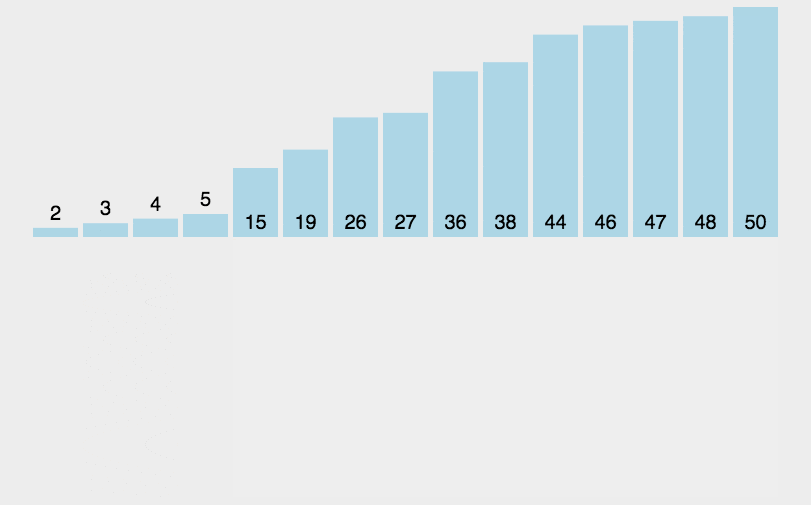
packagecom.itheima.mysort;publicclassA03_InsertDemo{publicstaticvoidmain(String[] args){/*
            插入排序：
                将0索引的元素到N索引的元素看做是有序的，把N+1索引的元素到最后一个当成是无序的。
                遍历无序的数据，将遍历到的元素插入有序序列中适当的位置，如遇到相同数据，插在后面。
                N的范围：0~最大索引

        */int[] arr ={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};//1.找到无序的哪一组数组是从哪个索引开始的。  2int startIndex =-1;for(int i =0; i < arr.length; i++){if(arr[i]> arr[i +1]){
                startIndex = i +1;break;}}//2.遍历从startIndex开始到最后一个元素，依次得到无序的哪一组数据中的每一个元素for(int i = startIndex; i < arr.length; i++){//问题：如何把遍历到的数据，插入到前面有序的这一组当中//记录当前要插入数据的索引int j = i;while(j >0&& arr[j]< arr[j -1]){//交换位置int temp = arr[j];
                arr[j]= arr[j -1];
                arr[j -1]= temp;
                j--;}}printArr(arr);}privatestaticvoidprintArr(int[] arr){//3.遍历数组for(int i =0; i < arr.length; i++){System.out.print(arr[i]+" ");}System.out.println();}}

4. 快速排序

快速排序是由东尼·霍尔所发展的一种排序算法。

快速排序又是一种分而治之思想在排序算法上的典型应用。

快速排序的名字起的是简单粗暴，因为一听到这个名字你就知道它存在的意义，就是快，而且效率高！

它是处理大数据最快的排序算法之一了。

4.1 算法步骤

1. 从数列中挑出一个元素，一般都是左边第一个数字，称为 “基准数”;
2. 创建两个指针，一个从前往后走，一个从后往前走。
3. 先执行后面的指针，找出第一个比基准数小的数字
4. 再执行前面的指针，找出第一个比基准数大的数字
5. 交换两个指针指向的数字
6. 直到两个指针相遇
7. 将基准数跟指针指向位置的数字交换位置，称之为：基准数归位。
8. 第一轮结束之后，基准数左边的数字都是比基准数小的，基准数右边的数字都是比基准数大的。
9. 把基准数左边看做一个序列，把基准数右边看做一个序列，按照刚刚的规则递归排序

4.2 动图演示

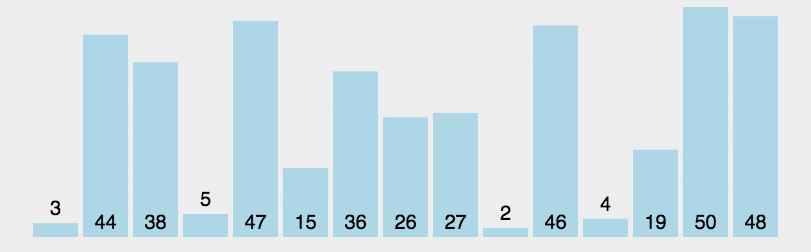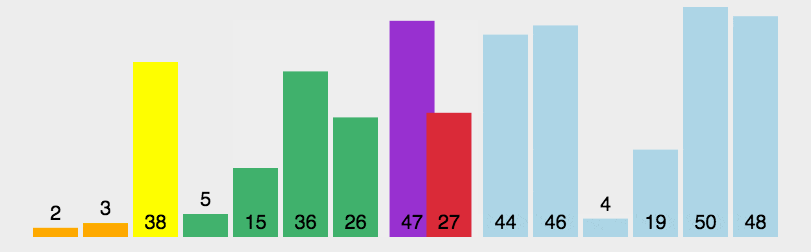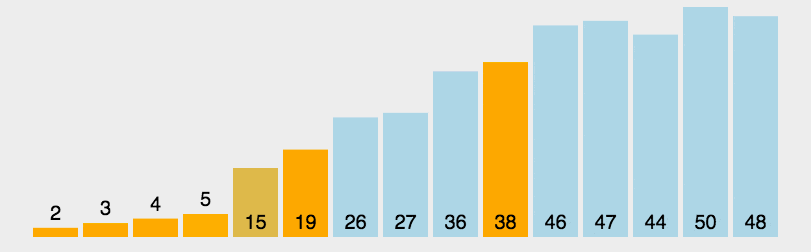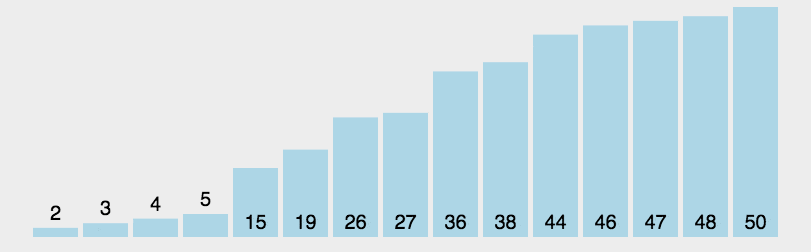
packagecom.itheima.mysort;importjava.util.Arrays;publicclassA05_QuickSortDemo{publicstaticvoidmain(String[] args){System.out.println(Integer.MAX_VALUE);System.out.println(Integer.MIN_VALUE);/*
       快速排序：
           第一轮：以0索引的数字为基准数，确定基准数在数组中正确的位置。
           比基准数小的全部在左边，比基准数大的全部在右边。
           后面以此类推。
     */int[] arr ={1,1,6,2,7,9,3,4,5,1,10,8};//int[] arr = new int[1000000];/* Random r = new Random();
       for (int i = 0; i < arr.length; i++) {
           arr[i] = r.nextInt();
       }*/long start =System.currentTimeMillis();quickSort(arr,0, arr.length -1);long end =System.currentTimeMillis();System.out.println(end - start);//149System.out.println(Arrays.toString(arr));//课堂练习：//我们可以利用相同的办法去测试一下，选择排序，冒泡排序以及插入排序运行的效率//得到一个结论：快速排序真的非常快。/* for (int i = 0; i < arr.length; i++) {
           System.out.print(arr[i] + " ");
       }*/}/*
    *   参数一：我们要排序的数组
    *   参数二：要排序数组的起始索引
    *   参数三：要排序数组的结束索引
    * */publicstaticvoidquickSort(int[] arr,int i,int j){//定义两个变量记录要查找的范围int start = i;int end = j;if(start > end){//递归的出口return;}//记录基准数int baseNumber = arr[i];//利用循环找到要交换的数字while(start != end){//利用end，从后往前开始找，找比基准数小的数字//int[] arr = {1, 6, 2, 7, 9, 3, 4, 5, 10, 8};while(true){if(end <= start || arr[end]< baseNumber){break;}
               end--;}System.out.println(end);//利用start，从前往后找，找比基准数大的数字while(true){if(end <= start || arr[start]> baseNumber){break;}
               start++;}//把end和start指向的元素进行交换int temp = arr[start];
           arr[start]= arr[end];
           arr[end]= temp;}//当start和end指向了同一个元素的时候，那么上面的循环就会结束//表示已经找到了基准数在数组中应存入的位置//基准数归位//就是拿着这个范围中的第一个数字，跟start指向的元素进行交换int temp = arr[i];
       arr[i]= arr[start];
       arr[start]= temp;//确定6左边的范围，重复刚刚所做的事情quickSort(arr,i,start -1);//确定6右边的范围，重复刚刚所做的事情quickSort(arr,start +1,j);}}

后记
👉👉💕💕美好的一天，到此结束，下次继续努力！欲知后续，请看下回分解，写作不易，感谢大家的支持！！ 🌹🌹🌹