C语言经典算法实例5：验证哥德巴赫猜想

C语言经典算法实例5：验证哥德巴赫猜想

一、问题描述

1.1、什么是哥德巴赫猜想

哥德巴赫1742年在给欧拉的信中提出了以下猜想：任一大于2的整数都可写成三个质数之和 。但是哥德巴赫自己无法证明它，于是就写信请教赫赫有名的大数学家欧拉帮忙证明，但是一直到死，欧拉也无法证明。 因现今数学界已经不使用“1也是素数”这个约定，原初猜想的现代陈述为：任一大于5的整数都可写成三个质数之和。(n>5：当n为偶数，n=2+(n-2)，n-2也是偶数，可以分解为两个质数的和；当n为奇数，n=3+(n-3)，n-3也是偶数，可以分解为两个质数的和)欧拉在回信中也提出另一等价版本，即任一大于2的偶数都可写成两个质数之和。今日常见的猜想陈述为欧拉的版本。把命题"任一充分大的偶数都可以表示成为一个素因子个数不超过a个的数与另一个素因子不超过b个的数之和"记作"a+b"。1966年陈景润证明了"1+2"成立，即"任一充分大的偶数都可以表示成二个素数的和，或是一个素数和一个半素数的和"。

1.2、什么是半素数

• 什么是半素数

两个素数的乘积所得的自然数
若一个自然数可以表示成两个素数乘积的形式，这个自然数就叫做半素数（又名半质数、二次殆素数）。

• 例如下面的一些数字为半素数。

4，6，9，10，14，15，21，22，25，26，33，34，35，38，39，46，49，51，55，57，58，62，65，69，74，77，82，85，86，87，91，93，94，95，106，111，115，118，119，121，122，123，129，133，134，141，142.

1.3、本文的问题描述

验证哥德巴赫猜想
问题的描述
如下几点所示

1. 任一充分大的偶数都可以表示成二个素数的和，或是一个素数和一个半素数的和。
2. 偶数输入的为大于6的偶数。
3. 对1-100之间的数字进行哥德巴赫猜想的验证。
4. 程序采用函数模块化的思路。

二、算法实例编译环境

本文C语言经典算法实例的编译环境，使用的是集成开发环境：Visual Studio 2019

Visual Studio 2019官网链接如下

Visual Studio 2019官网链接

Visual Studio 2019集成的开发环境的特点有

1. Visual Studio 2019默认安装Live Share代码协作服务。
2. 帮助用户快速编写代码的新欢迎窗口、改进搜索功能、总体性能改进。
3. Visual Studio IntelliCode AI帮助。
4. 更好的Python虚拟和Conda支持。
5. 以及对包括WinForms和WPF在内的.NET Core 3.0项目支持等

三、算法实例实现过程

3.1、包含头文件

包含头文件 代码如下所示

#pragmaonce// 包含头文件#include<stdio.h>#include<stdlib.h>#include<math.h>#include<stdbool.h>

• 将要用到的Ｃ语言头文件包含近年来。

3.2、声明变量

声明变量 代码如下所示

int a =0;

• 声明了变量a。
• 作为输入的变量使用。

3.３、输入一个大于 6 的偶数

输入一个大于 6 的偶数 代码如下所示

printf("输入一个大于 6 的偶数:");scanf("%d",&a);printf("\n");

• 声明相关变量min, max，row, col, n;

3.4、对输入的数字进行哥德巴赫猜想的验证

• 对输入的数字进行哥德巴赫猜想的验证采用函数的方式进行编写。

对输入的数字进行哥德巴赫猜想的验证 代码如下所示

1. 进行哥德巴赫猜想的验证函数的声明。

/// <summary>/// 对输入的数字进行哥德巴赫猜想的验证/// </summary>/// <param name="intNum">输入的数字</param>/// <returns>blFlag</returns>static bool ISGDBHArith(int intNum);

1. 进行哥德巴赫猜想的验证函数的定义。

/// <summary>/// 对输入的数字进行哥德巴赫猜想的验证/// </summary>/// <param name="intNum">输入的数字</param>/// <returns>blFlag</returns>static bool ISGDBHArith(int intNum){
    bool blFlag = false;// 标识是否符合哥德巴赫猜想 if(intNum %2==0&& intNum >6)// 对要判断的数字进行判断 {for(int i =1; i <= intNum /2; i++){
            bool bl1 =IsPrimeNumber(i);// 判断i 是否为素数 
            bool bl2 =IsPrimeNumber(intNum - i);// 判断 intNum-i 是否为素数 if(bl1 & bl2){//输出等式 printf("%d = %d + %d\n", intNum, i, intNum - i);
                blFlag = true;// 符合哥德巴赫猜想 }}}return blFlag;// 返回bool 型变量 }

• 对输入的数字进行哥德巴赫猜想的验证。
• 函数返回为bool类型的变量：blFlag。

3.5、判断输入的数字是否为素数。

• 判断输入的数字是否为素数，采用函数的方式编写。

判断输入的数字是否为素数，代码如下所示

1. 判断输入的数字是否为素数的函数声明。

/// <summary>/// 判断输入的数字是否为素数。/// </summary>/// <param name="intNum">输入的数字</param>/// <returns>blFlag</returns>static bool IsPrimeNumber(int intNum);

1. 判断输入的数字是否为素数的函数定义。

/// <summary>/// 判断输入的数字是否为素数。/// </summary>/// <param name="intNum">输入的数字</param>/// <returns>blFlag</returns>static bool IsPrimeNumber(int intNum){
    bool blFlag = true;// 标识是否是素数 if(intNum ==1|| intNum ==2)// 判断输入的数字是否是 1 或者 2 {
        blFlag = true;// 为bool 类型变量赋值 }else{int sqr =(int)(sqrt((double)intNum));// 对要判断的数字进行开方运算 for(int i = sqr; i >=2; i--)// 从开方后的数进行循环 {if(intNum % i ==0)// 对要判断的数字和指定数字进行求余运算 {
                blFlag = false;// 如果余数为 0，说明不是素数 }}}return blFlag;// 返回bool 型变量 }

• 判断输入的数字是否为素数。
• 函数返回为bool类型的变量：blFlag。

按F5进行编译，调试结果如下所示。

• 可以正确的输出我们向数组中输入的数据。

3.6、对输入的数字进行哥德巴赫猜想的判断

对输入的数字进行哥德巴赫猜想的判断 代码如下所示

if(blFlag){printf("\n%d：能写成两个素数的和,所以其符合哥德巴赫猜想。\n\n", a);}else{printf("\n%d：不能写成两个素数的和,所以其不符合哥德巴赫猜想。\n\n", a);}

• 如果输入的数字能写成两个素数的和，则符合哥德巴赫猜想。
• 如果输入的数字不能写成两个素数的和，则不符合哥德巴赫猜想。

按F5进行编译，调试结果如下所示。

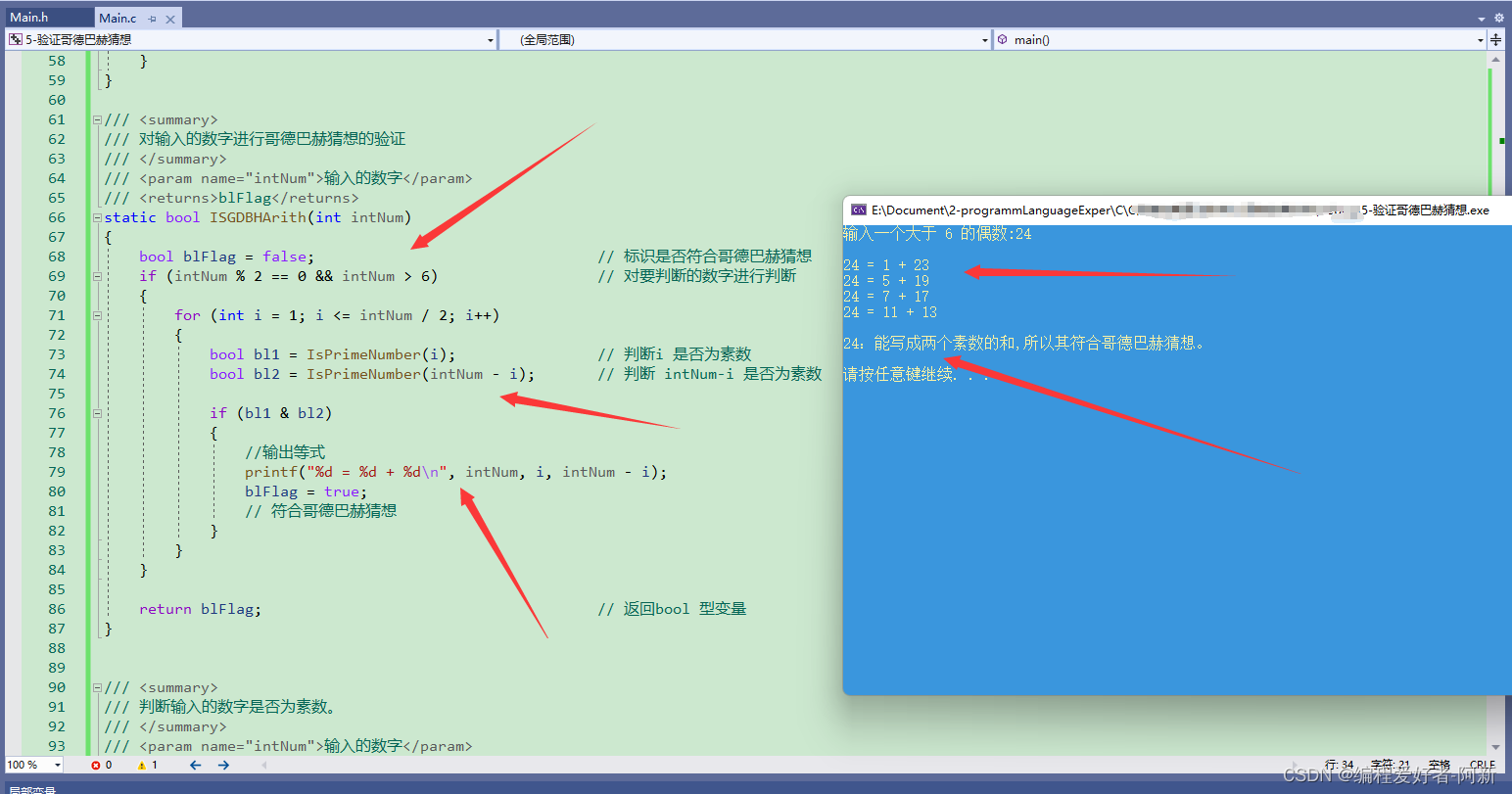
3.7、判断数字1-100是否符合哥德巴赫猜想。

• 判断数字1-100是否符合哥德巴赫猜想采用函数编写的方式。

判断数字1-100是否符合哥德巴赫猜想 代码如下所示。

1. 判断数字1-100是否符合哥德巴赫猜想的函数声明。

/// <summary>/// 判断数字1-100是否符合哥德巴赫猜想。/// </summary>voiddigitJudge();

1. 判断数字1-100是否符合哥德巴赫猜想的函数定义。

/// <summary>/// 判断数字1-100是否符合哥德巴赫猜想。/// </summary>voiddigitJudge(){for(int i =1; i <=100; i++){
        bool blFlag =ISGDBHArith(i);// 判断是否符合哥德巴赫猜想 if(blFlag){printf("\n%d：能写成两个素数的和,所以其符合哥德巴赫猜想。\n\n", i);}else{printf("\n%d：不能写成两个素数的和,所以其不符合哥德巴赫猜想。\n\n", i);}printf("\n");}}

• 使用for循环的方式。
• 判断数字1-100是否符合哥德巴赫猜想。

按F5进行编译，调试结果如下所示。

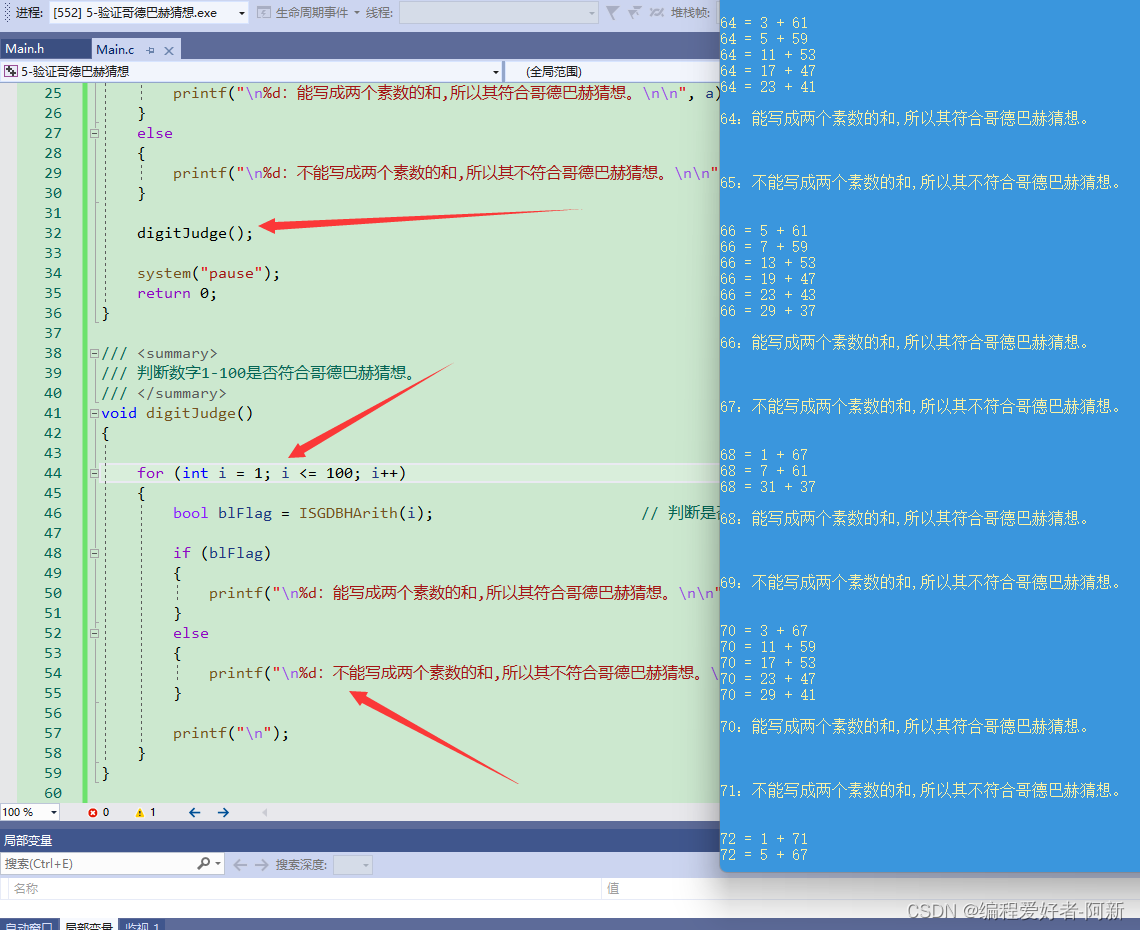
输入一个大于 6 的偶数:2424=1+2324=5+1924=7+1724=11+1324：能写成两个素数的和,所以其符合哥德巴赫猜想。

1：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

2：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

3：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

4：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

5：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

6：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

7：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

8=1+78=3+58：能写成两个素数的和,所以其符合哥德巴赫猜想。

9：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

10=3+710=5+510：能写成两个素数的和,所以其符合哥德巴赫猜想。

11：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

12=1+1112=5+712：能写成两个素数的和,所以其符合哥德巴赫猜想。

13：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

14=1+1314=3+1114=7+714：能写成两个素数的和,所以其符合哥德巴赫猜想。

15：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

16=3+1316=5+1116：能写成两个素数的和,所以其符合哥德巴赫猜想。

17：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

18=1+1718=5+1318=7+1118：能写成两个素数的和,所以其符合哥德巴赫猜想。

19：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

20=1+1920=3+1720=7+1320：能写成两个素数的和,所以其符合哥德巴赫猜想。

21：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

22=3+1922=5+1722=11+1122：能写成两个素数的和,所以其符合哥德巴赫猜想。

23：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

24=1+2324=5+1924=7+1724=11+1324：能写成两个素数的和,所以其符合哥德巴赫猜想。

25：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

26=3+2326=7+1926=13+1326：能写成两个素数的和,所以其符合哥德巴赫猜想。

27：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

28=5+2328=11+1728：能写成两个素数的和,所以其符合哥德巴赫猜想。

29：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

30=1+2930=7+2330=11+1930=13+1730：能写成两个素数的和,所以其符合哥德巴赫猜想。

31：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

32=1+3132=3+2932=13+1932：能写成两个素数的和,所以其符合哥德巴赫猜想。

33：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

34=3+3134=5+2934=11+2334=17+1734：能写成两个素数的和,所以其符合哥德巴赫猜想。

35：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

36=5+3136=7+2936=13+2336=17+1936：能写成两个素数的和,所以其符合哥德巴赫猜想。

37：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

38=1+3738=7+3138=19+1938：能写成两个素数的和,所以其符合哥德巴赫猜想。

39：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

40=3+3740=11+2940=17+2340：能写成两个素数的和,所以其符合哥德巴赫猜想。

41：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

42=1+4142=5+3742=11+3142=13+2942=19+2342：能写成两个素数的和,所以其符合哥德巴赫猜想。

43：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

44=1+4344=3+4144=7+3744=13+3144：能写成两个素数的和,所以其符合哥德巴赫猜想。

45：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

46=3+4346=5+4146=17+2946=23+2346：能写成两个素数的和,所以其符合哥德巴赫猜想。

47：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

48=1+4748=5+4348=7+4148=11+3748=17+3148=19+2948：能写成两个素数的和,所以其符合哥德巴赫猜想。

49：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

50=3+4750=7+4350=13+3750=19+3150：能写成两个素数的和,所以其符合哥德巴赫猜想。

51：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

52=5+4752=11+4152=23+2952：能写成两个素数的和,所以其符合哥德巴赫猜想。

53：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

54=1+5354=7+4754=11+4354=13+4154=17+3754=23+3154：能写成两个素数的和,所以其符合哥德巴赫猜想。

55：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

56=3+5356=13+4356=19+3756：能写成两个素数的和,所以其符合哥德巴赫猜想。

57：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

58=5+5358=11+4758=17+4158=29+2958：能写成两个素数的和,所以其符合哥德巴赫猜想。

59：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

60=1+5960=7+5360=13+4760=17+4360=19+4160=23+3760=29+3160：能写成两个素数的和,所以其符合哥德巴赫猜想。

61：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

62=1+6162=3+5962=19+4362=31+3162：能写成两个素数的和,所以其符合哥德巴赫猜想。

63：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

64=3+6164=5+5964=11+5364=17+4764=23+4164：能写成两个素数的和,所以其符合哥德巴赫猜想。

65：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

66=5+6166=7+5966=13+5366=19+4766=23+4366=29+3766：能写成两个素数的和,所以其符合哥德巴赫猜想。

67：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

68=1+6768=7+6168=31+3768：能写成两个素数的和,所以其符合哥德巴赫猜想。

69：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

70=3+6770=11+5970=17+5370=23+4770=29+4170：能写成两个素数的和,所以其符合哥德巴赫猜想。

71：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

72=1+7172=5+6772=11+6172=13+5972=19+5372=29+4372=31+4172：能写成两个素数的和,所以其符合哥德巴赫猜想。

73：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

74=1+7374=3+7174=7+6774=13+6174=31+4374=37+3774：能写成两个素数的和,所以其符合哥德巴赫猜想。

75：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

76=3+7376=5+7176=17+5976=23+5376=29+4776：能写成两个素数的和,所以其符合哥德巴赫猜想。

77：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

78=5+7378=7+7178=11+6778=17+6178=19+5978=31+4778=37+4178：能写成两个素数的和,所以其符合哥德巴赫猜想。

79：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

80=1+7980=7+7380=13+6780=19+6180=37+4380：能写成两个素数的和,所以其符合哥德巴赫猜想。

81：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

82=3+7982=11+7182=23+5982=29+5382=41+4182：能写成两个素数的和,所以其符合哥德巴赫猜想。

83：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

84=1+8384=5+7984=11+7384=13+7184=17+6784=23+6184=31+5384=37+4784=41+4384：能写成两个素数的和,所以其符合哥德巴赫猜想。

85：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

86=3+8386=7+7986=13+7386=19+6786=43+4386：能写成两个素数的和,所以其符合哥德巴赫猜想。

87：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

88=5+8388=17+7188=29+5988=41+4788：能写成两个素数的和,所以其符合哥德巴赫猜想。

89：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

90=1+8990=7+8390=11+7990=17+7390=19+7190=23+6790=29+6190=31+5990=37+5390=43+4790：能写成两个素数的和,所以其符合哥德巴赫猜想。

91：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

92=3+8992=13+7992=19+7392=31+6192：能写成两个素数的和,所以其符合哥德巴赫猜想。

93：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

94=5+8994=11+8394=23+7194=41+5394=47+4794：能写成两个素数的和,所以其符合哥德巴赫猜想。

95：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

96=7+8996=13+8396=17+7996=23+7396=29+6796=37+5996=43+5396：能写成两个素数的和,所以其符合哥德巴赫猜想。

97：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

98=1+9798=19+7998=31+6798=37+6198：能写成两个素数的和,所以其符合哥德巴赫猜想。

99：不能写成两个素数的和,所以其不符合哥德巴赫猜想。

100=3+97100=11+89100=17+83100=29+71100=41+59100=47+53100：能写成两个素数的和,所以其符合哥德巴赫猜想。

请按任意键继续...

四、经典算法实例程序 完整代码

经典算法实例程序完整代码如下所示

4.1、main.h文件

#pragmaonce// 包含头文件#include<stdio.h>#include<stdlib.h>#include<math.h>#include<stdbool.h>/// <summary>/// 判断数字1-100是否符合哥德巴赫猜想。/// </summary>voiddigitJudge();/// <summary>/// 对输入的数字进行哥德巴赫猜想的验证/// </summary>/// <param name="intNum">输入的数字</param>/// <returns>blFlag</returns>static bool ISGDBHArith(int intNum);/// <summary>/// 判断输入的数字是否为素数。/// </summary>/// <param name="intNum">输入的数字</param>/// <returns>blFlag</returns>static bool IsPrimeNumber(int intNum);

4.2、main.c文件

#define_CRT_SECURE_NO_WARNINGS#include"Main.h"/// <summary>/// 主函数/// </summary>/// <returns>返回0</returns>intmain(){system("color 3E");int a =0;printf("输入一个大于 6 的偶数:");scanf("%d",&a);printf("\n");

    bool blFlag =ISGDBHArith(a);// 判断是否符合哥德巴赫猜想 if(blFlag){printf("\n%d：能写成两个素数的和,所以其符合哥德巴赫猜想。\n\n", a);}else{printf("\n%d：不能写成两个素数的和,所以其不符合哥德巴赫猜想。\n\n", a);}digitJudge();system("pause");return0;}/// <summary>/// 判断数字1-100是否符合哥德巴赫猜想。/// </summary>voiddigitJudge(){for(int i =1; i <=100; i++){
        bool blFlag =ISGDBHArith(i);// 判断是否符合哥德巴赫猜想 if(blFlag){printf("\n%d：能写成两个素数的和,所以其符合哥德巴赫猜想。\n\n", i);}else{printf("\n%d：不能写成两个素数的和,所以其不符合哥德巴赫猜想。\n\n", i);}printf("\n");}}/// <summary>/// 对输入的数字进行哥德巴赫猜想的验证/// </summary>/// <param name="intNum">输入的数字</param>/// <returns>blFlag</returns>static bool ISGDBHArith(int intNum){
    bool blFlag = false;// 标识是否符合哥德巴赫猜想 if(intNum %2==0&& intNum >6)// 对要判断的数字进行判断 {for(int i =1; i <= intNum /2; i++){
            bool bl1 =IsPrimeNumber(i);// 判断i 是否为素数 
            bool bl2 =IsPrimeNumber(intNum - i);// 判断 intNum-i 是否为素数 if(bl1 & bl2){//输出等式 printf("%d = %d + %d\n", intNum, i, intNum - i);
                blFlag = true;// 符合哥德巴赫猜想 }}}return blFlag;// 返回bool 型变量 }/// <summary>/// 判断输入的数字是否为素数。/// </summary>/// <param name="intNum">输入的数字</param>/// <returns>blFlag</returns>static bool IsPrimeNumber(int intNum){
    bool blFlag = true;// 标识是否是素数 if(intNum ==1|| intNum ==2)// 判断输入的数字是否是 1 或者 2 {
        blFlag = true;// 为bool 类型变量赋值 }else{int sqr =(int)(sqrt((double)intNum));// 对要判断的数字进行开方运算 for(int i = sqr; i >=2; i--)// 从开方后的数进行循环 {if(intNum % i ==0)// 对要判断的数字和指定数字进行求余运算 {
                blFlag = false;// 如果余数为 0，说明不是素数 }}}return blFlag;// 返回bool 型变量 }

五、总结

本文的C语言经典算法实例：求二维数组最大最小值，要实现的目标如下

1. 任一充分大的偶数都可以表示成二个素数的和，或是一个素数和一个半素数的和。
2. 偶数输入的为大于6的偶数。
3. 对1-100之间的数字进行哥德巴赫猜想的验证。
4. 程序采用函数模块化的思路。

文到这里就结束啦。
希望本文的C语言经典算法实例：验证哥德巴赫猜想。
能激发你对C语言以及算法学习的热爱。

• 你的支持是对我最大的鼓励。