2023五一数学建模A题完整思路

已更新五一数学建模A题思路，文章末尾获取！

A题完整思路：

A题是一个动力学问题，需要我们将物理学概念运用到实际生活中，我们可以先看题目

问题1：****假设无人机以平行于水平面的方式飞行，在空中投放物资（物资为球形，半径20cm，重量50kg）到达地面指定位置。

（1）建立数学模型，给出无人机投放距离（投放物资时无人机与地面物资指定落地点之间的直线距离）与无人机飞行高度、飞行速度、空气阻力等之间的关系。

我们可以使用自由落体运动和抛物线运动的原理来建立数学模型。在此模型中，我们需要考虑无人机的飞行高度（h）、飞行速度（v0）、空气阻力（k）以及投放距离（d）之间的关系。假设物资的质量为m，重力加速度为g，投放时刻物资的水平速度为vx0，竖直速度为vy0。

首先，我们来考虑竖直方向上的运动。物资受到重力和空气阻力的作用，运动方程可以表示为：

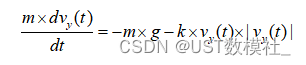
我们需要求解这个微分方程，得到物资在竖直方向上的速度随时间的变化关系vy（t）

然后我们可以通过求解物资的竖直运动方程来得到物资的落地时间：

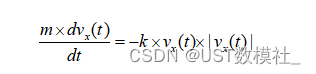
当物资落地时，h(t) = 0，我们可以求解出落地时间t。

接下来，考虑物资在水平方向上的运动。物资受到空气阻力的作用，运动方程可以表示为：

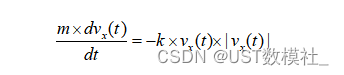
我们需要求解这个微分方程，得到物资在水平方向上的速度随时间的变化关系vx（t）。然后我们可以通过求解物资的水平运动方程来得到物资在水平方向上的位移：

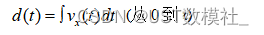
最后，我们将t代入d(t)中，得到投放距离d。

（2）假设无人机的飞行高度为300m，飞行速度为300km/h，风速为5m/s，风向与水平面平行。建立数学模型，分别给出无人机飞行方向与风向相同（夹角为0度）、相反（夹角为180度）、垂直（夹角为90度）情况下无人机的投放距离。

根据题目给定的条件，我们可以将具体数值代入模型中，分别计算出不同风向条件下的投放距离。由于风速和风向会影响空气阻力和物资的水平速度，我们需要根据风向调整模型中的参数。以下是三种情况的计算方法：

当夹角为0度（风向与无人机飞行方向相同）： 在这种情况下，风速会使物资的水平速度增加。因此，在水平方向上的初始速度为：

vx0=v0+风速

夹角为180度（风向与无人机飞行方向相反）： 在这种情况下，风速会使物资的水平速度减小。因此，在水平方向上的初始速度为：

vx0=v0-风速

夹角为90度（风向与无人机飞行方向垂直）： 在这种情况下，风速不会改变物资的水平速度，但会对物资产生横向位移。我们可以在模型中加入横向速度的影响。因此，在水平方向上的初始速度为：

vx0=v0

问题2：无人机不仅能定点投放物资，而且还可以通过安装在无人机前端的发射筒发射爆炸物疏通河道。其大致过程是：无人机首先水平飞行接近障碍物所处区域，然后俯冲找准时机发射爆炸物，发射结束后无人机随即拉升飞走。现有一处河流被冰块堆积阻断，需要用无人机发射爆炸物（爆炸物为球形，半径8cm，重量5kg）对目标进行爆破。假设无人机的初始点到目标的水平距离为10000m。受环境影响，无人机必须俯冲发射，并且发射方向与无人机的飞行方向一致。

建立数学模型，给出无人机发射距离（发射点与目标的直线距离）与无人机的飞行高度、飞行速度、俯冲角度及发射速度等因素之间的关系。

解答：我们可以采用类似问题1中的方法，利用物理学原理建立数学模型。在此模型中，我们需要考虑无人机的飞行高度（h）、飞行速度（v0）、俯冲角度（θ）、发射速度（v1）以及发射距离（d）之间的关系。假设发射时刻爆炸物的水平速度为vx0，竖直速度为vy0。

首先，我们需要将无人机的飞行速度和发射速度转换为水平和竖直方向上的速度分量。设无人机俯冲角度为θ，则：

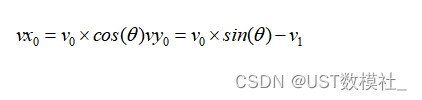
接下来，我们可以分别考虑爆炸物在水平和竖直方向上的运动。与问题1类似，我们需要求解爆炸物在竖直方向上的运动方程，得到落地时间t。然后，我们可以通过求解爆炸物在水平方向上的运动方程来得到爆炸物在水平方向上的位移，即发射距离d。

最后，我们将t代入d中，得到发射距离d与无人机的飞行高度、飞行速度、俯冲角度及发射速度等因素之间的关系。

（2）假设风速为6m/s，无人机接近目标时的飞行高度为800m、飞行速度为300km/h，爆炸物的发射速度为600km/h（相对于无人机的速度）。要求发射爆炸物时无人机与目标的距离在1000 m-3000 m之间，且无人机的高度不低于300m，请给出无人机击中目标的发射策略。

根据题目给定的条件，我们把具体数值代入模型中。先选择一个合适的俯冲角度θ，使得无人机在发射爆炸物时满足高度不低于300m的要求。在这个过程中，我们可以通过迭代法或其他优化方法来寻找最优的θ。

确定了合适的俯冲角度θ后，把它其代入模型中，计算出发射距离d。接下来，我们需要确定无人机与目标的距离在1000m-3000m之间。我们可以根据给定的飞行高度、飞行速度、发射速度和风速，通过模型计算出满足条件的无人机与目标的距离范围。在找到满足条件的距离范围后，我们可以根据实际情况选择一个最佳的发射策略。例如，选择距离较近的发射点以提高命中概率，或者选择距离较远的发射点以确保无人机的安全。

问题3：无人机发射爆炸物命中目标的精度与无人机飞行的稳定性有很大关系。相同条件下，无人机发射爆炸物时越稳定，命中目标的精度越高。开始俯冲后，无人机操控员需要不断调整无人机的飞行姿态以修正风向、风速对无人机的影响。

1. 在飞行速度、发射速度一定的情况下，综合考虑各种因素，建立数学模型，量化无人机飞行的稳定性，给出稳定性与命中精度之间的关系，并利用数值仿真等方法对无人机的稳定性进行分析验证。

要去量化无人机飞行的稳定性，我们引入一个稳定性参数S。S可以通过以下几个因素来描述：无人机的飞行速度（v0）、俯冲角度（θ）、风速（w）以及风向与无人机飞行方向的夹角（α）。稳定性参数S的计算方法可以使用基于物理原理的动力学模型，或者使用机器学习等数据驱动的方法根据历史数据进行拟合。

稳定性参数S与命中精度之间的关系可以通过建立概率模型来描述。例如，我们可以假设命中精度P与稳定性参数S之间存在如下关系：

P = f(S)

其中，f为关系函数。我们可以通过分析实验数据或者利用数值仿真等方法来确定f的具体形式。

更多思路↓↓