不使用直方图的6个原因以及应该使用哪个图替代

直方图并非没有偏见。实际上，它们是武断的，可能会导致对数据的错误结论。

无论你是在与高管开会，还是在与数据狂人开会，有一件事是可以肯定的:总会看到一个直方图。

直方图非常直观:任何人一眼就能理解它们。此外，它们是对现实的不偏不倚的反映，对吧?其实不是这样。

直方图可能会误导人，并得出错误的结论——即使是简单的数据!

在这篇文章中，我们将通过一些例子来解释为什么直方图不是可视化数据的最佳选择:

1. 它的显示太依赖装箱的数量。
2. 它太依赖于变量的最大值和最小值。
3. 它不能检测相关值。
4. 它不能区分连续和离散变量。
5. 无法观察和比较数据的分布
6. 不加载所有数据，就很难做出判断。

在本文的最后，我将推荐另一种解决方案，称为CDP，它可以克服这些缺陷。

直方图怎么了？

1、显示太依赖装箱的数量。

要绘制直方图，必须首先确定间隔数（也称为箱）。有很多不同的经验法则可以做到这一点（有关概述，请参阅此页面）。但是这个选择有多关键？让我们获取一些真实数据，看看直方图如何根据分箱数变化。

变量是303人在某些体育活动中达到的最大心率（每分钟心跳数）（数据来自UCI心脏病数据集）。

查看左上图（在Python和R中默认情况下得到），我们会看到一个具有单个峰（模式）的良好分布的印象。但是，如果我们查看其他直方图，则会得到完全不同的图片。直方图可以得出矛盾的结论。

2、它太依赖于变量的最大值和最小值。

即使设置了箱数，间隔也取决于变量的最小和最大位置。只需稍微改变其中之一，并且所有间隔都改变即可。换句话说，直方图不是鲁棒的。

例如，让我们尝试更改变量的最大值，同时将箱数保持不变。

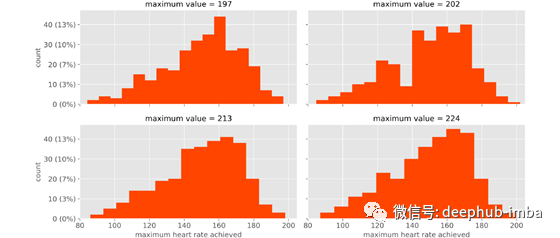
如果单个值不同，则整个图将不同。这是不受欢迎的属性，因为我们对整体分布感兴趣：单个值应该没有区别！

3、不能检测相关值。

通常，当变量包含一些频繁的值时，我们需要意识到这一点。但是，直方图不允许这样做，因为直方图是基于间隔的，并且间隔“隐藏”了各个值。

一个经典的例子是，缺失值被大量推算为0。例如，让我们看一个由1万个数据点组成的变量，其中26％为0。

左边的图是使用默认参数得到的。通过观察它，你会相信这个变量有一个“平滑”的行为，你甚至不会察觉到有非常多0。

右边的图是通过缩小箱子得到的，并给出了一个更清晰的现实表现。但问题是，无论你如何缩小容器的范围，你永远无法确定第一个容器中是否只包含0或其他一些值。

4、不能区分连续和离散变量。

一般来说，我们想知道一个数值变量是连续的还是离散的。根据直方图，这几乎是不可能的。

让我们以变量“年龄”为例。你会发现Age = 49岁(当年龄被截短)，或者Age = 49.828884325804246岁(当年龄用出生后的天数除以365.25计算)。第一个是离散变量，而第二个是连续变量。

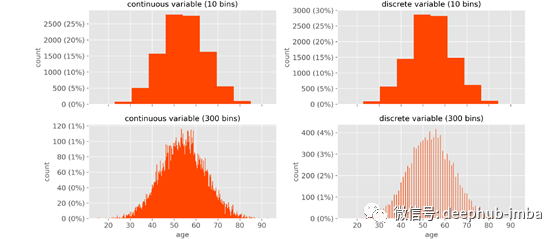
左边的是连续的，右边的是离散的。然而，在上面的图(默认值)中，你不会看到两者之间有任何区别:它们看起来完全一样。

5、无法观察和比较数据的分布

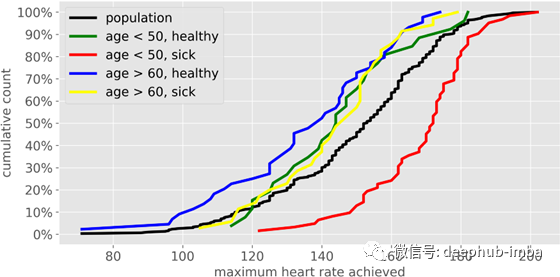
通常有必要在不同的集群上比较相同的变量。例如，关于上面的UCI心脏病数据，我们可能想要比较:

1. 全体人口(作为参考)
2. 50岁以下心脏病患者
3. 50岁以下且没有心脏病的人
4. 60岁以上心脏病患者
5. 60岁以上且没有心脏病的人

我们会得到这样的结果:

直方图是基于区域的，当我们试图进行比较时，区域最终会重叠，这使得我们的工作不可能完成。

6、不加载所有数据，就很难做出判断。

如果你在Excel、R或Python中拥有所有数据，那么制作直方图很容易:在Excel中，你只需单击直方图图标，在R中执行命令hist(x)，而在Python中则是plt.hist(x)。

但是假设你的数据存储在数据库中。你不想下载所有的数据只是为了制作一个直方图，对吧?基本上，你所需要的只是一个包含每个容器的极端间隔和观测计数的表。是这样的:

 | INTERVAL_LEFT | INTERVAL_RIGHT | COUNT         |
 |---------------|----------------|---------------|
 | 75.0          | 87.0           | 31            |
 | 87.0          | 99.0           | 52            |
 | 99.0          | 111.0          | 76            |
 | ...           | ...            | ...           |

但是通过SQL查询获取它并不像看起来那么简单。例如，Big Query代码是:

 WITH
 STATS AS (
   SELECT 
     COUNT(*) AS N,
     APPROX_QUANTILES(VARIABLE_NAME, 4) AS QUARTILES
   FROM
     TABLE_NAME
 ),
 BIN_WIDTH AS (
   SELECT
     -- freedman-diaconis formula for calculating the bin width
     (QUARTILES[OFFSET(4)] — QUARTILES[OFFSET(0)]) / ROUND((QUARTILES[OFFSET(4)] — QUARTILES[OFFSET(0)]) / (2 * (QUARTILES[OFFSET(3)] — QUARTILES[OFFSET(1)]) / POW(N, 1/3)) + .5) AS FD
   FROM 
     STATS
 ),
 HIST AS (
   SELECT 
     FLOOR((TABLE_NAME.VARIABLE_NAME — STATS.QUARTILES[OFFSET(0)]) / BIN_WIDTH.FD) AS INTERVAL_ID,
     COUNT(*) AS COUNT
   FROM 
     TABLE_NAME,
     STATS,
     BIN_WIDTH
   GROUP BY 
     1
 )
 SELECT 
   STATS.QUARTILES[OFFSET(0)] + BIN_WIDTH.FD * HIST.INTERVAL_ID AS INTERVAL_LEFT,
   STATS.QUARTILES[OFFSET(0)] + BIN_WIDTH.FD * (HIST.INTERVAL_ID + 1) AS INTERVAL_RIGHT,
   HIST.COUNT
 FROM 
   HIST, 
   STATS, 
   BIN_WIDTH

这显然不是有点麻烦能够形容的

另一种选择:累积分布图（Cumulative Distribution）

在看到为什么直方图不是理想选择的6个原因后，一个自然的问题是:“我还有其他选择吗?”这里确实存在一个更好的替代方案，称为“累积分布图”(CDP)。我知道这个名字不太容易记住，但我保证值得。

累积分布图是一个变量的分位数分布图。换句话说，CDP上的每个点显示:

x轴:变量的原始值(正如直方图所示);

y轴:有多少个是与观察值相同或少于观察值的数量。

让我们来看一个常见变量的例子:最大心率。

我们取坐标为x = 140 y = 90(30%)的点。在横轴上，你可以看到变量的值:每分钟140次心跳。在纵轴上，你可以看到心率等于或低于140的观察计数(在本例中是90人，这意味着样本的30%)。因此，30%的样本每分钟心跳次数不超过140次。

告诉你有多少观察值“等于或低于”某一给定水平有什么意义呢?为什么不只是“平等”? 因为如果不这样做，结果将取决于变量的单个值。这是行不通的，因为每个值只有很少的观察值（如果变量是连续的，通常只有一个）。相反，CDP依赖于分位数，这些分位数更加稳定，有意义并且易于阅读。

此外，如果你经常需要回答这样的问题:“有多少人在140和160之间?”或“180以上的有多少?”CDP将更有用。如果你仔细想想，CDP可以立即给一个答案。使用直方图是不可能的。

CDP解决了我们上面已经看到的所有问题。实际上，与直方图相比：

1.它不需要用户选择。给定一些数据，只有一个可能的CDP。

2.它没有异常值。由于分位数不变，因此极值对CDP没有影响。

3.它允许检测相关值。如果数据点集中在某个特定值上，则可以立即看到，因为会有一个垂直的部分划分为该值的对应关系。

4.乍一看，它可以识别离散变量。如果只有一堆可能的值（即变量是离散的），则可以立即看出来，因为曲线是阶梯形的。

5.可以轻松比较分布。比较同一图上的两个或多个分布很容易，因为它们只是曲线，而不是面积。而且，y轴始终在0到100％之间，从而使比较更加直接。例如，这是我们上面看到的示例：

没有所有的数据都可以轻松置作。因为需要的只是分位数，可以在SQL中轻松获得：

 SELECT 
   COUNT(*) AS N,
   APPROX_QUANTILES(VARIABLE_NAME, 100) AS PERCENTILES
 FROM
   TABLE_NAME

如何在Excel, R, Python中制作一个累积分布图

在Excel中，需要构建两列。第一个有101个数字，从0到1平均分布。第二列应该包含百分位数，可以通过公式:==PERCENTILE(DATA, *FRAC)*得到，其中DATA是包含数据的向量，FRAC是第一列:0.00,0.01,0.02,0.03，…，0.98,0.99,1。然后，你只需要画出这两列，注意把变量的值放在x轴上。

使用R的话就更加简单

 plot(ecdf(data))

在Python中则要引用一些辅助的包:

 from statsmodels.distributions.empirical_distribution import ECDF
 import matplotlib.pyplot as plt
 
 ecdf = ECDF(data)
 plt.plot(ecdf.x, ecdf.y)

感谢你的阅读!我希望这篇文章对你有用。

作者：Samuele Mazzanti

原文地址：https://towardsdatascience.com/6-reasons-why-you-should-stop-using-histograms-and-which-plot-you-should-use-instead-31f937a0a81c

deephub翻译组