本科课程【数据结构与算法】实验5 - 广度优先搜索、二叉排序树的构造

文章目录

大家好，我是【1+1=王】， 热爱java的计算机（人工智能）渣硕研究生在读。
如果你也对java、人工智能等技术感兴趣，欢迎关注，抱团交流进大厂！！！
Good better best, never let it rest, until good is better, and better best.

近期会把自己本科阶段的一些课程设计、实验报告等分享出来，供大家参考，希望对大家有帮助。

博客更新至专栏【课程设计实验报告】：https://blog.csdn.net/weixin_43598687/category_11640051.html

一、 实验目的

1. 掌握图的邻接表存储结构
2. 实现图的广度优先搜索
3. 掌握二叉排序树的链式存储结构
4. 实现二叉排序树的构造

二、 实验内容

1. 实验任务

（1）建立一个无向连通图，用广度优先搜索（BFS）遍历
（2）输入一串数字，建立二叉排序树

2. 程序设计

1） 数据输入（输入哪些数据、个数、类型、来源、输入方式）
无向图的顶点数据（data）char字符型；
无向图的边关系（v1,v2）int 整型；
各边的权值（w）int 整型

二叉树的结点关键数（key）int整型

2） 数据存储（输入数据在内存中的存储）
采用new方法动态分配空间，以邻接表存储

采用new 动态分配空间，储存在*BinSearchTree中
3） 数据处理（说明处理步骤。若不是非常简单，需要绘制流程图）

①建立邻接表储存无向图
输入总顶点数和总边数；
建立顶点表（依次输入点的信息存入顶点表中，使每个表头节点的指针域初始化NULL）
创建邻接表（依次输入每条边依附的两个顶点，确定两个顶点的序号i和j，建立边节点，将此边节点分别插入到vi和vj对应的两个边链表的头部）
②BFS广度优先遍历
从某一顶点出发，首先依次访问该顶点的所有邻接节点，再依次访问该节点邻接节点的所有临街节点，直到所有节点被访问

①输入第一个数为根节点，之后输入的数如果小则做为左孩子（lchild）,大则做为右孩子直到输入为-1，结束构造
②在二叉树中查找关键数key时，若二叉树T=NULL，查找失败；
若key=T->data.key，查找成功；
若keydata.key，则查找T所在节点的左子树；
若key>T->data.key，则查找T所在节点的右子树

4） 数据输出（贴图：程序运行结果截图。图幅大小适当，不能太大）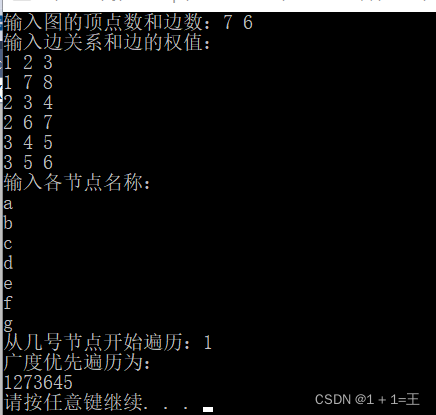

三、 实验环境

1. 操作系统：WINDOWS 10
2. 开发工具：VC++ 2013
3. 实验设备：PC

源代码（C++实现）

图的广度优先搜索

#include<iostream>#include<stdio.h>
using namespace std;#define MaxVerNum 100#define MAX_QUEUE_LENGTH 100
bool visited[MaxVerNum];typedefchar VertexType;typedefstruct VNode
{
    VertexType data;
    ArcNode * firstarc;}VNode,AdjList[MaxVerNum];typedefstruct ArcNode
{int adjvex;struct ArcNode * nextarc;int info;}ArcNode;typedefstruct{
    AdjList vertices;int vexnum, arcnum;}ALGraph;#define MAX_QUEUE_LENGTH 64     // 队列最大长度// 环形队列typedefstruct Queue{int buffer[MAX_QUEUE_LENGTH];// 队列缓冲区int begin;// 开始位置int end;// 结束位置int length;// 队列长度}Queue;voidCreateALGraph(ALGraph &G);intLocateVex(ALGraph G, VertexType v);intNextAdjVex(ALGraph G,int u,int w);voidInitQueue(Queue* pQ);intEnQueue(Queue* pQ,int Elem);intDeQueue(Queue* pQ);intQueueEmpty(Queue* pQ);voidBFS(ALGraph G,int v);intmain(){int n;
    cin >> n;
    ALGraph graph;CreateALGraph(graph);BFS(graph, n);system("pause");return0;}/*
*建立无向图的邻接表存储
*/voidCreateALGraph(ALGraph &G){int i, j, k;
    VertexType v1, v2;
    cout <<"输入顶点数和边数："<< endl;
    cin >> G.vexnum >> G.arcnum;
    cout <<"输入顶点数据："<< endl;for(i =0; i < G.vexnum; i++){
        cin >> G.vertices[i].data;
        G.vertices[i].firstarc =NULL;}
    cout <<"输入各边关系："<< endl;for(k =0; k < G.arcnum; k++){
        cin >> v1 >> v2;
        i =LocateVex(G, v1);
        j =LocateVex(G, v2);

        ArcNode *p1 = new ArcNode;
        p1->adjvex = j;
        p1->nextarc = G.vertices[i].firstarc;
        G.vertices[i].firstarc = p1;
        ArcNode *p2 = new ArcNode;
        p1->adjvex = i;
        p1->nextarc = G.vertices[j].firstarc;
        G.vertices[j].firstarc = p2;}}/*
确定顶点号
*/intLocateVex(ALGraph G, VertexType v){for(int i =0; i < G.vexnum; i++){if(v == G.vertices[i].data)return i;return-1;}}/*
功能：
初始化队列。

参数：
pQ -- 队列指针
*/voidInitQueue(Queue* pQ){
    pQ->begin = pQ->end =0;
    pQ->length =0;}/*
功能：
将元素插入队尾。

参数：
pQ -- 队列指针
Elem -- 入队的元素

返回值：
如果插入成功返回入队元素的值。
如果插入失败返回 -1。
*/intEnQueue(Queue* pQ,int Elem){//// 队列满，入队失败。//if(MAX_QUEUE_LENGTH == pQ->length)return-1;

    pQ->buffer[pQ->end]= Elem;
    pQ->end =(pQ->end +1)% MAX_QUEUE_LENGTH;
    pQ->length++;return Elem;}/*
功能：
将队首元素出队

参数：
pQ -- 队列指针

返回值：
如果出队成功返回出队元素的值。
如果出队失败返回 -1。
*/intDeQueue(Queue* pQ,int Elem){//// 队列空，出队失败//    if(QueueEmpty(pQ))return-1;

    Elem = pQ->buffer[pQ->begin];
    pQ->begin =(pQ->begin +1)% MAX_QUEUE_LENGTH;
    pQ->length--;return Elem;}/*
功能：
判断队列是否为空。

参数：
pQ -- 队列指针

返回值：
如果队列空返回 1（真）
如果队列非空返回 0（假）
*/intQueueEmpty(Queue* pQ){return0== pQ->length ?1:0;}/*
BFS广度优先遍历
*/voidBFS(ALGraph G,int v){for(int i =0; i < G.vexnum; i++){
        visited[i]= false;}
    cout << v;
    visited[v]= true;
    Queue* Q;InitQueue(Q);EnQueue(Q, v);int u;while(!QueueEmpty(Q)){DeQueue(Q,u);for(int w = v; w >=0; w =NextAdjVex(G, u, w)){if(!visited[w]){
                cout << w;
                visited[w]= true;EnQueue(Q, w);}}}}/*
下一条边
*/intNextAdjVex(ALGraph G,int u,int w){
    ArcNode *p;
    p->adjvex = u;
    w = p->nextarc->adjvex;}

二叉排序树BFS的构造

#include<iostream>

using namespace std;typedefint KeyType;// 关键码字段类型typedefstruct BinSearchNode{
    KeyType Key;// 节点的关键码字段struct BinSearchNode* lchild;// 左孩子指针struct BinSearchNode* rchild;// 右孩子指针}BinSearchNode,*BinSearchTree;

bool Tree_Search(BinSearchTree T, KeyType key);
BinSearchTree Tree_Insert(BinSearchTree T,int key);
BinSearchTree Create(BinSearchTree T);voidMiddleTravel(BinSearchTree);intmain(){
    BinSearchTree pTree=NULL;// 二叉排序树指针Create(pTree);MiddleTravel(pTree);system("pause");return0;}/*
寻找当前节点
*/
bool Tree_Search(BinSearchTree T, KeyType key){
    BinSearchTree p;
    p = T;while(p){if(key == p->Key)return true;else
            p =(key < p->Key)?(p->lchild):(p->rchild);}return false;}/*
比较关键数大小
*/
BinSearchTree Tree_Insert(BinSearchTree T,int key){
    BinSearchTree p=T;
    BinSearchTree f=NULL, s;while(p !=NULL){
        f = p;if(key == p->Key)return T;
        p =(key < p->Key)?(p->lchild):(p->rchild);}
    s = new BinSearchNode;
    s->Key = key;
    s->lchild =NULL;
    s->rchild =NULL;if(T ==NULL)return s;if(key < f->Key)
        f->lchild = s;else
        f->rchild = s;return T;}/*
创建树
*/
BinSearchTree Create(BinSearchTree T){
    KeyType key;
    T =NULL;
    cout <<"输入节点关键数，以-1结束"<< endl;
    cin >> key;while(key !=-1){Tree_Insert(T, key);
        cin >> key;}return T;}/*
中序遍历
*/voidMiddleTravel(BinSearchTree T){
    cout <<"中序遍历为：";if(T !=NULL){MiddleTravel(T->lchild);
        cout << T->Key;MiddleTravel(T->rchild);}}

博客更新至专栏【课程设计实验报告】：https://blog.csdn.net/weixin_43598687/category_11640051.html