机器学习:支持向量机 (Support Vector Machine)算法原理及python实现
文章目录
SVM算法概述
支持向量机(Support Vector Machine,SVM) 是一种用于分类问题的监督算法。SVM模型将实例表示为空间中的点,将使用一条直线(超平面)分隔数据点,且是两类数据间隔(边距:超平面与最近的类点之间的距离)最大。只通过几个支持向量就确定了超平面,说明它不在乎细枝末节,所以不容易过拟合,但不能确保一定不会过拟合。可以处理复杂的非线性问题。
如图所示的几个将训练样本分开的超平面可能有很多,应选择”正中间”, 容忍性好, 鲁棒性高, 泛化能力最强。且此个超平面以最大边距将样本分开。

SVM算法python实现
1.创建样本,例中使用二维平面中的两类点来表示两种不同样本
3.542485 1.977398 -1
3.018896 2.556416 -1
7.551510 -1.580030 1
2.114999 -0.004466 -1
8.127113 1.274372 1
7.108772 -0.986906 1
8.610639 2.046708 1
2.326297 0.265213 -1
3.634009 1.730537 -1
0.341367 -0.894998 -1
3.125951 0.293251 -1
2.123252 -0.783563 -1
0.887835 -2.797792 -1
7.139979 -2.329896 1
1.696414 -1.212496 -1
8.117032 0.623493 1
8.497162 -0.266649 1
4.658191 3.507396 -1
8.197181 1.545132 1
1.208047 0.213100 -1
1.928486 -0.321870 -1
2.175808 -0.014527 -1
7.886608 0.461755 1
3.223038 -0.552392 -1
3.628502 2.190585 -1
7.407860 -0.121961 1
7.286357 0.251077 1
2.301095 -0.533988 -1
-0.232542 -0.547690 -1
3.457096 -0.082216 -1
3.023938 -0.057392 -1
8.015003 0.885325 1
8.991748 0.923154 1
7.916831 -1.781735 1
7.616862 -0.217958 1
2.450939 0.744967 -1
7.270337 -2.507834 1
1.749721 -0.961902 -1
1.803111 -0.176349 -1
8.804461 3.044301 1
1.231257 -0.568573 -1
2.074915 1.410550 -1
-0.743036 -1.736103 -1
3.536555 3.964960 -1
8.410143 0.025606 1
7.382988 -0.478764 1
6.960661 -0.245353 1
8.234460 0.701868 1
8.168618 -0.903835 1
1.534187 -0.622492 -1
9.229518 2.066088 1
7.886242 0.191813 1
2.893743 -1.643468 -1
1.870457 -1.040420 -1
5.286862 -2.358286 1
6.080573 0.418886 1
2.544314 1.714165 -1
6.016004 -3.753712 1
0.926310 -0.564359 -1
0.870296 -0.109952 -1
2.369345 1.375695 -1
1.363782 -0.254082 -1
7.279460 -0.189572 1
1.896005 0.515080 -1
8.102154 -0.603875 1
2.529893 0.662657 -1
1.963874 -0.365233 -1
8.132048 0.785914 1
8.245938 0.372366 1
6.543888 0.433164 1
-0.236713 -5.766721 -1
8.112593 0.295839 1
9.803425 1.495167 1
1.497407 -0.552916 -1
1.336267 -1.632889 -1
9.205805 -0.586480 1
1.966279 -1.840439 -1
8.398012 1.584918 1
7.239953 -1.764292 1
7.556201 0.241185 1
9.015509 0.345019 1
8.266085 -0.230977 1
8.545620 2.788799 1
9.295969 1.346332 1
2.404234 0.570278 -1
2.037772 0.021919 -1
1.727631 -0.453143 -1
1.979395 -0.050773 -1
8.092288 -1.372433 1
1.667645 0.239204 -1
9.854303 1.365116 1
7.921057 -1.327587 1
8.500757 1.492372 1
1.339746 -0.291183 -1
3.107511 0.758367 -1
2.609525 0.902979 -1
3.263585 1.367898 -1
2.912122 -0.202359 -1
1.731786 0.589096 -1
2.387003 1.573131 -1
2.处理数据集方法,每条数据的前两个数据为坐标,最后为类别
defloadDataSet(fileName):
dataMat =[]
labelMat =[]withopen(fileName)as fr:for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2]))return dataMat, labelMat
3.主方法代码
defsmoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin',0)):"""
输入:数据集, 类别标签, 常数C, 容错率, 最大循环次数
输出:目标b, 参数alphas
"""
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler)
iterr =0
entireSet =True
alphaPairsChanged =0while(iterr < maxIter)and((alphaPairsChanged >0)or(entireSet)):
alphaPairsChanged =0if entireSet:for i inrange(oS.m):
alphaPairsChanged += innerL(i, oS)# print("fullSet, iter: %d i:%d, pairs changed %d" % (iterr, i, alphaPairsChanged))
iterr +=1else:
nonBoundIs = nonzero((oS.alphas.A >0)*(oS.alphas.A < C))[0]for i in nonBoundIs:
alphaPairsChanged += innerL(i, oS)# print("non-bound, iter: %d i:%d, pairs changed %d" % (iterr, i, alphaPairsChanged))
iterr +=1if entireSet:
entireSet =Falseelif(alphaPairsChanged ==0):
entireSet =True# print("iteration number: %d" % iterr)return oS.b, oS.alphas
defcalcWs(alphas, dataArr, classLabels):"""
输入:alphas, 数据集, 类别标签
输出:目标w
"""
X = mat(dataArr)
labelMat = mat(classLabels).transpose()
m, n = shape(X)
w = zeros((n,1))for i inrange(m):
w += multiply(alphas[i]* labelMat[i], X[i,:].T)return w
4.完整代码
from numpy import*import matplotlib.pyplot as plt
import operator
import time
#处理数据集defloadDataSet(fileName):
dataMat =[]
labelMat =[]withopen(fileName)as fr:for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2]))return dataMat, labelMat
defselectJrand(i, m):
j = i
while(j == i):
j =int(random.uniform(0, m))return j
defclipAlpha(aj, H, L):if aj > H:
aj = H
if L > aj:
aj = L
return aj
classoptStruct:def__init__(self, dataMatIn, classLabels, C, toler):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = shape(dataMatIn)[0]
self.alphas = mat(zeros((self.m,1)))
self.b =0
self.eCache = mat(zeros((self.m,2)))defcalcEk(oS, k):
fXk =float(multiply(oS.alphas, oS.labelMat).T *(oS.X * oS.X[k,:].T))+ oS.b
Ek = fXk -float(oS.labelMat[k])return Ek
defselectJ(i, oS, Ei):
maxK =-1
maxDeltaE =0
Ej =0
oS.eCache[i]=[1, Ei]
validEcacheList = nonzero(oS.eCache[:,0].A)[0]if(len(validEcacheList))>1:for k in validEcacheList:if k == i:continue
Ek = calcEk(oS, k)
deltaE =abs(Ei - Ek)if(deltaE > maxDeltaE):
maxK = k
maxDeltaE = deltaE
Ej = Ek
return maxK, Ej
else:
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)return j, Ej
defupdateEk(oS, k):
Ek = calcEk(oS, k)
oS.eCache[k]=[1, Ek]definnerL(i, oS):
Ei = calcEk(oS, i)if((oS.labelMat[i]* Ei <-oS.tol)and(oS.alphas[i]< oS.C))or((oS.labelMat[i]* Ei > oS.tol)and(oS.alphas[i]>0)):
j, Ej = selectJ(i, oS, Ei)
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()if(oS.labelMat[i]!= oS.labelMat[j]):
L =max(0, oS.alphas[j]- oS.alphas[i])
H =min(oS.C, oS.C + oS.alphas[j]- oS.alphas[i])else:
L =max(0, oS.alphas[j]+ oS.alphas[i]- oS.C)
H =min(oS.C, oS.alphas[j]+ oS.alphas[i])if(L == H):# print("L == H")return0
eta =2.0* oS.X[i,:]* oS.X[j,:].T - oS.X[i,:]* oS.X[i,:].T - oS.X[j,:]* oS.X[j,:].T
if eta >=0:# print("eta >= 0")return0
oS.alphas[j]-= oS.labelMat[j]*(Ei - Ej)/ eta
oS.alphas[j]= clipAlpha(oS.alphas[j], H, L)
updateEk(oS, j)if(abs(oS.alphas[j]- alphaJold)<0.00001):# print("j not moving enough")return0
oS.alphas[i]+= oS.labelMat[j]* oS.labelMat[i]*(alphaJold - oS.alphas[j])
updateEk(oS, i)
b1 = oS.b - Ei - oS.labelMat[i]*(oS.alphas[i]- alphaIold)* oS.X[i,:]* oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]- alphaJold)* oS.X[i,:]* oS.X[j,:].T
b2 = oS.b - Ei - oS.labelMat[i]*(oS.alphas[i]- alphaIold)* oS.X[i,:]* oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]- alphaJold)* oS.X[j,:]* oS.X[j,:].T
if(0< oS.alphas[i])and(oS.C > oS.alphas[i]):
oS.b = b1
elif(0< oS.alphas[j])and(oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b =(b1 + b2)/2.0return1else:return0defsmoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin',0)):"""
输入:数据集, 类别标签, 常数C, 容错率, 最大循环次数
输出:目标b, 参数alphas
"""
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler)
iterr =0
entireSet =True
alphaPairsChanged =0while(iterr < maxIter)and((alphaPairsChanged >0)or(entireSet)):
alphaPairsChanged =0if entireSet:for i inrange(oS.m):
alphaPairsChanged += innerL(i, oS)# print("fullSet, iter: %d i:%d, pairs changed %d" % (iterr, i, alphaPairsChanged))
iterr +=1else:
nonBoundIs = nonzero((oS.alphas.A >0)*(oS.alphas.A < C))[0]for i in nonBoundIs:
alphaPairsChanged += innerL(i, oS)# print("non-bound, iter: %d i:%d, pairs changed %d" % (iterr, i, alphaPairsChanged))
iterr +=1if entireSet:
entireSet =Falseelif(alphaPairsChanged ==0):
entireSet =True# print("iteration number: %d" % iterr)return oS.b, oS.alphas
defcalcWs(alphas, dataArr, classLabels):"""
输入:alphas, 数据集, 类别标签
输出:目标w
"""
X = mat(dataArr)
labelMat = mat(classLabels).transpose()
m, n = shape(X)
w = zeros((n,1))for i inrange(m):
w += multiply(alphas[i]* labelMat[i], X[i,:].T)return w
defplotFeature(dataMat, labelMat, weights, b):
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 =[]; ycord1 =[]
xcord2 =[]; ycord2 =[]for i inrange(n):ifint(labelMat[i])==1:
xcord1.append(dataArr[i,0])
ycord1.append(dataArr[i,1])else:
xcord2.append(dataArr[i,0])
ycord2.append(dataArr[i,1])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = arange(2,7.0,0.1)
y =(-b[0,0]* x)-10/ linalg.norm(weights)
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2')
plt.show()#调用函数defmain():#数据集初始化
trainDataSet, trainLabel = loadDataSet('SVMSet.txt')
b, alphas = smoP(trainDataSet, trainLabel,0.6,0.0001,40)
ws = calcWs(alphas, trainDataSet, trainLabel)print("ws = \n", ws)print("b = \n", b)
plotFeature(trainDataSet, trainLabel, ws, b)if __name__ =='__main__':
start = time.perf_counter()
main()
end = time.perf_counter()print('finish all in %s'%str(end - start))
运行结果
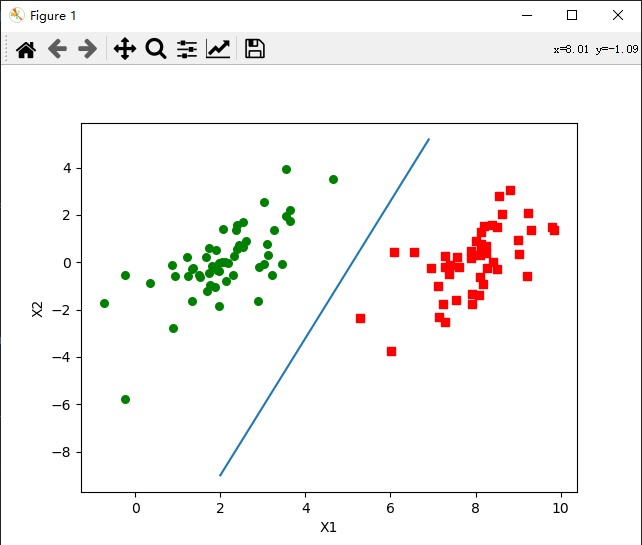
可见此次svm分类方法分类效果较好,可以较好地分割样本
SVM 算法特性
1.训练好的模型的算法复杂度是由支持向量的个数决定的,而不是由数据的维度决定的。所以 SVM 不太容易产生 overfitting。
2.SVM 训练出来的模型完全依赖于支持向量,即使训练集里面所有非支持向量的点都被去除,重复训练过程,结果仍然会得到完全一样的模型。
3.一个 SVM 如果训练得出的支持向量个数比较少,那么SVM 训练出的模型比较容易被泛化。
版权归原作者 目标四级424 所有, 如有侵权,请联系我们删除。