0
0

【Python算法】数值分析—列主元高斯消元法——附源码

一、背景

\left\{\begin{matrix}a_{11} x_{1} + a_{12} x_{2} + \dots a_{1n} x_{n} = b_{1} \\a_{21} x_{1} + a_{22} x_{2} + \dots a_{2n} x_{n} = b_{2} \\\dots \\a_{n1} x_{1} + a_{n2} x_{2} + \dots a_{nn} x_{n} = b_{n} \end{matrix}\right.

    线性方程组有很多种解法，可以最简单的直接代入消元计算，但是运算量较大，且过程复杂不直观。

    高斯消元法目的是预处理方程组的系数矩阵，将系数矩阵变换为上三角矩阵，这样整个方程就变得清晰直观很多，即使不借助计算机，也是可以很简单的手算出结果。

    **原方程**：

\begin{bmatrix} a_{11} &a_{12} &a_{13} & \dots &a_{1n} \\a_{21} &a_{22} &a_{23} & \dots &a_{2n} \\a_{31} &a_{32} &a_{33} & \dots &a_{3n} \\a_{41} &a_{42} &a_{43} & \dots &a_{4n} \\\vdots &\vdots & \vdots &\ddots &\vdots \\a_{n1} &a_{n2} &a_{n3} & \dots &a_{nn} \end{bmatrix} \begin{bmatrix}x_{1} \\x_{2} \\x_{3} \\x_{4} \\\vdots \\x_{n} \end{bmatrix}= \begin{bmatrix}b_{1} \\b_{2} \\b_{3} \\b_{4} \\\vdots \\b_{n} \end{bmatrix}

    **高斯消元后的方程**，这样最下行的方程只是一个简单的一元一次方程，倒数第二行是二元一次，依次倒着求解，整个过程变得清晰直观。（全部元素带撇“ ' ”， 是因为消元涉及大量的对换两行元素的运算，所以方程的书写顺序是在不断被改变的，只是为了保持美观和一致，仍采用下标1234n的写法）

\begin{bmatrix} a^{'}_{11} &a^{'}_{12} &a^{'}_{13} & \dots &a^{'}_{1n-1} &a^{'}_{1n} \\0 &a^{'} _{22} &a^{'}_{23} & \dots &a^{'}_{2n-1} &a^{'}_{2n} \\0 &0 &a^{'}_{33} & \dots &a^{'}_{3n-1} &a^{'}_{3n} \\0 &0 &0 & \dots &a^{'}_{4n-1} &a^{'}_{4n} \\\vdots &\vdots & \vdots &\ddots &\vdots & \vdots \\0 &0 &0 & \dots &0 &a^{'}_{nn} \end{bmatrix} \begin{bmatrix}x^{'}_{1} \\x^{'}_{2} \\x^{'}_{3} \\x^{'}_{4} \\\vdots \\x^{'}_{n} \end{bmatrix}= \begin{bmatrix}b^{'}_{1} \\b^{'}_{2} \\b^{'}_{3} \\b^{'}_{4} \\\vdots \\b^{'}_{n} \end{bmatrix}

    而**列主元高斯消元法**，是为了克服高斯消元法的”**除法bug**“的改进版本， 因为消元过程中用到了除法，对于计算机来说，**如果一个很小的值作为分母，则其在迭代中产生的误差，在做除法后会被放大很多倍**。如0.0001与0.0002的误差小，但是1/0.0001与1/0.0002的误差巨大。列主元思想，就顺应而生，在消元前，把列中最大的元素所在行放到矩阵的最上方，那么就可以让较大值做分母，从而避免了误差被除法放大的问题。

二、方法逻辑（function文件，完整代码在文末）

1.寻找一列中的最大元素，并返回其所在行数

def get_max_row_in_column(matrix_a, j):
    """ 获取第j列中最大元素的所在行数
     此方法将被反复调用，所以每次运算时，不是从整个系数矩阵a中找最大行数，
     而是从可能已经做过几次消元的系数矩阵a的(j, j)子矩阵(尚未进行消元操作的部分)中寻找最大行数 """
    max_item = abs(matrix_a[j][j])
    max_row = j
    for i in list(range(j, matrix_a.shape[0])):
        if abs(matrix_a[i][j]) > abs(max_item):
            max_item = matrix_a[i][j]
            max_row = i
    return max_row

2.交换系数矩阵a的两行元素

def swap_row_in_matrix_a(matrix_a, max_row, i):
    """ 在系数矩阵a中交换某两行的元素 """
    for j in (list(range(i, matrix_a.shape[1]))):
        temp = matrix_a[i][j]
        matrix_a[i][j] = matrix_a[max_row][j]
        matrix_a[max_row][j] = temp

3.交换值矩阵b的两行元素

def swap_row_in_matrix_b(matrix_b, max_row, i):
    """ 在值矩阵b中交换某两行的元素 """
    temp = matrix_b[i][0]
    matrix_b[i][0] = matrix_b[max_row][0]
    matrix_b[max_row][0] = temp

4.高斯消元法主循环

def method_elimination_gauss(matrix_a, matrix_b):
    """ 高斯消元法主循环 """
    for i in list(range(0, matrix_a.shape[0])):  # 逐行处理矩阵数据
        max_row = get_max_row_in_column(matrix_a, i)  # 在当前系数矩阵的(i, i)子矩阵中获取第一列中最大元素所在行数，准备进行交换
        swap_row_in_matrix_a(matrix_a, max_row, i)  # 将最大元素所在行数交换至(i, i)子矩阵的第一行
        swap_row_in_matrix_b(matrix_b, max_row, i)  # 同时交换值矩阵b的元素，使方程的系数与值保持对应关系

        for k in list(range(i + 1, matrix_a.shape[0])):
            if matrix_a[i][i] != 0:  # 此时从系数矩阵的(i, i)子矩阵中获取的[i][i]元素已经是该列中绝对值最大的数，若为0，则奇异
                scale_factor = (-matrix_a[k][i]/matrix_a[i][i])  # 计算接下来消元需要用到的比例因子
            else:
                print('该矩阵奇异，无法求解方程组')
                sys.exit(0)

            for j in list(range(i, matrix_a.shape[1])):
                matrix_a[k][j] = scale_factor * matrix_a[i][j] + matrix_a[k][j]  # 消元，高斯消元法的核心之处
            matrix_b[k][0] = scale_factor * matrix_b[i] + matrix_b[k][0]  # 对b进行同样的”消元“

5.在上三角方程的基础上求解方程

def solve_equation(matrix_a, matrix_b):
    """ 求解消元后的上三角方程 """
    x = np.zeros((matrix_a.shape[0], 1))
    if matrix_a[-1][-1] != 0:
        x[-1] = matrix_b[-1] / matrix_a[-1][-1]
    else:  # 若此上三角方程的系数矩阵的最后一行最后一列元素为0，说明矩阵奇异，无数解
        print('该矩阵奇异，无法求解方程组')
        sys.exit(0)  # 强制退出

    for i in list(range(matrix_a.shape[0] - 2, -1, -1)):  # 从上三角方程最后一行开始解方程，倒着计算
        sum_a = 0
        for j in list(range(i + 1, matrix_a.shape[0])):
            sum_a += matrix_a[i][j] * x[j]
        x[i] = (matrix_b[i] - sum_a) / matrix_a[i][i]
    return x

三、最终实现（main文件，完整代码）

import numpy as np
import function as fun

# 为保证程序的连续性，一下两个矩阵均采用numpy库的矩阵形式输入，而不以数组形式输入
# 方程的系数矩阵a
matrix_a = np.array([[0.4096, 0.1234, 0.3678, 0.2943],
                     [0.2246, 0.3872, 0.4015, 0.1129],
                     [0.3645, 0.1920, 0.3781, 0.0643],
                     [0.1784, 0.4002, 0.2786, 0.3927]])
# 方程的值矩阵b
matrix_b = np.array([[1.1951],
                    [1.1262],
                    [0.9989],
                    [1.2499]])

# 输出结果
print("原系数矩阵a:")
print(matrix_a, "\n")
print("原值矩阵b:")
print(matrix_b, "\n")
fun.method_elimination_gauss(matrix_a, matrix_b)
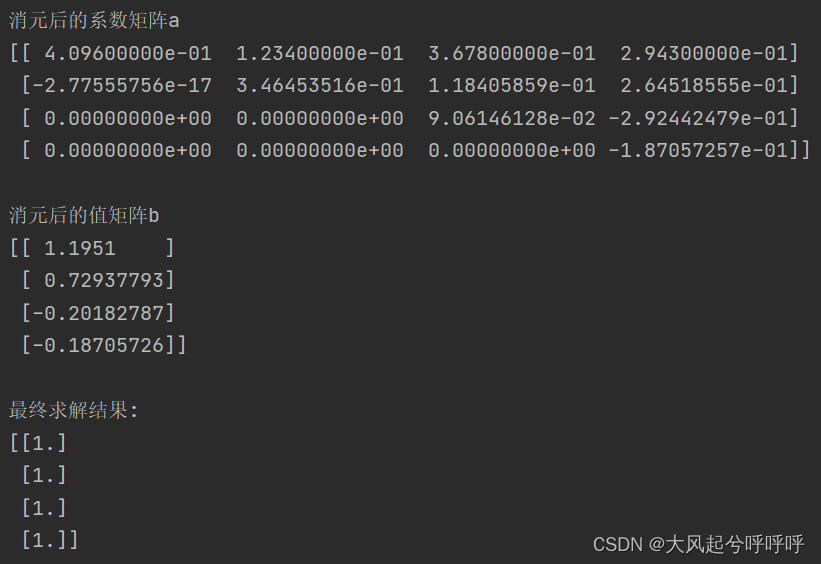
print("消元后的系数矩阵a")
print(matrix_a, "\n")
print("消元后的值矩阵b")
print(matrix_b, "\n")
print("最终求解结果:")
print(fun.solve_equation(matrix_a, matrix_b))

测试结果：

function文件完整代码

import sys
import numpy as np

def get_max_row_in_column(matrix_a, j):
    """ 获取第j列中最大元素的所在行数
     此方法将被反复调用，所以每次运算时，不是从整个系数矩阵a中找最大行数，
     而是从可能已经做过几次消元的系数矩阵a的(j, j)子矩阵(尚未进行消元操作的部分)中寻找最大行数 """
    max_item = abs(matrix_a[j][j])
    max_row = j
    for i in list(range(j, matrix_a.shape[0])):
        if abs(matrix_a[i][j]) > abs(max_item):
            max_item = matrix_a[i][j]
            max_row = i
    return max_row

def swap_row_in_matrix_a(matrix_a, max_row, i):
    """ 在系数矩阵a中交换某两行的元素 """
    for j in (list(range(i, matrix_a.shape[1]))):
        temp = matrix_a[i][j]
        matrix_a[i][j] = matrix_a[max_row][j]
        matrix_a[max_row][j] = temp

def swap_row_in_matrix_b(matrix_b, max_row, i):
    """ 在值矩阵b中交换某两行的元素 """
    temp = matrix_b[i][0]
    matrix_b[i][0] = matrix_b[max_row][0]
    matrix_b[max_row][0] = temp

def method_elimination_gauss(matrix_a, matrix_b):
    """ 高斯消元法主循环 """
    for i in list(range(0, matrix_a.shape[0])):  # 逐行处理矩阵数据
        max_row = get_max_row_in_column(matrix_a, i)  # 在当前系数矩阵的(i, i)子矩阵中获取第一列中最大元素所在行数，准备进行交换
        swap_row_in_matrix_a(matrix_a, max_row, i)  # 将最大元素所在行数交换至(i, i)子矩阵的第一行
        swap_row_in_matrix_b(matrix_b, max_row, i)  # 同时交换值矩阵b的元素，使方程的系数与值保持对应关系

        for k in list(range(i + 1, matrix_a.shape[0])):
            if matrix_a[i][i] != 0:  # 此时从系数矩阵的(i, i)子矩阵中获取的[i][i]元素已经是该列中绝对值最大的数，若为0，则奇异
                scale_factor = (-matrix_a[k][i]/matrix_a[i][i])  # 计算接下来消元需要用到的比例因子
            else:
                print('该矩阵奇异，无法求解方程组')
                sys.exit(0)

            for j in list(range(i, matrix_a.shape[1])):
                matrix_a[k][j] = scale_factor * matrix_a[i][j] + matrix_a[k][j]  # 消元，高斯消元法的核心之处
            matrix_b[k][0] = scale_factor * matrix_b[i] + matrix_b[k][0]  # 对b进行同样的”消元“

def solve_equation(matrix_a, matrix_b):
    """ 求解消元后的上三角方程 """
    x = np.zeros((matrix_a.shape[0], 1))
    if matrix_a[-1][-1] != 0:
        x[-1] = matrix_b[-1] / matrix_a[-1][-1]
    else:  # 若此上三角方程的系数矩阵的最后一行最后一列元素为0，说明矩阵奇异，无数解
        print('该矩阵奇异，无法求解方程组')
        sys.exit(0)  # 强制退出

    for i in list(range(matrix_a.shape[0] - 2, -1, -1)):  # 从上三角方程最后一行开始解方程，倒着计算
        sum_a = 0
        for j in list(range(i + 1, matrix_a.shape[0])):
            sum_a += matrix_a[i][j] * x[j]
        x[i] = (matrix_b[i] - sum_a) / matrix_a[i][i]
    return x

demo源码链接如下

github地址：https://github.com/method_elimination_gauss

gitee地址：https://gitee.com/darlingxyz/method_elimination_gauss

标签： python 算法 pycharm
本文转载自: https://blog.csdn.net/qq_50920297/article/details/124221473
版权归原作者 大风起兮呼呼呼 所有， 如有侵权，请联系我们删除。
登录后发布评论

“【Python算法】数值分析—列主元高斯消元法——附源码”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

泷羽sec-星光不负a-学习打卡-安全见闻(1)

Linux 经典面试八股文

docker 拉取MySQL8.0镜像以及安装

【PowerShell】如何使用Pester进行单元测试？

PyCharm中TensorFlow安装指南及.whl文件使用

移动UI：意见反馈设计的8大要点，让用户和产品畅快沟通。

git | 删除指定 commit

文章导航