【机器学习】吴恩达作业2.0，python实现线性可分logistic逻辑回归

2.0 Logistic回归模型 (线性可分)

预测一个学生是否被大学录取。假设你是大学某个院系的管理员，你想通过申请人在两门考试中的表现来决定每个人的录取率，你有来自以前申请人的历史数据，你可以用这些数据作为训练集建立Logistic回归，对每一个训练样本，你有申请人在两门考试中的分数和录取决定。
建立一个分类模型，基于这两门课的分数来估计申请人的录取概率。

https://blog.csdn.net/weixin_44750583/article/details/88377195

线性可分

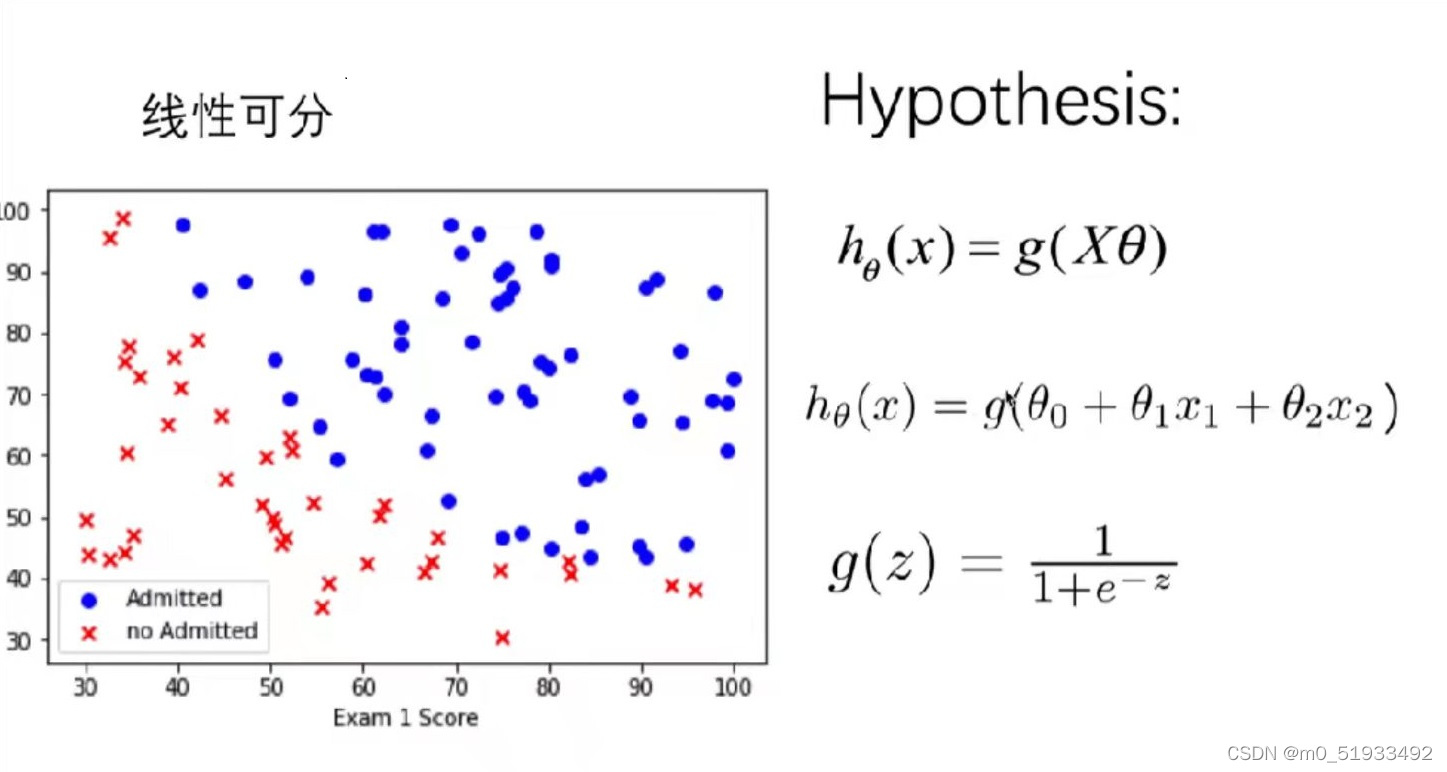
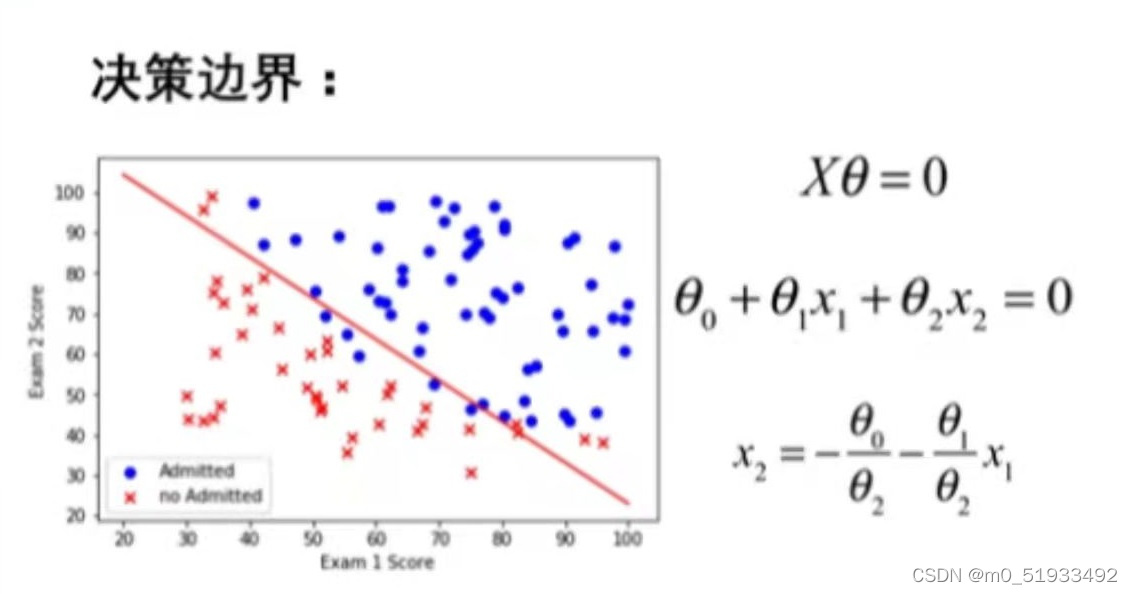
决策边界：

损失函数

梯度下降

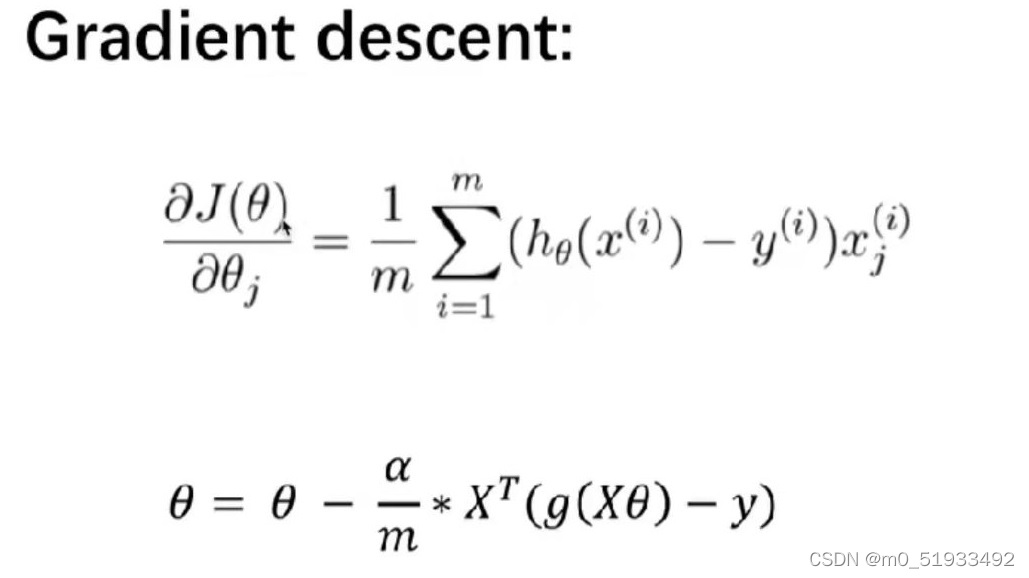
Python语法

1 Pandas 中使用 iloc 函数 进行数据切片
方法名称说明.loc[]基于标签索引选取数据.iloc[]基于整数索引选取数据
2 将dataframe->ndarray:

(1)df.values

(2)df.as_matrix()

(3)np.array(df)

3 DataFrame.insert(loc, column, value, allow_duplicates=False)[source]

loc:插入的列索引 。 column:插入列的标签 ，字符串。 value 插入列的值。

维度

X（m,n）y(m,1) theta(n,1)

代码

1.读取数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt

#1.读取数据
path = 'ex2data1.txt'
data = pd.read_csv(path, names=['Exam1', 'Exam2', 'Accepted'])#读取数据
data.head()#显示数据前五行

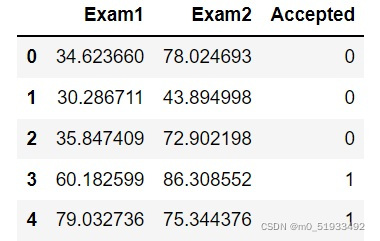
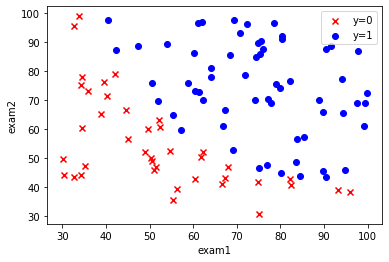
2.可视化数据集

#2.可视化数据集
fig, ax = plt.subplots()#此句显示图像
ax.scatter(data[data['Accepted'] == 0]['Exam1'], data[data['Accepted'] == 0]['Exam2'], c='r', marker='x', label='y=0')
ax.scatter(data[data['Accepted'] == 1]['Exam1'], data[data['Accepted'] == 1]['Exam2'], c='b', marker='o', label='y=1')
ax.legend()#显示标签
ax.set_xlabel('exam1')#设置坐标轴标签
ax.set_ylabel('exam2')

plt.show()

def get_Xy(data):
    # 在第一列插入1
    data.insert(0, 'ones', 1)
    # 取除最后一列以外的列
    X_ = data.iloc[:, 0:-1]
    # 取特征值
    X = X_.values
    # 取最后一列
    y_ = data.iloc[:, -1]
    y = y_.values.reshape(len(y_), 1)
    return X, y

X, y = get_Xy(data)
print(X)
print(y)
# (100,3)
print(X.shape)
# （100，1）
print(y.shape)

** 3.损失函数**

#3.损失函数
#sigmoid函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def Cost_Function(X, y, theta):
    A = sigmoid(X @ theta)
    first = y * np.log(A)
    second = (1 - y) * np.log(1 - A)
    return -np.sum(first + second) / len(X)

theta = np.zeros((3, 1))#初始化theta
print(theta.shape)
cost_init = Cost_Function(X, y, theta)
print(cost_init)

** 4.梯度下降**

#4.梯度下降
def gradientDescent(X, y, theta, alpha, iters):
    m = len(X)
    costs = []
    for i in range(iters):
        A = sigmoid(X @ theta)
        # X.T:X的转置
        theta = theta - (alpha / m) * X.T @ (A - y)
        cost = Cost_Function(X, y, theta)#计算每次迭代损失
        costs.append(cost)#总损失
        # if i % 1000 == 0:
        #     print(cost)
    return costs, theta

#初始化参数
alpha = 0.004
iters = 200000
costs, theta_final = gradientDescent(X, y, theta, alpha, iters)#梯度下降完得到的参数theta和损失
print(theta_final)

** 5.预测**

#5.预测
def predict(X, theta):
    prob = sigmoid(X @ theta)#逻辑回归的假设函数
    return [1 if x >= 0.5 else 0 for x in prob]

print(predict(X, theta_final))

y_ = np.array(predict(X, theta_final))#将预测结果转换为数组
print(y_)#打印预测结果
y_pre = y_.reshape(len(y_), 1)#将预测结果转换为一列

# 预测准确率
acc = np.mean(y_pre == y)
print(acc)#0.86

关于预测准确率：

# 例 1
x = [1, 0, 1, 1, 1, 1]
y = [0, 0, 0, 0, 0, 1]
print(x == y)
结果：
False
# 例 2
x = np.array([1, 0, 1, 1, 1, 1])
y = np.array([0, 0, 0, 0, 0, 1])
print(x == y)
结果：
[False True False False False True]
# 例 3
x = np.array([1, 0, 1, 1, 1, 1])
y = np.array([0, 0, 0, 0, 0, 1])
print("{:.2f}".format(np.mean(x == y)))
结果：
0.33

说明：
1、 x == y表示两个数组中的值相同时，输出True；否则输出False
2、例3对例2中结果取平均值，其中True=1,False=0;

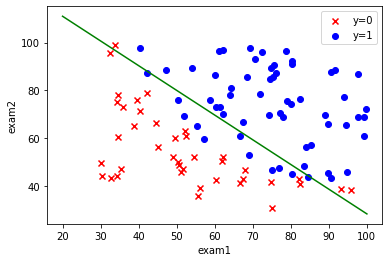
** 6.可视化决策边界**

#6.决策边界
# 决策边界就是Xθ=0的时候
coef1 = - theta_final[0, 0] / theta_final[2, 0]
coef2 = - theta_final[1, 0] / theta_final[2, 0]
x = np.linspace(20, 100, 100)
f = coef1 + coef2 * x
fig, ax = plt.subplots()
ax.scatter(data[data['Accepted'] == 0]['Exam1'], data[data['Accepted'] == 0]['Exam2'], c='r', marker='x', label='y=0')
ax.scatter(data[data['Accepted'] == 1]['Exam1'], data[data['Accepted'] == 1]['Exam2'], c='b', marker='o', label='y=1')
ax.legend()
ax.set_xlabel('exam1')
ax.set_ylabel('exam2')
ax.plot(x, f, c='g')
plt.show()

** 完整代码**

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt

#1.读取数据
path = 'ex2data1.txt'
data = pd.read_csv(path, names=['Exam1', 'Exam2', 'Accepted'])#读取数据
data.head()#显示数据前五行

#2.可视化数据集
fig, ax = plt.subplots()#此句显示图像
ax.scatter(data[data['Accepted'] == 0]['Exam1'], data[data['Accepted'] == 0]['Exam2'], c='r', marker='x', label='y=0')
ax.scatter(data[data['Accepted'] == 1]['Exam1'], data[data['Accepted'] == 1]['Exam2'], c='b', marker='o', label='y=1')
ax.legend()#显示标签
ax.set_xlabel('exam1')#设置坐标轴标签
ax.set_ylabel('exam2')

plt.show()

#3.损失函数
#sigmoid函数
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

def Cost_Function(X, y, theta):
    A = sigmoid(X @ theta)
    first = y * np.log(A)
    second = (1 - y) * np.log(1 - A)
    return -np.sum(first + second) / len(X)

theta = np.zeros((3, 1))#初始化theta
print(theta.shape)
cost_init = Cost_Function(X, y, theta)
print(cost_init)

#4.梯度下降
def gradientDescent(X, y, theta, alpha, iters):
    m = len(X)
    costs = []
    for i in range(iters):
        A = sigmoid(X @ theta)
        # X.T:X的转置
        theta = theta - (alpha / m) * X.T @ (A - y)
        cost = Cost_Function(X, y, theta)#计算每次迭代损失
        costs.append(cost)#总损失
        # if i % 1000 == 0:
        #     print(cost)
    return costs, theta

#初始化参数
alpha = 0.004
iters = 200000
costs, theta_final = gradientDescent(X, y, theta, alpha, iters)#梯度下降完得到的参数theta和损失
print(theta_final)

#5.预测
def predict(X, theta):
    prob = sigmoid(X @ theta)#逻辑回归的假设函数
    return [1 if x >= 0.5 else 0 for x in prob]

print(predict(X, theta_final))

y_ = np.array(predict(X, theta_final))#将预测结果转换为数组
print(y_)
y_pre = y_.reshape(len(y_), 1)

# 求取均值
acc = np.mean(y_pre == y)
print(acc)

#6.决策边界
# 决策边界就是Xθ=0的时候
coef1 = - theta_final[0, 0] / theta_final[2, 0]
coef2 = - theta_final[1, 0] / theta_final[2, 0]
x = np.linspace(20, 100, 100)
f = coef1 + coef2 * x
fig, ax = plt.subplots()
ax.scatter(data[data['Accepted'] == 0]['Exam1'], data[data['Accepted'] == 0]['Exam2'], c='r', marker='x', label='y=0')
ax.scatter(data[data['Accepted'] == 1]['Exam1'], data[data['Accepted'] == 1]['Exam2'], c='b', marker='o', label='y=1')
ax.legend()
ax.set_xlabel('exam1')
ax.set_ylabel('exam2')
ax.plot(x, f, c='g')
plt.show()

总结：

导入数据集——可视化数据集——定义损失函数——梯度下降——预测——可视化决策边界