模式识别 第7、8章 特征的选择和提取

**一、基本概念 **

1.问题的提出

特征→ 特征空间：
每一个特征对应特征空间的一个维度 ；特征越多，特征空间的维度越高

原则：在保证分类效果的前提下用尽量少的特征来完成分类

2.基本概念

（1）特征形成：由仪器直接测量出来的数值，或者是根据仪器的数据进行计算后的结果

（2）特征选择：用计算的方法从一组给定的特征中选择一部分特征进行分类

（3）特征提取：通过适当的变换把原有的D个特征转换为d（<D）个特征

3.特征选择

*一是对特征的评价*，也就是怎样衡量一组特征对分类的有效性 **

二是寻优的算法，就是怎样更快地找到性能最优或比较优的特征组合

4.特征的评价准则

**利用分类器的错误率作为准则是最直接的想法，但是不可行； ****定义与错误率有一定关系但又便于计算的类别可分性准则Jij **用来衡量在一组特征下第i类和第j类之间的可分程度

对判据的要求 ： 单调、可加、度量

**二、类别可分离性判据 **

1.常用的特征判据

1. 基于类内类间距离的可分性判据

（1）基本思想：计算各类特征向量之间的平均距离，考虑最简单的两类情况，可以用两类中任意两两样本间的平均来代表两个类之间的距离。

（2）判据的表达式：

（3）矩阵形式的类间距离的表达式

** （4）其它的基于类内类间距离的判据**

2. 基于概率分布的可分性判据

用两类分布密度函数间的距离（或重叠程度）来度量可分性， 构造基于概率分布的可分性判据

重叠程度反应了概密函数间的相似程度。

（1）定义：两个密度函数之间的距离

（2）Bhattacharyya距离（巴氏距离）

（3）Chernoff界（切诺夫界）

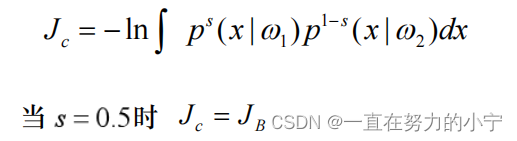
**（4）散度----**人们在似然比的基础上定义了散度来作为类别可分性的度量

3. 基于熵的可分性判据

** （1）定义：**借用熵的概念来描述各类的可分性

在特征的某个取值下： 如果样本属于各类的后验概率越平均，则该特征越不利于分类； 如果后验概率越集中于某一类，则特征越有利于分类。在信息论中，熵表示不确定性，熵越大不确定性越大

（2）思路：

（3）常用的熵度量

① Shannon熵

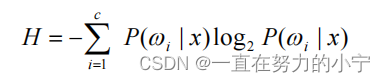
② 平方熵

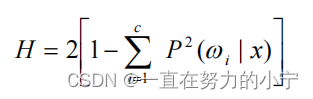
③ 基于熵的可分性判据

**三、特征选择的最优和次优算法 **

1.特征选择的最优算法

**1. **最优算法

• 最基本的方法就是穷举法，就是穷举所有这些可能，从中选择判据最优的组合

• 另外一种取得最优解的方法是分枝定界法

2. 分枝定界法（branch and bound）

• 自顶向下：从包含所有候选特征开始，逐步去掉不被选中的特征

• 回溯：考虑到所有可能的组合

• 基本思想：从左到右建树 → 从右到左搜索 → 回溯避免不必要计算 → 找到最优解

• 计算量：在d大约为D的一半时，分枝定界法比穷举法节省的计算量最大

• 算法要点：根节点为全体特征，每个结点上舍弃一个特征，各个叶结点代表选择的各种组合 等

2.特征选择的次优算法

1. 单独最优特征的组合

• 计算各特征单独使用时的判据值并加以排队，取前d 个作为选择结果。

• 这一结果与所采用的特征选择的准则函数有关，只有当所采用的判据是每个特征上的判据之和或

之积时，这种做法选择出的才是最优的特征

2. 顺序前进法

• 最简单的“自下而上”的搜索方法

• 每次从未入选的特征中选择一个特征，使得它与已入选的特征组合在一起时所得判据J值为最大，直到特征数增加到d 为止.

3. 顺序后退法

• 是一种“自上而下”的方法。

• 从全体特征开始每次剔除一个，所剔除的特征应使仍然保留的特征组的判据J值最大，直到特征数减少到d 为止

4. 增l减r法（l-r法）

在第k步可先用顺序前进法一个个加入特征到 k+l 个， 然后再用顺序后退法一个个剔去 r 个特征，我们把这样一种 算法叫增 l 减 r 法（l–r 法）

**四、特征提取之PCA算法 **

1.问题的提出

2.主成分分析PCA

主成分分析PCA是一种常用的基于变量协方差矩阵对信息进行处理、压缩和抽提的有效方法。

出发点是从一组特征中计算出一组按重要性从大到小排列的新特征，它们是原有特征的线性组合，并且相互之间是不相关的。

主成分分析的目的：压缩变量个数，用较少的变量去解释原始数据中的大部分变量，剔除冗余信息

一般来说，我们希望能用一个或少数几个综合指标（分数）来代替原来分数表做统计分析，而且希望新的综合指标能够尽可能地保留原有信息，并****具有最大的方差。

3.主成分分析的方法

• 是通过适当的变换把D个特征转换为d个新特征

• 这里的特征提取专指从一组已有的特征通过一定的数学运算得到一组新特征，有时也把这种特征提取称为特征变换

1. 计算第一主成分

ξ1称作第一主成分，它在原始特征的所有线性组合里是方差最大的

用求拉格朗日函数的极值的方法来求解新特征的系数

2. 计算第二主成分

要求：方差最大，模为1，还必须与第一主成分不相关

a2是∑的第二大本征值对应的本征向量，ξ2被称作第二主成分。

3.计算主成分的贡献率（主成分数量的确定方法）

可以事先确定希望新特征所能代表的数据总方差的比例

例如，80%或90%，根据上面的式子来试算出合适的k值。

4. 主成分分析的理解

通过构造原特征的适当的线性组合，以产生一系列互不相关的新特征,从中选出少数几个新特征并使它们含有尽可能多的原特征带有的信息，从而使得用这几个新特征代替原特征分析问题和解决问题成为可能。

5. 三维主成分分析示意图

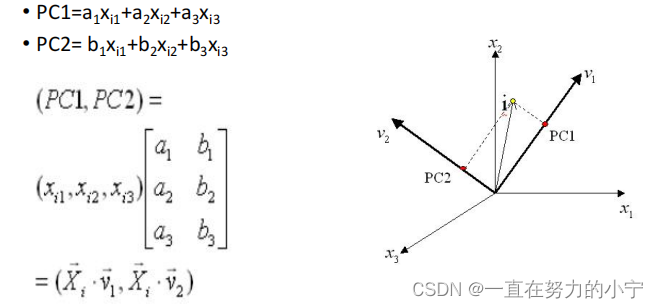
6. 总结主成分分析的步骤

7. 主成分分析方法应用举例

**主成分的特点： **

1）主成分是原变量的线性组合；

2）各个主成分之间互不相关；

3）主成分按照方差从大到小依次排列，第一主成分对应最大的方差（特征值）；

4）每个主成分的均值为0、其方差为协方差阵对应的特征值；

5）不同的主成分轴（载荷轴）之间相互正交。

**特征提取之K-L变换 **

K--L变换

1. K-L展开式

2. 均方误差

3. K-L变换与产生矩阵

4. K-L变换进行特征提取的步骤

5. 例题

两个模式类的样本分别为

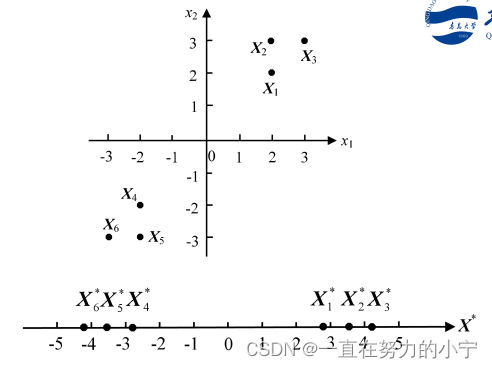
6. K-L变换与主成分分析法的对比

7.K-L变换用于监督模式识别的方法 --从类均值中提取判别信息

应用举例

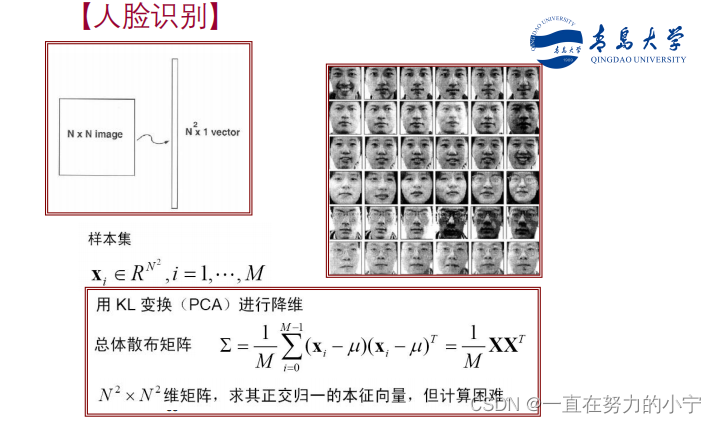
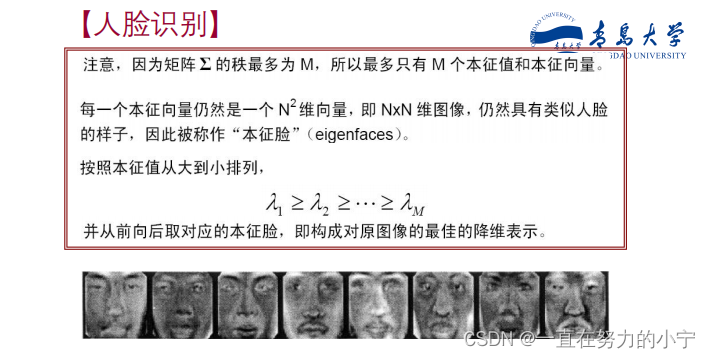
总结