这个是我个人学习笔记,跟着b站沐神学习,链接:08 线性回归 + 基础优化算法【动手学深度学习v2】_哔哩哔哩_bilibili
我仅仅对代码进行一些解读,发现有解读不对的地方,欢迎大家来评论区讨论
🎄生成数据集
🎋第一步:导包
import torch
import random
from d2l import torch as d2l
若显示报错,没有d2l这个模块,在jupyter notebook中输入
!pip install -U d2l
🎋第二步:构造函数

def synthetic_data(w,b,num_examples):
'''生成y = wx + b + 噪声。 '''
x = torch.normal(0,1,(num_examples,len(w)))
y = torch.matmul(x,w) + b
y += torch.normal(0,0.01,y.shape)
return x,y.reshape((-1,1))
true_w = torch.tensor([2,-3.4])
true_b = 4.2
features,labels = synthetic_data(true_w,true_b,1000)
print("features:",features[0],"\nlabels:",labels[0])
1)此处b是个一维向量,当matmul的第一个参数是2维向量,第2个参数是一维向量时,返回的是矩阵和向量的乘积,结果是向量,因此,y需要reshape
2)reshape中-1表示自动计算,1表示固定,即列向量为1
3)创建一个形状为(3,4)的张量。 其中的每个元素都从均值为0、标准差为1的标准高斯分布(正态分布)中随机采样。
normal(0, 1, size=(3, 4))
🎋结果

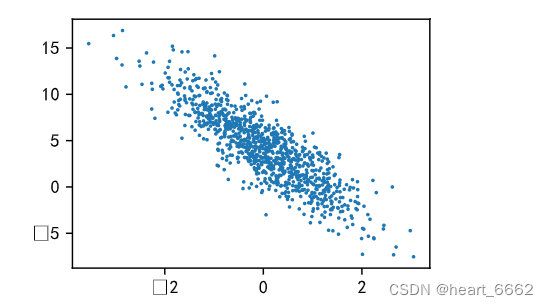
🎋第三步:画图看一下是不是线性相关
d2l.set_figsize()
d2l.plt.scatter(features[:,-1].detach().numpy(),
labels.detach().numpy(),1)
1)detach()分离出数值,不再含有梯度
2)scatter()函数最后的一个1是绘制点直径的大小,如果改成50会看到一个个点非常粗
**3)总的来说 生成第二个特征
features[:, 1]和
labels的散点图, 可以直观观察到两者之间的线性关系**
🎄读取数据集
🎋第一步:定义函数

** 训练模型时要对数据集进行遍历,每次抽取一小批量样本,并使用它们来更新我们的模型。 由于这个过程是训练机器学习算法的基础,所以有必要定义一个函数, 该函数能打乱数据集中的样本并以小批量方式获取数据。**
**在下面的代码中,我们定义一个
data_iter函数, 该函数接收批量大小、特征矩阵和标签向量作为输入,生成大小为
batch_size的小批量。 每个小批量包含一组特征和标签**
def data_iter(batch_size,features,labels):
num_examples = len(features)
indices = list(range(num_examples))
#这些样本是随机读取的,没有特定的顺序
random.shuffle(indices)
for i in range(0,num_examples,batch_size):
batch_indices = torch.tensor(
indices[i:min(i+batch_size,num_examples)])
yield features[batch_indices],labels[batch_indices]
1)只是indices这个list被打乱了,features和labels都是顺序的,用循环才能随机地放进去
2)min的作用 不让访问越界 list超出会报错,out of index
**3)通过 yield,创建生成器 **链接:【python】基础知识巩固(一)_heart_6662的博客-CSDN博客
我们不再需要编写读文件的迭代类,就可以轻松实现文件读取
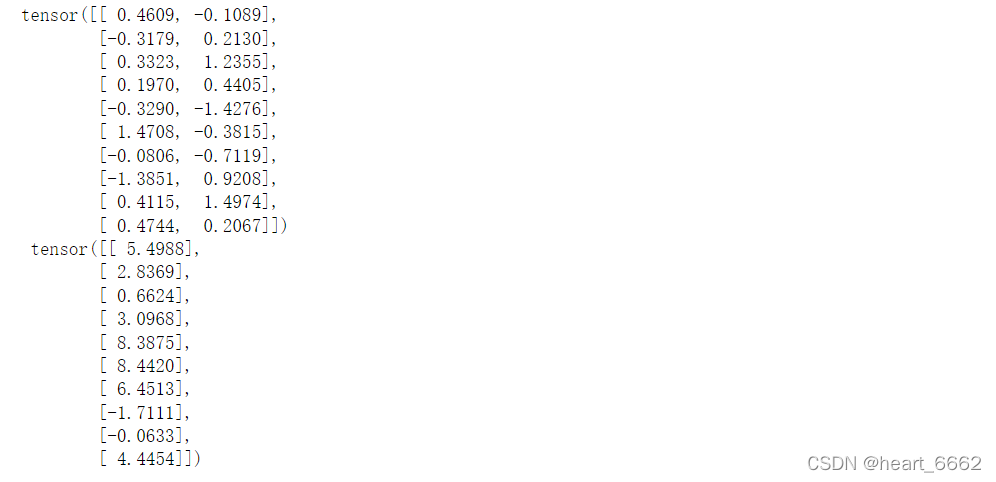
🎋第二步:感受一下小批量运算
**我们直观感受一下小批量运算:读取第一个小批量数据样本并打印。 每个批量的特征维度显示批量大小和输入特征数。 同样的,批量的标签形状与
batch_size
相等**
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, '\n', y)
break
🎄 初始化模型参数
通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重, 并将偏置初始化为0
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
**1)计算梯度**作用在于更新参数
requires_grad=True2)b为偏置 偏置初始化为0
🎄 定义模型
def linreg(X, w, b): #@save
"""线性回归模型"""
return torch.matmul(X, w) + b
1)torch.matmul(X, w) 矩阵乘以向量 等于 向量
2)b是标量
根据广播机制: 当我们用一个向量加一个标量时,标量会被加到向量的每个分量上
🎄定义损失函数
def squared_loss(y_hat, y): #@save
"""均方损失"""
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
**1)均方损失为 (预测值
y_hat 减去y真实值 )的平方 除以2**
**2)而且需要将真实值
y的形状转换为和预测值
y_hat的形状相同**
🎄定义优化算法
小批量随机梯度下降。
在每一步中,使用从数据集中随机抽取的一个小批量,然后根据参数计算损失的梯度。 接下来,朝着减少损失的方向更新我们的参数。
下面的函数实现小批量随机梯度下降更新。 该函数接受模型参数集合、学习速率和批量大小作为输入。
**每 一步更新的大小由学习速率
lr决定。 因为我们计算的损失是一个批量样本的总和,所以我们用批量大小(
batch_size) 来规范化步长,这样步长大小就不会取决于我们对批量大小的选择。**
def sgd(params, lr, batch_size): #@save
"""小批量随机梯度下降"""
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
1)with torch.no_grad():
更新时不要计算梯度
2)param.grad.zero_()
**pytorch会不断的累加变量的梯度,所以每更新一次参数,就要让其对应的梯度清零 **
3)for param in params:
对每个参数进行计算(可能是w,可能是b)
4)
不除以batch_size损失函数就是平方和误差
我们只要误差就行了
🎄训练
现在我们已经准备好了模型训练所有需要的要素,可以实现主要的训练过程部分了。
理解这段代码至关重要,因为从事深度学习后, 你会一遍又一遍地看到几乎相同的训练过程。
在每次迭代中,我们读取一小批量训练样本,并通过我们的模型来获得一组预测。 计算完损失后,我们开始反向传播,存储每个参数的梯度。
**最后,我们调用优化算法
sgd来更新模型参数。 摘抄来自花书原文**
在每个迭代周期(epoch)中,我们使用
data_iter函数遍历整个数据集, 并将训练数据集中所有样本都使用一次(假设样本数能够被批量大小整除)。 这里的迭代周期个数
num_epochs和学习率
lr都是超参数,分别设为3和0.03。 设置超参数很棘手,需要通过反复试验进行调整。
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X,y in data_iter(batch_size,features,labels):
l = loss(net(X,w,b),y) #X和y的小批量损失
#因为L形状是(batch_size,1)而不是一个标量。L中的所有元素加到一起,
#并因此计算[w,b]梯度
l.sum().backward()
sgd([w,b],lr,batch_size) #使用参数的梯度更新参数
with torch.no_grad():
train_1 = loss(net(features,w,b),labels)
print(f'epoch {epoch+1},loss {float(train_1.mean())}:f')
1)这里用net是指的线性模型,用net因为后面深度学习网络层数相关
如果你没有linreg你会报错
2)l.sum().backward()
求和目的:
之前自动求导那节讲到了向量求梯度比较麻烦 都通过sum()转化为标量再求梯度
求和之后后面会除batch_size,可以计算均值
求和本身让l以标量的形式表现出来。所有的梯度也叠加了嘛,所以sgd里面除了batch_size
它会返回每个epoch的损失 ,看到loss在减少

** 打印一下w 和 b 的误差**
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

版权归原作者 heart_6662 所有, 如有侵权,请联系我们删除。