[CTF/randcrack]python随机数预测模块分析及改进方案

目的

Python中内置了一个random库，用来产生随机数

其内置的算法为梅森算法（Mersenne Twister）

梅森算法具体内容可见：

https://blog.csdn.net/tianshan2010/article/details/83247000

我们今天要关心的是破解梅森算法，也就是预测随机数

首先简单了解一下什么是梅森算法

梅森旋转算法可以产生高质量的伪随机数，并且效率高效，弥补了传统伪随机数生成器的不足。梅森旋转算法的最长周期取自一个梅森素数: $2^{19937} -1$

由此命名为梅森旋转算法。常见的两种为基于32位的MT19937-32和基于64位的MT19937-64

我们注意到一个梅森素数为 $2^{19937} -1$ ，也就是说只要超过梅森素数，我们即可重新回到生成体系中来

思路

说来也简单，我们已经知道随机数的范围（随机数表）就那么大，我们只需要找到随机数从哪儿来的，只要经过一个循环，必定能找到具体的位置，然后就能预测出来了

举个简单的例子：

已知字符串“12345678956789”，如果我们能够知道"34567895678912"，那我们必定能够知道这个循环是从“2”开始的

思路清晰了，我们要解决的就是2个问题，第一，搞到一个梅森素数大小的随机数，然后交给程序分析，找到起始位置，然后预测即可。

解决

找到循环点

由于Python中使用的梅森算法为MT19937

最为广泛使用Mersenne Twister的一种变体是MT19937，可以产生32位整数序列。具有以下的优点:

有 $2^{19937}-1$ 的非常长的周期。在许多软件包中的短周期—232 随机数产生器在一个长周期中不能保证生成随机数的质量。

在1 ≤ k ≤ 623的维度之间都可以均等分布(参见定义).

除了在统计学意义上的不正确的随机数生成器以外，在所有伪随机数生成器法中是最快的(当时)

我们注意到，其生成的数据在62432后会达到循环（注：62332=19936）

由于每次随机产生了32位的随机数，且623次尚未达到2的19937次方的循环点，我们必须需要624个32位由梅森算法产生的随机数才能找到循环点。也就是如果我们能够找到624个32位随机数即可。

进行预测

我们使用randcrack 的Python库进行预测

安装

pip install randcrack -i https://pypi.tuna.tsinghua.edu.cn/simple

使用randcrack库进行预测

Python官方介绍

https://pypi.org/project/randcrack/

来自官方的用法介绍

How to use

It is important to feed crackers exactly 32-bit integers generated by the generator due to the fact that they will be generated anyway, but dropped if you don't request them. As well, you must feed the cracker exactly after a new seed is presented, or after 624*32 bits are generated, since every 624 32-bit numbers generator shifts it's state and the cracker is designed to be fed from the beginning of some state.

Implemented methods

Cracker has one method for feeding:
submit(n)
. After submitting 624 integers it won't take any more and will be ready to predict new numbers.

Cracker can predict new numbers with following methods, which work exactly the same as their siblings from the
random
module but without
predict_
prefix. These are:
predict_getrandbits
,
predict_randbelow
,
predict_randrange
,
predict_randint
,
predict_choice
and
predict_random
Here's an example usage:

import random, time
from randcrack import RandCrack
random.seed(time.time())
rc = RandCrack()
for i in range(624):
    rc.submit(random.getrandbits(32))
    # Could be filled with random.randint(0,4294967294) or random.randrange(0,4294967294)
    print("Random result: {}\nCracker result: {}".format(random.randrange(0, 4294967295), rc.predict_randrange(0, 4294967295)))

当然你不需要去硬啃，大体上翻译一下，就是我们需要去提交624个32位由random模块产生的随机数，然后就可以使用predict进行预测了（random库中提供了一堆随机数模块，如生成k位随机数的getrandbits(k)，随机生成一个整数的randint()，在0-1上随机的random()和在前开后闭区间生成随机数的randrange(),你只需要在前面加个predict_函数名就能预测对应的函数了）

具体用法见下代码:

import random #导入random库（Python内置了）
from randcrack import RandCrack #下载randcrack库后导入类
#你可以掷随机数种子来确保预测的有效性， 不过random预测的时候默认以当前时间作为随机数种子
rc = RandCrack()#实例化randcrack类
for i in range(624):#循环624次
    rc.submit(random.getrandbits(32))#每次循环提交一个32位random生成的随机数
print(random.getrandbits(64))#利用random库获取一个64位的随机数（你可以修改为任意位数）
print(rc.predict_getrandbits(64))#利用randcrack获取的随机数

预测成功！

结束了？

很好，我们已经清晰的破解了random库

但......结束了吗？

不足

我们已经能够实现：只要提交624个32位随机数就能破解random模块了

让我们的思路放开一点，我们能够破解的关键是超过了梅森素数的范围，使得我们能够预测到下一个随机数，而不是在于我们提交了624个32位数。

仔细一想，我们提交624个32位数的目的是为了超过梅森素数，那么，我提交312个64位数可不可以？

从数学上依旧能超过梅森素数

import random
from randcrack import RandCrack

rc = RandCrack()

for i in range(312):
    rc.submit(random.getrandbits(64))#修改为提交了312个64位数

print(random.getrandbits(64))#利用random库获取一个64位的随机数（你可以修改为任意位数）
print(rc.predict_getrandbits(64))#利用randcrack获取的随机数

居然报错了？

我们注意到他的报错是：

ValueError: Didn't recieve enough bits to predict

没有获取的足够的位数去预测

什么鬼？明明31264也是等价于62432的啊？！

那如果我们给他传递624次不足32位的数呢？

import random
from randcrack import RandCrack

rc = RandCrack()

for i in range(624):
    rc.submit(random.getrandbits(24))#修改为提交了624个24位数

print(random.getrandbits(64))#利用random库获取一个64位的随机数（你可以修改为任意位数）
print(rc.predict_getrandbits(64))#利用randcrack获取的随机数

能执行了但是预测的不对

再试试，如果我们溢出提交了呢？

这次我们提交624个64位

import random
from randcrack import RandCrack

rc = RandCrack()

for i in range(624):
    rc.submit(random.getrandbits(64))#修改为提交了624个64位数

print(random.getrandbits(64))#利用random库获取一个64位的随机数（你可以修改为任意位数）
print(rc.predict_getrandbits(64))#利用randcrack获取的随机数

好么，不报错了但是也无法预测了

也就是说，randcrack只能提交624次，少一次都不行，且必须是32位数，位数多了也不行

这也太局限了吧！

优化思路

能不能优化一下，使得他能够兼容呢？

那我们最常见的思路是：

既然就只认624个32位数

那我就从数学上找到一个途径，使得将a个b位数（ab=62432）转化成624个32位数不就能用了？

幸运的是，这个方法存在

证明

让我们通过黑盒测试来研究一下随机数发生的规律

import random
random.seed(1)#掷随机数种子为1从而确保随机数产生的一致性
print(hex(random.getrandbits(32)))
print(hex(random.getrandbits(32)))
random.seed(1)#重新掷随机数种子
print(hex(random.getrandbits(64)))

在这个样例中我们生成了2次32位的随机数并将其转为16进制用来让我们观察规律

然后又生成了一次64位随机数，同样我们转成了16进制

我们惊喜的发现，在两次32位随机数中我们分别把他们记为第一次生成（1），第二次生成（2）

我们观察64位随机数，我们发现，其高32位就是我们第二次生成的随机数，低32位是第一次生成的随机数！

也就是说，**我们的随机数本质上N bit的是由 $\frac{N}{8}$ **个8bit的数据向高位生长产生的

优化代码

我们的随机数本质上N bit的是由 $\frac{N}{8}$ 个8bit的数据向高位生长产生的

得到这个结论后，我们就可以优化randcrack库了

我们可以将用户提交的数据用一个变量存起来，如果这个数大于32位则分割成k个32位数以及一个不足32位的数字，k个32位数按照原来的数的低位向高位进行提交，不足的数等待后续提交后优先提交（因为这个数处于原来的高位和新提交的数的低位，新提交的数应该在不足32位数的基础上进行生长）

图文解释

自己鼠绘的图，见谅

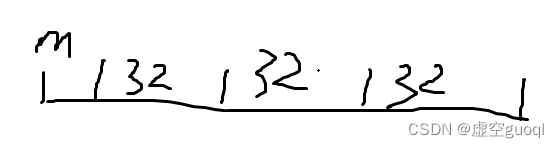
假设一个数有32*3+m位

则提交3次32位数，从右往左依次提交

剩下m位存入缓存区

此时如果再有一个新数32*2+n 位进行提交（如下图）

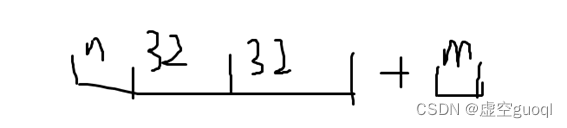
提交后：

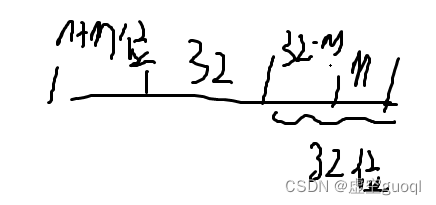
将m优先提交，最后得到m+n位，此时我们再对m+n位数进行判断，如果大于32位则继续提交，小于32位则放于缓存区后继续等待下一次提交

直到提交足够624个32位数后，删除缓存区内的数，同时禁止提交新数用以防止多次提交

参数分析

由于我们32位的数范围在 $0,2^{32}-1$ 内

你无法通过判断有数字长度来确定具体是产生了多少位

因此我们需要两个参数来优化

第一个参数表示提交的数字，第二个参数表示该数字有多少位

同时做好位数校验即可

封装

Easyrandcrack库绝赞编写中~！

大体编程思路（方法不唯一）

import randcrack

class RandCrack(randcrack.RandCrack):
    def __init__(self):
        super().__init__()
    
    def submit(self, num, bits): #num是数据 ，bits 是数据的位数
        #进行优化分解的代码块
        #将数据处理好后调用self._Submit(num)函数即可
        #其实可以用修饰器来的，但是这篇文档本身是写给我们社团的初学者就没弄那么复杂
        #扔到CSDN的时候懒得改了就加了这句话......

    def _Submit(self, num):
        #这里把randcrack自身的submit函数复制过来
        if self.state:
            raise ValueError("Already got enough bits")

        bits = self._to_bitarray(num)

        assert (all([x == 0 or x == 1 for x in bits]))
        self.counter += 1
        self.mt.append(self._harden_inverse(bits))
        if self.counter == 624:
            self._regen()
            self.state = True

例题

GKCTF 2021 Random

BUUCTF做题链接：

https://buuoj.cn/challenges#[GKCTF%202021]Random

wp:

https://blog.csdn.net/m0_62506844/article/details/124278580

ISCTF 2021 RdEs

GitHub题目链接：

https://github.com/ISCTF/ISCTF2021/tree/main/Crypto/RdEs

wp：

NCTF 2022 Coloratura

wp详见NCTF Colorautra详解，这里给出wp（Python代码未经优化）

from Crypto.Util.number import long_to_bytes
from PIL import Image, ImageDraw
from random import getrandbits
from randcrack import RandCrack
from libnum import n2s,s2n
width = 208
height = 208
imgs = Image.open("attach.png")
rc=RandCrack()

def fun(raw:tuple):
        temp = [hex(i)[2:].rjust(2,"0") for i in raw]
        s = temp[2]+temp[1]+temp[0]
        return s

sums=""
count=0
for j in range(4):
        for i in range(width):
                sums= fun(imgs.getpixel((i,j))) + sums
                count+=1

for i in range(623,-1,-1):
        rc.submit(int(sums[8*i:8*i+8],16))

colors_raw = ""
for j in range(height):
        for i in range(width):
                test = rc.predict_getrandbits(32)
                colors_raw = hex(test)[2:].rjust(8,"0") + colors_raw

colors = long_to_bytes(int(colors_raw + sums,16))[::-1]

def makeSourceImg():
        img = Image.new('RGB', (width, height))
        x = 0
        for i in range(height):
            for j in range(width):
                img.putpixel((j, i), (colors[x], colors[x + 1], colors[x + 2]))
                x += 3
        return img
def main():
        raw = makeSourceImg()
        flag = Image.new("RGB", (width, height))
        for i in range(height):
            for j in range(width):
                p1, p2 = imgs.getpixel((j, i)), raw.getpixel((j, i))
                flag.putpixel((j, i), tuple([(p1[k] ^ p2[k]) for k in range(3)]))
        flag.save('flag.png')
 
if __name__ == "__main__":
        main()

标签： python 开发语言网络安全

本文转载自: https://blog.csdn.net/qq_42557115/article/details/128228201
版权归原作者 虚空guoql 所有，如有侵权，请联系我们删除。

[CTF/randcrack]python随机数预测模块分析及改进方案

目的

思路

解决

找到循环点

进行预测

How to use

结束了？

结束了？

不足

优化思路

证明

优化代码

图文解释

参数分析

封装

例题

GKCTF 2021 Random

ISCTF 2021 RdEs

NCTF 2022 Coloratura

发表评论

“[CTF/randcrack]python随机数预测模块分析及改进方案”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航