【关于递归算法的讲解】

递归算法

递归算法是一种通过自身调用自身或间接调用自身来达到问题解决的算法。递归的基本思想是把一个要求解的问题划分成一个或多个规模更小的子问题，这些规模更小的子问题应该与原问题保持同一类型，然后用同样的方法求解规模更小的子问题。

处理重复性计算时，递归往往使函数的定义和算法的描述简单明了，易于理解，容易编程和验证。任何利用计算机求解的问题所需的计算时间与其规模是相关的。问题的规模越小，解题所需的时间也越小，从而容易处理，因此很多复杂问题使用了递推技术能够给出非常直观的解法，结构简介清晰，易于算法分析，在计算机领域，递归算法是不可或缺的。

递归算法的思想

利用递归求解问题的三个特性

• 求解规模为n的问题可以转化为一个或多个结构相同、规模较小的问题，然后从这些小问题的解能方便地构造出大问题的解。
• 递归调用的次数必须是有限的。
• 必须有结束递归的条件（边界条件）来终止递归。

递归算法求解的执行过程

递归算法的执行过程划分为递推和回归两个阶段。在递推阶段，把规模为n的问题的求解推到比原问题的规模较小的问题求解，且必须要有终止递归的条件。在回归阶段，当获得最简单情况的解后，逐级返回，依次得到规模较大问题的解。

例子

求f(n)=2^n.

• 当n=1时，f(1)=2时，f(1)=2可以作为递归出口。
• 当n>1时，f(n)可以分解为f(n)=22^n-1=2f(n-1))。因此原问题f(n)的求解可以转化为求解规模更小的子问题f(n-1)，f(n-1)和***f(n)具有同一问题类型。

•该问题可以用如下递归方程来表示：

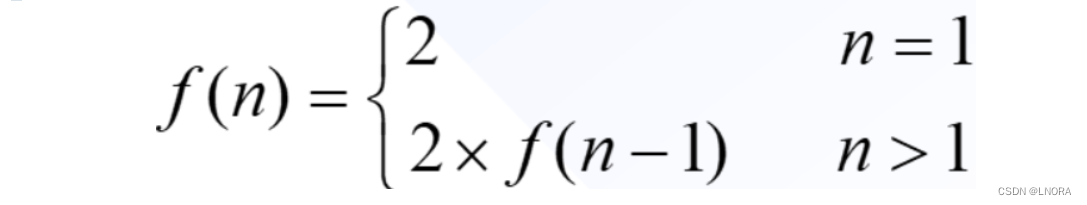
•递归算法的计算过程是由复杂到简单再到复杂 。

递推关系

• 递推关系常用来分析递归算法的时间和空间代价。
• 递推方程是自然数上的一个函数T(n)，它使用一个或多个小于n时的值的等式或不等式来描述。递推方程也称为递推关系或递推式。算法运行时间复杂度主要由关于问题规模的高阶项决定，注意递推方程必须有一个初始条件（也称边界条件）。
• 计算递推式通常有3种方法：替换方法、迭代方法和公式法。

递归算法的应用举例

汉诺塔问题

斐波那契数列问题

八皇后问题

⛵小结

• 递归实质就是实现函数自身调用或者相互调用的过程，递归和归纳关联密切，归纳法是证明递归算法正确性和进行算法分析的强有力工具。
• 递归的运算方法，决定了它的效率较低，一是数据要不断进出栈，另一就是存在大量的重复计算，这样使得应用递归时，输入的n值稍大，程序的求解就变得比较困难，故在有些情况下，递归可以转化为效率较高的非递归。如果这篇【文章】有帮助到你，希望可以点个赞👍，创作不易，如果有对【Java基础】【后端技术】、【数据结构】【Linux操作系统】感兴趣的小可爱，也欢迎关注 【LNORA】，对【算法设计与分析】感兴趣的可以免费订阅【算法设计与分析】的专栏，如果我的文章有帮助到你，麻烦来个一键三连奥，这将是对我莫大的鼓励，我将为大家带来更加优质的文章！我们可以一起进步，每天进步一点点，我将会给你带来巨大的【收获与惊喜】💝💝！