【C语言】探索数据的存储(浮点型篇)

文章目录

1. 前言

上篇文章，我们对整形是如何存储的做出了讲解，而在本篇文章中，我将讲解浮点型是如何存储的，以及对于浮点型数据之间的比较做出一个探究，相信在阅读本篇文章后，你会对数据在内存中的存储有一个新的认识。话不多说，我们进入正题。

2. 浮点型在内存中的存储

浮点数包括float(单精度浮点数）、double(双精度浮点数)、long double类型。

常见的浮点数有：

3.141E10//1.0 * (10 ^ 10)

而浮点数的取值范围的相关信息也在

float.h

中定义。
例如：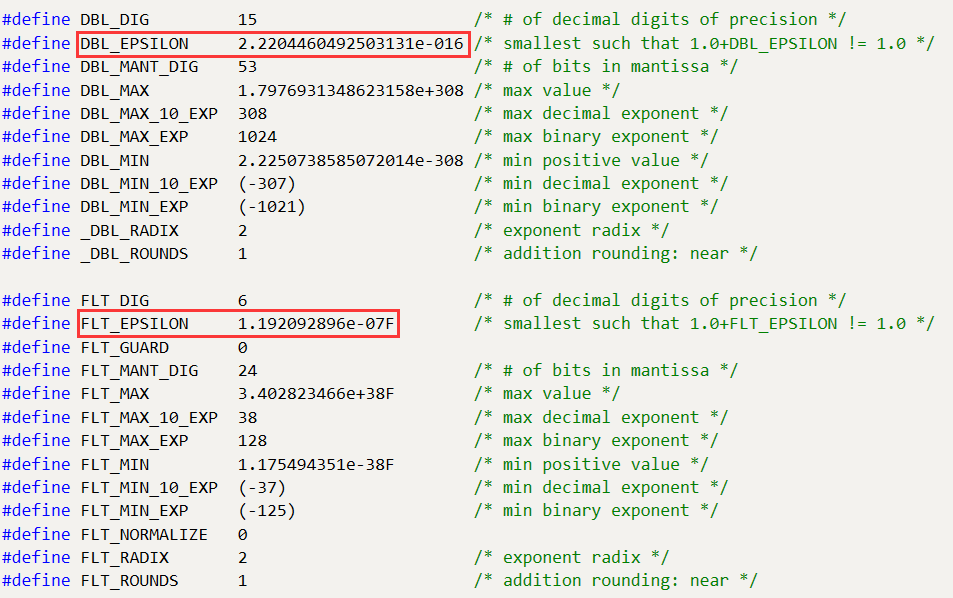

注：DBL_EPSILON和FLT_EPSILON分别是双精度浮点数和单精度浮点数的精度。

了解基本概念之后，我们再看一个关于浮点型存储的经典样例。

3. 例题引入

下列程序输出的结果是什么？

intmain(){int n =9;float* pFloat =(float*)&n;printf("n的值为：%d\n", n);//9printf("*pFloat的值为：%f\n",*pFloat);//0.000000*pFloat =9.0;printf("num的值为：%d\n", n);//1091567616printf("*pFloat的值为：%f\n",*pFloat);//9.000000return0;}

按照我们平常的思路，结果也许为：9，9.0，9，9.0，因为存进去什么样拿出来就应该是什么样，对于浮点型只要加上小数点后六位就好了，但是结果真的是这样吗？让我们运行一下：

发现结果和我们的想法大相庭径，那么说明浮点型和整形在内存中的存储方式是不同的！

接下来让我们了解一下浮点型的存储规则！

4. 浮点数存储规则

根据国际标准IEEE 754，任意一个二进制浮点数可以表示成下面的形式：

• (-1)^S * M * 2^E
• (-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。
• M表示有效数字，大于等于1，小于2。
• 2^E表示指数位。

4.1 浮点数的存

举个栗子：

5.5
    
二进制表示：101.1
解释：(1*2^2+0*2^1+1*2^0).(1*2^(-1))
开始转化：
101.1表示一个整数，所以S =0；
而二进制需要转化成如下形式表示M：101.1->1.011；M >=1&& M <2
由于小数点向左移动两位，所以指数位E为2；

表示结果：(-1)^0*1.011*2^2
               S   M     E

通过如上步骤，5.5就正确按照规则存到了内存中！

我们在观察一下

S E M

在内存中是如何划分的：

32位浮点数：

对于32位浮点数，最高位的1位是符号位S，接着的8位是指数E，剩下的23位为有效数字M。

64位浮点数：

对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。

IEEE 754的特殊规定：

有效数字M：

前面说过， 1≤M<2 ，也就是说，M可以写成1.xxxxxx 的形式，其中xxxxxx表示小数部分。

IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的xxxxxx部分。

比如保存1.01的时候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位浮点数为例，留给M只有23位，

将第一位的1舍去以后，等于可以保存24位有效数字。

指数E：

至于指数E，情况就比较复杂。
首先，E为一个无符号整数，这意味着，如果E为8位，它的取值范围为0255；如果E为11位，它的取值范围为02047。

但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023。

比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

4.2 浮点数的取

了解了浮点数的存储，那么它将数据取出又是什么样的呢？

指数E从内存中取出可以分成三种情况：

E不全为0或不全为1：

这时，浮点数就采用下面的规则表示，即指数E的计算值减去12（或1023），得到真实值，再将有效数字M前加上第一位的1。

比如：

0.5（1/2）的二进制形式为

0.1

，由于规定正数部分必须为1，即将小数点右移1位，则为

1.0*2^(-1)

，在内存中为-1+127=126，表示为01111110，而尾数1.0去掉整数部分为0，补齐0到23位00000000000000000000000，

则其二进制表示形式为:0 01111110 00000000000000000000000

E全为0：

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，

有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。

比如：

0.000000001 * 2 ^(-126)，这是不是一个极小的数字，几乎接近于0(正负取决于符号位s)。

E全为1：

这时，若有效数字M全为0(0/1 11111111 00000000000000000000000)，表示±无穷大。

若有效数字M不全为0，则表示有效数据，是一个非常大的值。

5. 例题解答

intmain(){int n =9;//补码：0000 0000 0000 0000 0000 0000 0000 1001float* pFloat =(float*)&n;//浮点型存储：0 00000000 00000000000000000001001//E为全零，E = 1 - 127 = -126//M不再加上1，M = 0.00000000000000000001001//正数，S = 0//(-1)^0 * 0.00000000000000000001001 * 2^(-126)//几乎为0printf("n的值为：%d\n", n);//存储为整形，取出来也是按照整形的方式取：9printf("*pFloat的值为：%f\n",*pFloat);//0.000000*pFloat =9.0;//二进制表示：1001.0//小数点右移三位：1.001 * 2 ^ 3//S = 0//M = 1.001//E = 3(-1)^0 * 1.001 * 2^3//浮点型存储：0 01000010 00100000000000000000000printf("num的值为：%d\n", n);//1091567616//认为内存中放的是有符号整数，符号位为0，正数//认为二进制序列就是它的原码printf("*pFloat的值为：%f\n",*pFloat);//存储为浮点型，取出来也是按照浮点型的方式取：9.000000return0;}

至此，浮点型的存储方式，你明白了吗？

6. 浮点型的精度探究(※)

此部分为浮点型存储的拓展部分，内容为对浮点型数据之间的比较和浮点型精度的讲解，由于这部分内容在实际学习时很少提及，故归为拓展部分，有兴趣的话可以了解一下。

(由于浮点数默认是double类型，使用float可能会出现告警，考虑到方便起见和double精度更高，所以以下内容均使用double类型)

6.1 浮点数的精度丢失

我们了解了浮点数的存储方式之后，发现浮点数在存储时有时是无法精确保存的，是可能会有精度损失的，注意这里的损失，不是一味的减少了，还有可能增多。浮点数本身存储的时候，在计算不尽的时候，会采用“四舍五入”或者其他策略。

样例：

intmain(){double x =3.6;printf("%.50lf\n", x);return0;}

运行结果：

6.2 浮点数之间如何比较

上述例子意味着，浮点数存入时数据会不一样，这是否说明浮点数之间无法正常比较？事实胜于雄辩，接着探究：

intmain(){double x =1.0;double y =0.1;printf("%.50lf\n", x -0.9);printf("%.50lf\n", y);if((x -0.9)==0.1){printf("==");}else{printf("!=");}return0;}

运行结果：

我们观察结果，发现不仅存储的内容发生了变化，而且直接用

==

相比较得出的结果也是不等于，那么浮点数之间是如何比较的？应该如何理解？

C语言中浮点数应该进行范围精度比较！！！

如图：两个浮点数只要进行比较时，它们的差值，只需要在

-EPS ~ EPS

的精度范围内，那么便认定两个数相等！！！

同样的，条件也可以写成绝对值的形式：

fabs((x - y) < EPSLION)

。fabs是一个库函数，计算变量的绝对值，相关头文件为

#include<math.h>

。

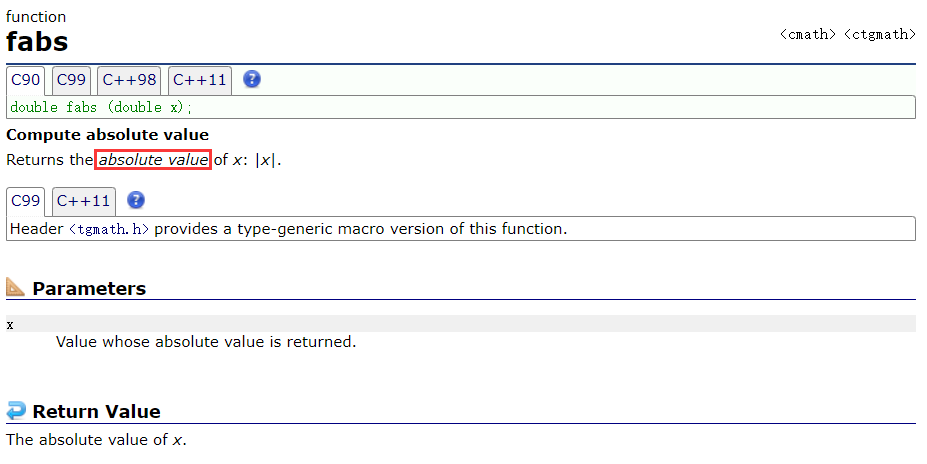
这里的EPSILON是精度，精度分为系统提供的精度(float.h中定义)和自定义的精度：

自定义的精度：

#defineEPS0.00000000000001//自定义的精度，名字，数值可以自定义

系统提供的精度：

#defineDBL_EPSILON//系统提供的精度，需要引头文件#include<float.h>

转到定义观察一下：

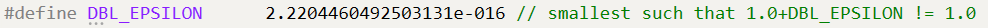
这个数小到什么程度呢？1.0虽然加很多数据都不等于1.0，但是这个

DBL_EPSILON

是最小的。

使用精度后，再进行比较：

//#define EPS 0.00000000000001//自定义方案#defineDBL_EPSILON//系统提供的精度，是一个非常小的值#include<stdio.h>#include<float.h>#include<math.h>intmain(){double x =1.0;double y =0.1;printf("%.50lf\n", x -0.9);printf("%.50lf\n", y);//if (fabs((x - 0.9) - y) < EPS)//自定义if(fabs((x -0.9)- y)< DBL_EPSILON)//系统{printf("==\n");}else{printf("!=\n");}return0;}

运行结果：

6.3 浮点数和0比较

对于两个浮点数之间比较写做

x - y

的形式，那么对于浮点数和0比较就为

x - 0

，直接写做x即可。

样例：

#include<float.h>#include<stdio.h>#include<math.h>intmain(){double x =0.0;if(fabs(x)< DBL_EPSILON)//fabs(x - 0)//if(x > -DBL_EPSILON && x < DBL_EPSILON){printf("yes\n");//一个浮点数和0比较，只要保证它的绝对值在精度范围内就相等}return0;}

运行结果：

但是，浮点数和零值比较要不要相等？

x >= -DBL_EPSILON && x <= DBL_EPSILON)

(

fab(x) <= DBL_EPSILON

)？

精度是引起x变化的最小值，但是精度 + x依旧能引起精度变化；

如果写成fab(x) <= DBL_EPSILON；也就是fab(x) == DBL_EPSILON的形式，这时x就是精度；

double y + x != y;也就是加上x(精度)会引起变化，相当于double y + DBL_EPSILON ！= y;

但是y + 0.0 == y，y加上零值时，值是不会变的！！！

因为精度本身就会引起值的变化，只是很小而已，就不符合0的概念；

写法比较矛盾，不建议写上等号！！！

所以，浮点数和零值进行比较，只要保证浮点数的绝对值在精度范围内，就判定浮点数和零值相等，且比较时，不建议加上等号。

7. 结语

到这里本篇博客到此结束，相信通过这两篇文章，大家也可以对数据在内存中的存储有了一定的认识，虽然这些知识并不会对编程能力有很大的提高，但是能扩大我们看待问题的视角，也算修炼了"内功"。

如果觉得anduin写的还不错的话，还请一键三连！

我是anduin，一名C语言初学者，我们下期见！