数据加密标准DES详细过程总结、代码（自运行可实现）

1、公开征集密码算法标准的主要要求

• 算法必须是安全的：具有加密保护信息安全的能力
• 算法必须是公开的：有完整的算法说明、容易理解、能为所有用户使用
• 能够经济、有效的硬件实现：性能好
• 能够得到批准：合法
• 可出口：大众化

2、DES概述

• 分组加密算法：明文和密文为64位分组长度
• 对称算法：加密和解密除密钥编排不同之外，使用的是同一算法
• 密钥长度：56位，但存在弱密钥，容易避开
• 混乱（S盒）和扩散（P盒）组合，每个组合先代换后置换，共16轮
• 只使用标准的算数和逻辑运算，易于实现。
• 商业密码、现代密码学的标志。

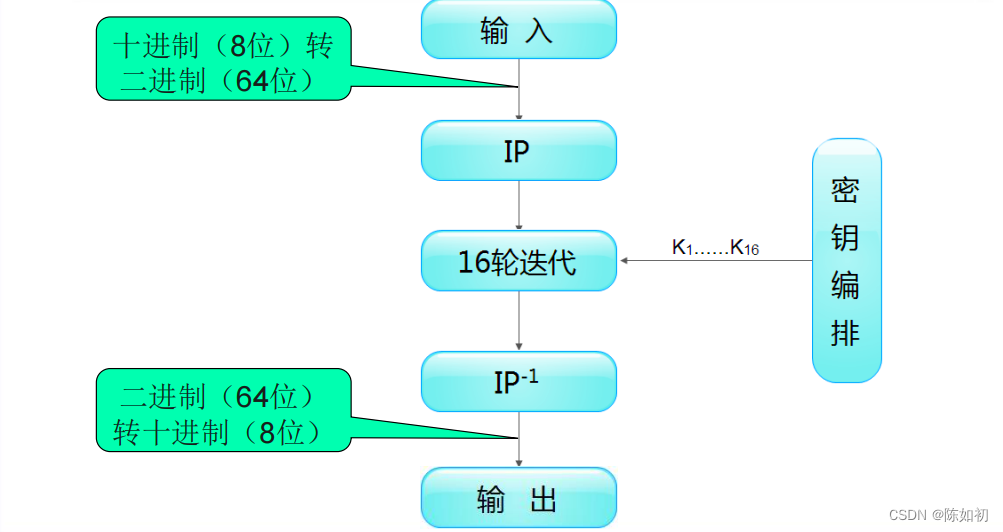
3、DES的实现

（1）、DES算法的整体结构----Feistel结构

*细节流程图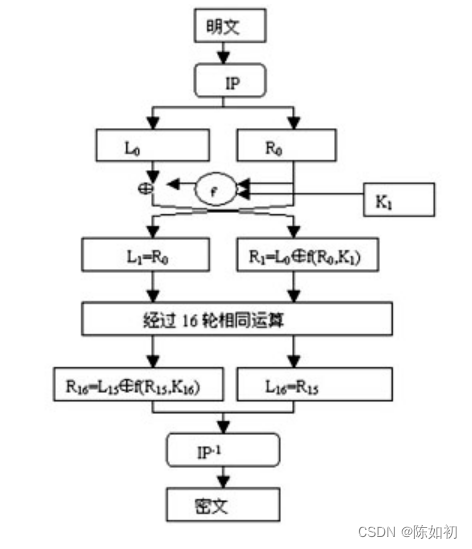

• Feistel提出利用乘积密码可获得简单的代换密码
• Feistel还提出了实现代换和置换的方法
• 很多分组密码的结构从本质上说都是基于一个称 为Feistel网络的结构

（2）、第一步：密钥的编排 （为加密做准备）

1. 密钥生成：

• 从用户处取得一个64位(本文均指二进制位))长的密码口令key ，key=k1k2k3…k63k64。
• 去除64位密码中作为奇偶校验位的第8、16、24、32、40、48、56、64位，剩下的56位作为有效输入密钥。

1. 等分密钥：
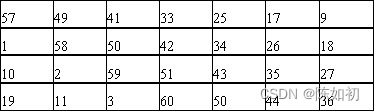
2. 输入密钥位序/ A位序对照表 输入密钥位序/ B位序对照表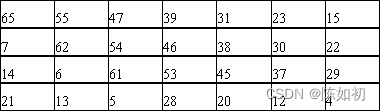 这样 key=k1k2k3…k55k56 形成了A、B两部分： A = k57k49k41…k44k36 B=k65k55k47…k12k4
3. 密钥移位DES算法的密钥是经过16次迭代（循环左移）得到一组密钥的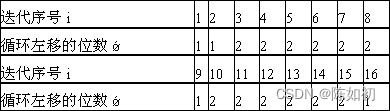Ps：生成的A、B视为迭代的起始密钥，上表显示每一次迭代时密钥循环左移的位数。 比如在第1次迭代时密钥循环左移1位，第3次迭代时密钥循环左移2位…第9次迭代时密钥循环左移1位，第14次迭代时密钥循环左移2位。
4. 迭代并乘积合并得到密钥C

• 第一次迭代： A(1) =(1) A
• 第i次迭代： A(i) =(i) A(i-1) B(i) =(i) B(i-1)
• 第i次迭代生成的两个28位长的密钥并乘积得到56位密钥C(i)=A（i）B(i)=A(i)1…A(i)28B(i)1…B(i)28

1. 对密钥C进行加密，故产生加密密钥K

• 56位密钥C的位序与加密密钥K的位序对照表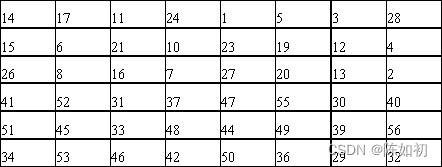Ps：k的第一位为56位密钥的第14位，k的第2位为56位密钥的第17位，依此类推，k的最后一位第48位是56位密钥的第32位。 这样，就生成了一个48位使用密钥：K=k(i)1k(i)2…k(i)48

1. DES算法密钥生成需要进行16次迭代，在完成16次迭代前，循环执行上述第4步和第5步，最终形成16套加密密钥：key[0]，key[1]，key[2]，…。key[14]，key[15]。即以下第二步

（3）、第二步：16轮迭代

按下述规则进行16次迭代：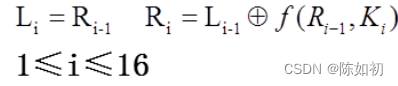
Ps1：这里的 “＋” 是对应比特的模加2，f 是一个函数（轮函数）。
Ps2：16个长度为48比特的子密钥ki(1≤i≤16)是由密钥k经密钥编排函数计算出来的。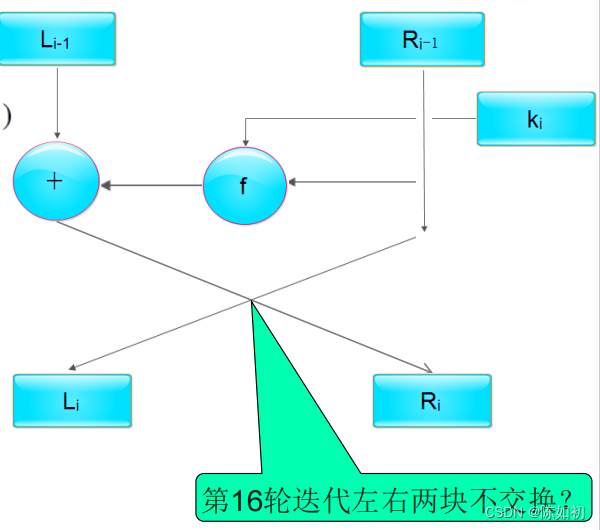
Ps3：第16轮迭代左右数值不做交换

（4）、第三步：IP置换（加密）

给定明文，通过一个固定的初始置换IP来重排输入明文块P中的比特，得到比特串P0=IP（P）=L0R0，这 里L0和R0分别是P0的前32比特和后32比特
Ps：利用乘积密码可获得简单的代换密码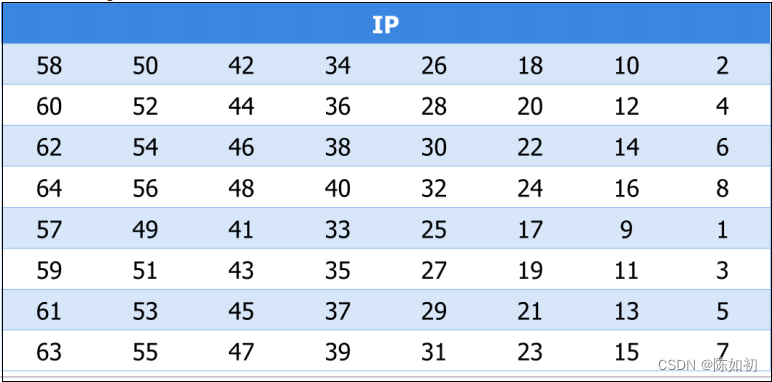

（5）、第四步：IP逆置（解密）

对比特串R16L16使用逆置换IP-1得到密文C，即
C=IP-1 (R16L16)。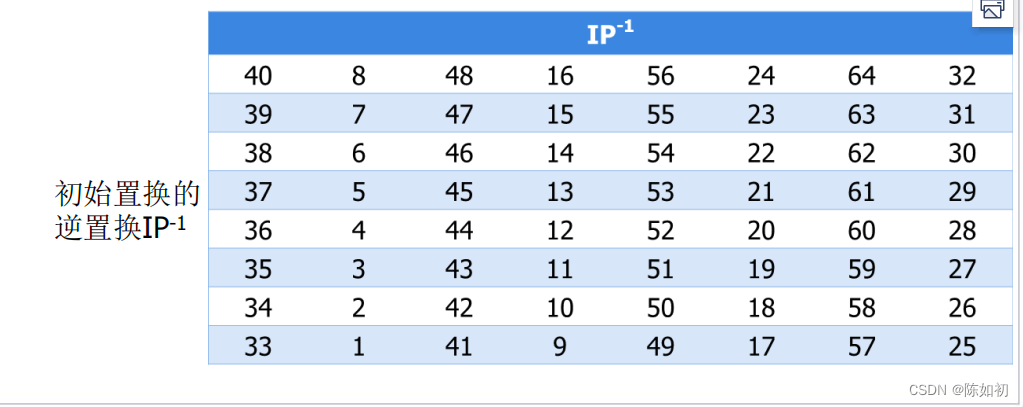

***以上为含图简介，为了更好理解这个过程，避免看很多头疼的流程图，我们用文字叙述的方式来简述加密解密的详细过程，即以上（4）、（5）为数据加密解密的简介，以下为具体过程：

1.总体过程
DES对64位明文分组进行操作。通过一个初始置换，将明文分组分成左半部分和右半部分，各32位长。
然后进行16轮完全相同的运算，这些运算被称为函数 f，在运算过程中数据与密钥结合。经过16轮
后，左、右半部分合在一起经过一个末置换（初始置换的逆置换），算法就完成了。
在每一轮中，密钥位移位，然后再从密钥的56位中选出48位。通过一个扩展置换将数据的右半部分
扩展成48位，并通过一个异或操作与48位密钥结合，通过 8个S盒将这48位替代成新的32位数据，再
将其置换一次。这四步运算构成了函数f。然后，通过另一个异或运算，函数f的输出与左半部分结合，
其结果即成 为新的左半部分。将该操作重复16次，便实现了DES的16轮运算。
假设Bi是第i次迭代的结果，Li和Ri是Bi的左半部分和右半部分，Ki是第i轮的48位密钥，且f是实现
代替、置换及密钥异或等运算的函数，那么每一轮就是：
 Li=Ri-1
 Ri=Li-1⊕f(Ri-1,Ki)

2、初始置换
初始置换在第一轮运算之前进行，对输入分组实施如下表所示的变换。初始置换把明文的第58位换到第1位的位置，把第50位换到第2位的位置，把第42位换到第3位的位置，以此类推。
58, 50, 42, 34, 26, 18, 10, 2, 60, 52, 44, 36, 28, 20, 12, 4
62, 54, 46, 38, 30, 22, 14, 6, 64, 56, 48, 40, 32, 24, 16, 8
57, 49, 41, 33, 25, 17, 9, 1, 59, 51, 43, 35, 27, 19, 11, 3
61, 53, 45, 37, 29, 21, 13, 5, 63, 55, 47, 39, 31, 23, 15, 7
初始置换和对应的末置换并不影响DES的安全性，它们的主要目的是为了更容易地将明文和密文数据以字节大小放入DES芯片中。

3、密钥置换
由于不考虑每个字节的第8位，DES的密钥由64位减至56位，每个字节第8位作为奇偶校验以确保密钥不发生错误。如下表所示：
57, 49, 41, 33, 25, 17, 9, 1, 58, 50, 42, 34, 26, 18
10, 2, 59, 51, 43, 35, 27, 19, 11, 3, 60, 52, 44, 36
63, 55, 47, 39, 31, 23, 15, 7, 62, 54, 46, 38, 30, 22
14, 6, 61, 53, 45, 37, 29, 21, 13, 5, 28, 20, 12, 4
在DES的每一轮中，从56位密钥产生出不同的48位子密钥(subkey)，这些子密钥是这样确定的：
首先，56位密钥被分成两部分，每部分28位。
然后，根据轮数，这两部分分别循环左移1位或2位。每轮移动的位数如下表：
轮 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
位数 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
移动后，就从56位中选出48位。这个运算既置换了每位的顺序，也选择了子密钥，被称为压缩置换(compression permutation)。下表即定义了压缩置换：
14, 17, 11, 24, 1, 5, 3, 28, 15, 6, 21, 10
23, 19, 12, 4, 26, 8, 16, 7, 27, 20, 13, 2
41, 52, 31, 37, 47, 55, 30, 40, 51, 45, 33, 48
44, 49, 39, 56, 34, 53, 46, 42, 50, 36, 29, 32
可以看出，第33位的那一位在输出时移到了第35位，而处于第18位的那一位被忽略了。

4、扩展置换****（轮函数f的一部分）
这个运算将数据的右半部分从32位扩展到48位。这个操作两方面的目的：它产生了与密钥同长度的数据以进行异或运算；它提供了更长的结果，使得在替代运算中能进行压缩。
对每个4位输入分组，第1位和第4位分别表示输出分组中的两位，而第2位和第3位分别表示输出分组中的一位，下表给出了哪一输出位对应哪一输入位：
32, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9
8, 9, 10, 11, 12, 13, 12, 13, 14, 15, 16, 17
16, 17, 18, 19, 20, 21, 20, 21, 22, 23, 24, 25
24, 25, 26, 27, 28, 29, 28, 29, 30, 31, 32, 1
处于输入分组中第3位的位置移到了输出分组中的第4位，而输入分组的第21位则移到了输出分组的第30位和第32位。尽管输出分组大于输入分组，但每一个输入分组产生唯一的输出分组。

5、S盒代替****（轮函数f的一部分）
压 缩后的密钥与扩展分组异或以后，将48位的结果送入，进行代替运算。替代由8个S盒完成，每一个S盒都由6位输入，4位输出，且这8个S盒是不同的。48 位的输入被分为8个6位的分组，每一个分组对应一个S盒代替操作：分组1由S盒1操作，分组2由S盒2操作，等等。如下图所示：
每一个S盒是一个4行、16列的表。盒中的每一项都是一个4位的数。S盒的6个位输入确定了其对应的输出在哪一行哪一列。下表列出所有8个S盒：
S盒1:
14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13
S盒2:
15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9
S盒3:
10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12
S盒4:
7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5 ,11, 12, 4, 15
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14
S盒5:
2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3
S盒6:
12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13
S盒7:
4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12
S盒8:
13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11
假定将S盒的6位的输入标记位b1、b2、b3、b4、b5、b6。则b1和b6组合构成了一个2位数，从0到3，它对应着表的一行。从b2到b5构成了一个4位数，从0到15，对应着表中的一列。
例如，假设第6个S盒的输入为110011，第1位和第6位组合形成了11，对应着第6个S盒的第三行，中间4位组合形成了1001，它对应着同一个S盒的第9列，S盒6在第三行第9列的数是14，则用值1110来代替110011。
这是DES算法的关键步骤，所有其他的运算都是线性的，易于分析，而S盒是非线性的，它比DES的其他任何一步提供了更好的安全性。
这个代替过程的结果是8个4位的分组，他们重新合在一起形成了一个32位的分组。

6、P盒置换****（轮函数f的一部分）
S盒代替运算的32位输出依照P盒进行置换。该置换把每输入位映射到输出位，任一位不能被映射两次，也不能被略去，下表给出了每位移至的位置：
16, 7, 20, 21, 29, 12, 28, 17, 1, 15, 23, 26, 5, 18, 31, 10
2, 8, 24, 14, 32, 27, 3, 9, 19, 13, 30, 6, 22, 11, 4, 25
第21位移到了第4位，同时第4位移到了第31位。
最后，将P盒置换的结果与最初的64位分组的左半部分异或，然后左、右半部分交换，接着开始另一轮。

7、末置换****（轮函数f的一部分）
末置换是初始置换的逆过程。DES在最后一轮后，左半部分和右半部分并未交换，而是将两部分并在一起形成一个分组作为末置换的输入，该置换如下表如示：
40, 8, 48, 16, 56, 24, 64, 32, 39, 7, 47, 15, 55, 23, 63, 31
38, 6, 46, 14, 54, 22, 62, 30, 37, 5, 45, 13, 53, 21, 61, 29
36, 4, 44, 12, 52, 20, 60, 28, 35, 3, 43, 11, 51, 19, 59, 27
34, 2, 42, 10, 50, 18, 58, 26, 33, 1, 41, 9, 49, 17, 57, 25

8、DES的解密
DES使得用相同的函数来加密或解密每个分组成为可能，二者唯一的不同就是密钥的次序相反。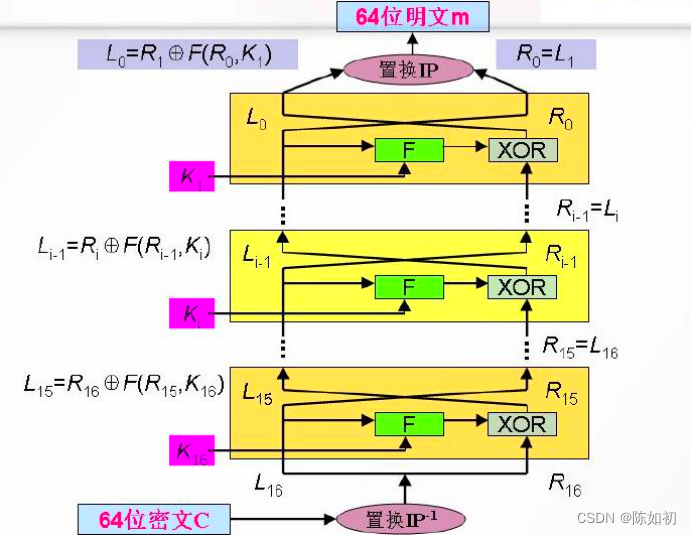

4、S盒设计的重要性

& DES的核心是S盒，除此之外的计算是线性的
& S盒作为该密码体制的非线性组件对安全性至
关重要
& S盒的设计准则：
1、 具有良好的非线性（输出的每一个比特与全部
输入比特有关）
2、每一行包括所有16种4位二进制
3、两个输入相差1bit时，输出相差2bit
4、 如果两个输入刚好在中间两个比特上不同，则
输出至少有两个比特不同
5、 如果两个输入前两位不同而最后两位相同，则
输出一定不同
6、 相差6bit的输入共有32对，在这32对中有不超
过8对的输出相同

5、DES缺陷

 密钥分配问题：通信双方要进行加密通信，
需要通过秘密的安全信道协商加密密钥，而
这种安全信道可能很难实现

 密钥管理问题：在有多个用户的网络中，任
何两个用户之间都需要有共享的秘密钥，当
网络中的用户n很大时，需要管理的密钥数目
非常大n(n-1)/2

 互补性，是由算法中的两次异或运算的配置所决定的。两次异或运算一次在S盒之前，一次在P盒置换之后。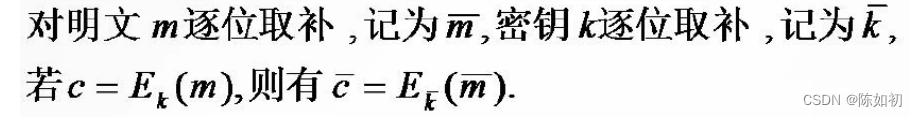

若对DES输入的明文和密钥同时取补，则选择扩展运算E的输出和子密钥产生器的输出也都取补，因
而经异或运算后的输出和明文及密钥未取补时的输出一样，这使得到达S盒的输入数据未变，其输出自然也不会变，但经第二个异或运算时，由于左边的数据已取补，因而输出也就取补了

互补性会使DES在选择明文攻击下所需的工作量减半

 弱密钥和半弱密钥

1、弱密钥

• 如果给定初始密钥k，经子密钥产生器产生的各个子密钥都相同，即有kl=k2=…=k16，则称给定的初始密钥k为弱密钥。
• 若 k 为 弱 密 钥 ， 则 对 任 意 的 64bit 信 息 有 ：Ek(Ek(m))=m和Dk(Dk(m))=m
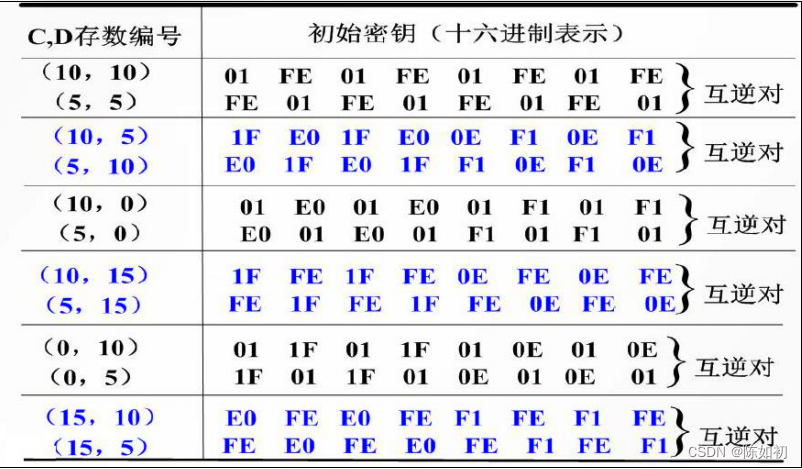
• 弱密钥的构造由子密钥产生器中寄存器C和D中的存 数在循环移位下出现重复图样决定的（C和D中的存 数为全0或全1）共有4个（十六进制）：

2、半弱密钥

• 若给定初始密钥k，产生的16个子密钥只有两种，且每种都出现8次，则称k为半弱密钥。
• 半弱密钥的特点是成对出现， 且具有下述性质： 若k1和k2为一对弱密钥，m为明文组，则有：Ek2(Ek1(m))=Ek1(Ek2(m))=m此外，还有四分之一弱密钥等。
• DES的密钥中，弱密钥的比例非常小，而且极易避开，因此，弱密钥的存在对DES的安全性威胁不大。

 密钥搜索

DES的强度：56比特的密钥长度：

• 如果每秒搜索106个密钥，大约需要100年。
• 采用并行技术，97年10万美金的机器(5760个搜索5xl07芯片) 1.5天用穷举法找到DES密钥。
• 密钥分割的方法：利用Internet的分布式计算能力， 组织志愿者连接了100000台计算机系统，在22小时15分钟完成DES算法的攻击。

 差分分析和线性分析

• 差分分析是一种攻击迭代密码体制的选择明文攻击 方法
• 与一般统计分析法的不同之处是，它不是直接分析密文或密钥和明文的统计相关性，而是分析一对给定明文的异或（称为差分）与对应密文对的 异或之间的统计相关性。
• 差分分析的基本思想是在要攻击的迭代密码系统中找出某些高概率的明文差分和密文差分对来推算密钥。 利用此法攻击DES，需要用247个选择明文和247次加密运算，比穷举搜索的工作量大大减少。

 线性分析（实际上不可行）

• 基本思想是：以最佳的线性函数逼近DES的非线 性变换S盒，这是一种已知明文攻击方法，可以在 有243个已知明文的情况下破译DES。
• 虽然获得已知明文比选择明文更容易，但线性分析作为一种攻击 手段在实际上仍然不可行

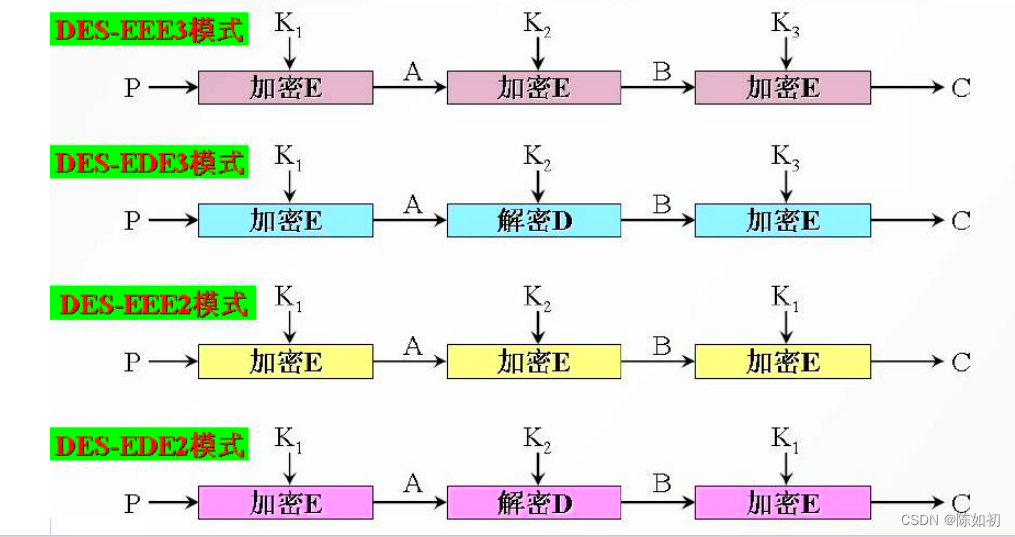
6、多重DES

1. 为了提高DES的安全性能，并充分利用有关DES的现有软件和硬件资源，可以使用多重DES。
2. 多重DES就是使用多个密钥利用DES对明文进行多次加密。
3. 使用多重DES可以增加密钥量，从而大大提高抵抗密钥的穷举搜索攻击的能力。
4. 已经证明多重DES并不等价于多次使用一个56位密钥的单重DES。
5. 二重DES/三重DES
6. 多重DES的四种模式：

7、代码

#include<stdio.h>#include<stdlib.h>#include<string.h>#include<openssl/des.h>#pragmacomment(lib,"libssl.lib")#pragmacomment(lib,"libcrypto.lib")
using namespace std;/************************************************************************
** 本例采用：
** 3des-ecb加密方式；
** 24位密钥，不足24位的右补0x00；
** 加密内容8位补齐，补齐方式为：少1位补一个0x01,少2位补两个0x02,...
** 本身已8位对齐的，后面补八个0x08。
************************************************************************/intmain(void){int docontinue =1;char data[20]="hello world!";/* 明文 */int data_len;int data_rest;unsignedchar ch;unsignedchar* src =NULL;/* 补齐后的明文 */unsignedchar* dst =NULL;/* 解密后的明文 */int len;unsignedchar tmp[8];unsignedchar in[8];unsignedchar out[8];char k[100]="01234567899876543210";/* 原始密钥 */int key_len;#defineLEN_OF_KEY24unsignedchar key[LEN_OF_KEY];/* 补齐后的密钥 */unsignedchar block_key[9];
    DES_key_schedule ks, ks2, ks3;/* 构造补齐后的密钥 */
    key_len =strlen(k);memcpy(key, k, key_len);memset(key + key_len,0x00, LEN_OF_KEY - key_len);/* 分析补齐明文所需空间及补齐填充数据 */
    data_len =strlen(data);
    data_rest = data_len %8;
    len = data_len +(8- data_rest);
    ch =8- data_rest;
    src =(unsignedchar*)malloc(len);
    dst =(unsignedchar*)malloc(len);if(NULL== src ||NULL== dst){
        docontinue =0;}if(docontinue){int count;int i;/* 构造补齐后的加密内容 */memset(src,0, len);memcpy(src, data, data_len);memset(src + data_len, ch,8- data_rest);/* 密钥置换 */memset(block_key,0,sizeof(block_key));memcpy(block_key, key +0,8);DES_set_key_unchecked((const_DES_cblock*)block_key,&ks);memcpy(block_key, key +8,8);DES_set_key_unchecked((const_DES_cblock*)block_key,&ks2);memcpy(block_key, key +16,8);DES_set_key_unchecked((const_DES_cblock*)block_key,&ks3);printf("before encrypt:\n");for(i =0; i < len; i++){printf("0x%.2X ",*(src + i));}printf("\n");/* 循环加密/解密，每8字节一次 */
        count = len /8;for(i =0; i < count; i++){memset(tmp,0,8);memset(in,0,8);memset(out,0,8);memcpy(tmp, src +8* i,8);/* 加密 */DES_ecb3_encrypt((const_DES_cblock*)tmp,(DES_cblock*)in,&ks,&ks2,&ks3, DES_ENCRYPT);/* 解密 */DES_ecb3_encrypt((const_DES_cblock*)in,(DES_cblock*)out,&ks,&ks2,&ks3, DES_DECRYPT);/* 将解密的内容拷贝到解密后的明文 */memcpy(dst +8* i, out,8);}printf("after decrypt :\n");for(i =0; i < len; i++){printf("0x%.2X ",*(dst + i));}printf("\n");}if(NULL!= src){free(src);
        src =NULL;}if(NULL!= dst){free(dst);
        dst =NULL;}return0;}