大整数乘法的详解

一.问题

由于编程语言提供的基本数值数据类型表示的数值范围有限，不能满足较大规模的高精度数值计算，因此需要利用其他方法实现高精度数值的计算，于是产生了大数运算。尤其是乘法运算，下面就是大整数的乘法的过程（加 减法都一样的原理）。

二.解决问题的方法

方法一（传统的相乘逐步相加）

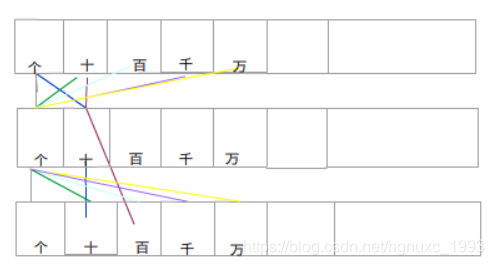
乘法规律，一个数的第i位和另一个数的第j位相乘，一定会累加到结果的第i+j位，结果的数组一个数组元素存2位数，最后对结果整除得到进位，mod得到余数就是i+j位的数字，最后打印出来。

** 对于大整数比较方便的输入方法*是，①按字符型处理，存储在字符串数组s1、s2中，计算结果存储在整型数组ans中。 ②通过字符的ASCII码，数字字符可以直接参与运算，i位数字与j位数字相乘的表达式为：(s1[i]-‘0’)(s2[j]-‘0’)。 ③每一次数字相乘的结果位数是不固定的，而结果数组中每个元素只存储一位数字，所以用变量t暂存结果，对t mod运算得到的就是ans[i+j]的值，若超过1位数则进位，用变量b存储。

这种做法的时间复杂度为o(n^2)

c语言源码：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
int max(int a,int b){
    return a>b?a:b;
}
 
int main()
 {
  char s1[205], s2[205],ans[1000];
  int str1[205],str2[205]；
  int len1, len2,i;
  while( scanf("%s%s", s1, s2)!=EOF){
     len1 = strlen(s1), len2 = strlen(s2);
     memset(str1,0,205);//初始化0
     memset(str2,0,205);
     memset(ans,0,1000);
     int len = 0;
     for(i = 0; i < len1; ++ i)
        str1[i] = s1[len1 - 1 - i] - '0';
     for(i = 0; i < len2; ++ i)
         str2[i] = s2[len2 - 1 - i] - '0';
 
    for( i = 0; i < len1; ++ i)
    {
         int b = 0;   //每遍历完数组a的一个数，进位b都要初始化为0
         for(int j = 0; j < len2 || b; ++ j)//当str[j]没遍历完，或者最高位满十需要进位，进位不为0
         {
             int t = ans[i + j] + str1[i]*str2[j] + b;
             ans[i + j] = t%10;  //余数就是该ans[i+j]位置的数
             b = t/10;//进位
             //len = max(len, j + i);
         }
        len = i+j-1  //最终的位数
     }
     for( i = len; i >= 0; -- i)  //倒置输出
        printf("%d", ans[i]);
     printf("\n");
  }
    return 0;
}

方法二（分治法）

分治算法解题的一般步骤：

• 分解：将要解决的问题划分为若干个规模较小的同类问题
• 求解：当子问题划分的足够小时，用较简单的方法解决
• 合并：按原问题的要求，将子问题的解逐层合并构成原问题的解

①两个大整数在理想状态下：就是两个大整数的位数相同

现在有两个大整数X,Y; 设X, Y是n位十进制整数，分段表示如下:

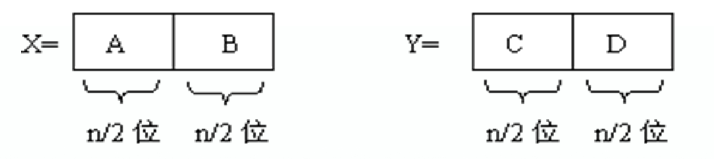
即 X=A10^(n/2)+B, Y=C10^(n/2)+D 则:

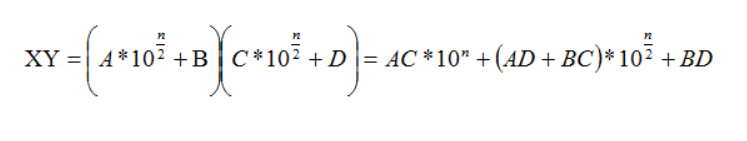
本来可以直接算AD+BC，但是这样效率变低了，所以对AD+BC进行分解优化后得：

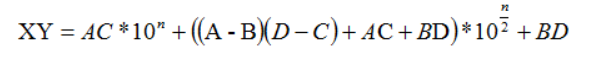
计算成本：3次n/2位乘法，6次不超过n位加减法，2次移位，所有加法和移位共计O(n)次运算。由此可得

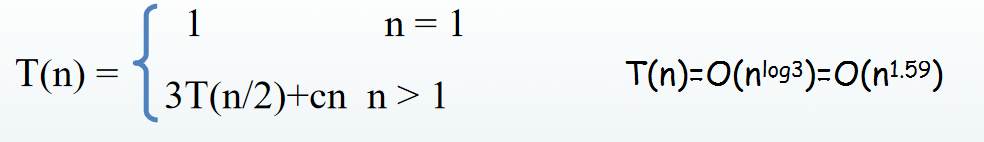
理想状态下c语言代码：（不超过long long 型，后面做法会用字符串接收大整数）

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#define sign(x) ((x>0)?1:-1)

//_int64等同于long long 
//%I64d等同于%lld

 _int64 mutipy(_int64 a,_int64 b,int num){  //两个long long 类型的大整数相乘，后面会用字符串做法解决
     int s=sign(a)*sign(b);
     a=(a>0)?a:-a ;
     b=(b>0)?b:-b ;
     if(num==0)  //递归出口，
         return 0;
     else if(num==1){  //当a,b只有一位数时，直接相乘
         return s*a*b;  
     }
     else{

       _int64 A=a/(int)pow(10,(int)(num/2));  //分离大整数a的高位
       _int64 B=a%(int)pow(10,(int)(num/2)); //分离大整数a的低位
       _int64 C=b/(int)pow(10,(int)(num/2));   //分离大整数b的高位
       _int64 D=b%(int)pow(10,(int)(num/2));     //分离大整数b的低位

       _int64 AC=mutipy(A,C,(int)(num/2));  //分治计算AC
       _int64 BD=mutipy(B,D,(int)(num/2));  //分治计算BD
       _int64 ABCD=mutipy((A-B),(D-C),(int)(num/2))+AC+BD;  //计算(A-B)(D-C)+AC+BD
       return s*(_int64)(AC*pow(10,(int)(num/2)+(int)(num/2))+ABCD*pow(10,(int)(num/2))+BD);  //返回结果
     }
} 
int main()
 {
    _int64 a,b,c,temp;  //long long a,b,c;
    int len1=0,len2=0;

    while(scanf("%I64d %I64d",&a,&b)){
        temp=a;
        while(temp){  //计算a的位数
            len1++;
             temp=temp/10;
        }    
       c=mutipy(a,b,len1);
       printf("%I64d\n",c);    
    }
    return 0;
}

其实上述有个缺陷：那就是只能是long long 类型的大整数相乘，超出了long long 型就会报错。解决方法看下面的做法

②两个大整数在非理想状态下：就是两个大整数的位数不相同

我们还是假设有两个大整数X、Y，它们的位数不相同，现在要求X*Y的乘法，我们采用分治的算法，将X、Y分别拆分为A与B、C与D，如下图:

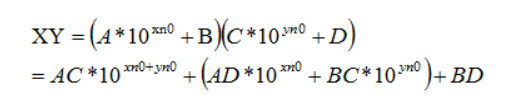
上式一共需要进行2次xn0的乘法（AC、AD各一次）、2次yn0的乘法（AC、BC各一次）和3次加法，因而该算法的时间复杂度为

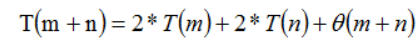
跟上面一样，对AD+BC进行分解优化得：

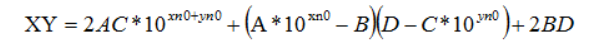
修改后的时间复杂度：

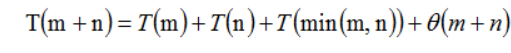
由于T(min(m,n))<T(m)+T(n),所以修改后的算法更好，时间复杂度：T(m+n)=O(nlog3)=O(n1.59)

非理想状态下的c语言代码：（不超过long long 型，后面做法会用字符串接收大整数）

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#define sign(x) ((x>0)?1:-1)
//_int64等同于long long 
//%I64d等同于%lld

 _int64 mutipy(_int64 a,int numa,_int64 b,int numb){ //两个long long 类型的大整数相乘，后面会用字符串做法解决
     int s=sign(a)*sign(b);
     a=(a>0)?a:-a ;
     b=(b>0)?b:-b ;
     if(numa==0||numb==0)  //递归出口，
         return 0;
     else if((numa==1&&numb==1)||numa==1||numb==1){  //当a,b只有一位数时，直接相乘
         return s*a*b;  
     }
     else{
       int num1=numa/2;  //定义了大整数a的低位的位数x0
       int num2=numa-num1;  //定义了大整数a的高位的位数x1
       int num3=numb/2;   //定义了大整数b的低位的位数x2
       int num4=numb-num3; //定义了大整数b的高位的位数x3

       _int64 A=a/(int)pow(10,num1);  //分离大整数a的高位
       _int64 B=a%(int)pow(10,num1); //分离大整数a的低位
       _int64 C=b/(int)pow(10,num3);   //分离大整数b的高位
       _int64 D=b%(int)pow(10,num3);     //分离大整数b的低位

       _int64 AC=mutipy(A,num2,C,num4);  //分治计算AC
       _int64 BD=mutipy(B,num1,D,num3);  //分治计算BD
       _int64 ABCD=mutipy(((_int64)(A*pow(10,num1))-B),num2,(D-(_int64)(C*pow(10,num1))),num4);  //计算(A*10^num1-B)(D-C*10^num3)
       return s*(_int64)(2*AC*pow(10,(num1+num3))+ABCD+2*BD);  //返回结果     
     }
}
int main()
 {
    _int64 a,b,c,temp;  //long long a,b,c;
    int len1=0,len2=0;

    while(scanf("%I64d %I64d",&a,&b)){
        temp=a;
        while(temp){  //计算a的位数
            len1++;
             temp=temp/10;
        }
        temp=b;
        while(temp){      //计算b的位数
            len2++;
             temp=temp/10;
        }    
       c=mutipy(a,len1,b,len2);
       printf("%I64d\n",c);    
    }  
    return 0;
}

非理想状态下的c语言代码：（任意位数相乘，可以超出longlong类型）

#include<stdio.h>
#include<string.h>
int result[255];

 void cal( char a[],int numa,char b[],int numb,int s){
   int num1=numa/2;     //num1为B的位数，B属于低位的那一部分
   int num2=numa-num1;  //num2为A的位数，A属于高位的那一部分
   int num3=numb/2;    //num3为D的位数，D属于低位的那一部分
   int num4=numb-num3;  //num4为C的位数，C属于高位的那一部分
   char A[255],B[255],C[255],D[255];
   int k=0;
   if(numa==0||numb==0)  //当位数为0时
        return ;
   else if(numa==1&&numb==1){  //分治递归到当数组a和b的位数全为1时
         result[s]+=(a[0]-'0')*(b[0]-'0');  //直接计算，把他的结果直接加到对应数组result的位置
         return;
         }
   else{  //当数组a和b的位数至少有一个不为1时
       
       for(int i=0;i<num2;i++) //获取数组a的高位部分A
           A[k++]=a[i];
       k=0;
       for(i=num2;i<numa;i++)  //获取数组a的低位部分B
           B[k++]=a[i];
       k=0;
       for(i=0;i<num4;i++)  //获取数组b的高位部分C
           C[k++]=b[i];
       k=0;
       for(i=num4;i<numb;i++)  //获取数组b的高位部分D
           D[k++]=b[i];

       cal(A,num2,C,num4,s+num1+num3);  //AC ,在result[s+num1+num3]的位置存储AC，也是说偏移s+num1+num3位，s初始化为0
       cal(B,num1,C,num4,num3+s);  //BC，偏移num3+s位
       cal(A,num2,D,num3,num1+s);  //AD,偏移num1+s位
       cal(B,num1,D,num3,s);  //BD，偏移s位
   }
 }
 void exchange(int result[],int len){ //将result数组中的值进行整理，转化输出
    int i = 0;
    int t,p1,p2;
    while(i<=len){    //以特殊数最大位数为终止条件 
        if(result[i] < 10);      //当result[i]的值小于10，就不处理，直接保存在result[i]中
        else if(result[i] < 100){  //当0<=result[i]<100时
            t = result[i] % 10;  //余数就是该位置result[i]的值
            p1 = result[i] / 10;  //result[i]进位
            result[i] = t;       //将余数t保存至result[i]中
            result[i+1] += p1;   //进位把他加到result[i+1]中    
        }
        else{   //当result[i]>=100时
            t = result[i] % 10;     //余数就是该位置result[i]的值
            p1 = result[i] / 10 % 10;  //这是result[i]满十进位
            p2 = result[i] / 100;       //这是result[i+1]满十进位 
            result[i] = t;         //将余数t保存至result[i]中
            result[i+1] += p1;     //进位把他加到result[i+1]中
            result[i+2] += p2;     //进位把他加到result[i+2]中
        }
        i++;  //位数加1
    } 
}

 int main(){
   char a[100],b[100];
   int j,i=0,len1,len2;
  while(scanf("%s %s",a,b)!=EOF){
   len1=strlen(a);
   len2=strlen(b);
   cal(a,len1,b,len2,0);  
   exchange(result,len1+len2); 

   for(i=len1+len2-1;i>=0;){  //去高位的0去掉
       if(result[i]==0){  
         while(result[i]==0){
           i--;
         }
       }
       else
           break;
   }

   for(j=i;j>=0;j--) //从非零的位置打印
         printf("%d",result[j]);         
   printf("\n");
  }
   return 0;
 }