0
0

用C语言写一个计算器

用C语言写一个计算器，除了四则混合运算之外，还支持三角函数和绝对值等函数。

PS E:\Code\PL\calc>.\a.exe     
abs(3*5-4^2)abs(3*5-4^2)=1.00000025-7+6*(4-5)25-7+6*(4-5)=12.000000

文章目录

在计算器中，至少包含两类变量，即数字和运算符。例如，如果希望实现

    a
   
   
    +
   
   
    b
   
   
    ×
   
   
    (
   
   
    c
   
   
    −
   
   
    d
   
   
    )
   
  
  
   a+b\times (c-d)
  
 
a+b×(c−d)这样一个简单的功能，要求编译器可以识别出

 
  
   
    +
   
   
    ,
   
   
    ×
   
   
    ,
   
   
    −
   
   
    ,
   
   
    (
   
   
    ,
   
   
    )
   
  
  
   +,\times,-,(,)
  
 
+,×,−,(,)这五个符号，并理清彼此的计算顺序，最后生成一棵语法树，然后实现输出。

1. 加减法运算

万事开头难，所以我们选择一个简单到无脑的开头。首先，我们考虑实现

    a
   
   
    +
   
   
    b
   
  
  
   a+b
  
 
a+b这样简单的两数运算，即如下所示，十分简单且无脑。

voiddouCalc(){while(1){double i, j, s;char k;scanf("%lf%c%lf",&i,&k,&j);switch(k){case'+':
            s = i+j;break;case'-':
            s = i-j;break;case'*':
            s = i*j;break;case'/':
            s = i/j;break;default:break;}printf("%lf\n", s);}}

然后，我们考虑，如何实现一个连加器，旨在解决

    a
   
   
    +
   
   
    b
   
   
    +
   
   
    c
   
   
    +
   
   
    .
   
   
    .
   
   
    .
   
  
  
   a+b+c+...
  
 
a+b+c+...的计算问题。这里虽然不涉及到运算次序，但仍旧需要处理多个不确定个数的变量，所以我们不再可以直接用类似

scanf("%lf%c%lf", &i, &k, &j);

的方案来实现数据的输入，而必须建立一个链表来存储变量。

C语言输入输出

在C语言中，可以通过至少三种方式来读取键盘输入的值：

  • scanf()：和 printf() 类似，scanf() 可以输入多种类型的数据。
  • getchar()、getche()、getch()：这三个函数都用于输入单个字符。
  • gets()：获取一行数据，并作为字符串处理。

其中，

scanf

是格式化扫描的意思，可以通过格式控制符对输入字符进行格式化，并赋值给相关变量。
格式控制符说明%c读取单一字符%s读取一个字符串（以空白符为结束）%f、%lf读取十进制形式小数，赋值给float、double 类型%e、%le读取指数形式小数，赋值给 float、double 类型%g、%lg读取十进制或指数形式的小数，
并分别赋值给 float、double 类型

  • 整数格式化 shortintlong十进制%hd%d%ld八进制%ho%o%lo十六进制%hx%x%lx无符号%hu%u%lu
getchar()

等价于

scanf("%c", c)

，相对来说更加简单。

getche

和

getch

是Windows独有的函数，在头文件

conio.h

中故不赘述。

gets

和

scanf(%s,s)

的区别在于，后者在使用的过程中会把空格当作终止符，而前者不会。

所以，我们在实现连加的过程中，会使用

gets

作为交互方法。

由于我们实现的是一个连加器，所以输入字符中只包含数字和加号，那么接下来，我们需要遍历输入字符，通过加号来将数字分开。我们可以很方便地写下一个简单而丑陋的小程序。

voidadds(){char str[100];char numStr[20];int num[20];int val;int i,j,k;while(1){gets(str);
        i =0;j =0;k =0;while(str[i]!='\0'){if(str[i]=='+'){
                num[k]=atoi(numStr);
                k++;
                j =0;}else{
                numStr[j]= str[i];
                j++;}
            i++;}
        num[k]=atoi(numStr);
        val =0;for(int i =0; i < k+1; i++){
            val += num[i];}printf("%d\n",val);}}intmain(){adds();return0;}

由于加减法具有相同的运算优先级，在实现上不过是为后续的数字加上一个负号而已，故可十分方便地在原有程序上修改。

此外，

adds

代码乍看上去没什么问题，但

str

的值在更新之前，并不会自动清零，由此带来的bug需要创建一个字符串清零的函数。修改之后的代码如下

#include<stdio.h>#include<stdio.h>#include<string.h>#include<math.h>voidstrClear(char*str,int n){for(int i =0; i < n; i++){
        str[i]=NULL;}}voidadds(){char str[100];char numStr[20];int num[20];int val;int i,j,k;while(1){gets(str);
        i =0;j =0;k =0;while(str[i]!='\0'){if(str[i]=='+'){
                num[k]=atoi(numStr);strClear(numStr,20);
                k++;
                j =0;}elseif(str[i]=='-'){
                num[k]=atoi(numStr);strClear(numStr,20);
                k++;
                numStr[0]= str[i];
                j =1;}else{
                numStr[j]= str[i];
                j++;}
            i++;}
        num[k]=atoi(numStr);strClear(numStr,20);
        val =0;for(int i =0; i < k+1; i++){
            val += num[i];}printf("%d\n",val);}}intmain(){adds();return0;}

精简一下

#include<stdio.h>#include<stdio.h>#include<string.h>#include<math.h>voidstrClear(char*str,int n){for(int i =0; i < n; i++){
        str[i]='\0';}}voidadds1(){char str[100];char numStr[20];int i,j,val;while(1){gets(str);
        i =0;j =0;val =0;while(str[i]!='\0'){if((str[i]=='+')||(str[i]=='-')){
                val +=atoi(numStr);strClear(numStr,20);
                j =0;if(str[i]=='-')
                    numStr[j++]=str[i];}else
                numStr[j++]= str[i];
            i++;}
        val +=atoi(numStr);strClear(numStr,20);printf("%d\n",val);}}intmain(){adds1();return0;}

2. 加法和乘法

若希望加入乘法和除法，那么修改代码的过程就相对复杂了，因为乘除法在运算过程中，具有比加减法更高的优先级。那么我们就无法通过一个简单的数组来存储变量，而必须建立一种树形的结构。

例如，对于

    a
   
   
    +
   
   
    b
   
   
    ×
   
   
    c
   
   
    −
   
   
    d
   
   
    ×
   
   
    e
   
   
    /
   
   
    f
   
  
  
   a+b\times c-d\times e/f
  
 
a+b×c−d×e/f，可写成如下形式

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ruufs0c0-1608717185925)(img/calc1.png)]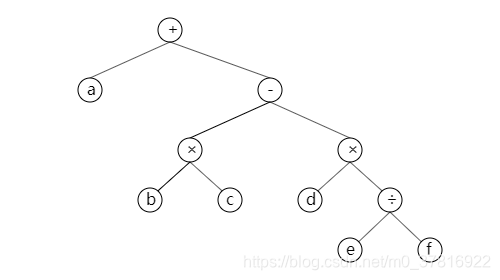
在这里插入图片描述

我们可以看到，这是一个二叉树，每个叶节点都是数字，而两个叶节点的父节点则为运算符。我们通过这个运算符来计算其子节点后，删除它的两个子节点，同时运算符所对应的节点退化为叶节点，同时其类型也变为数字。

对于上图而言，先计算

    e
   
   
    /
   
   
    f
   
  
  
   e/f
  
 
e/f，然后计算

 
  
   
    b
   
   
    ×
   
   
    c
   
  
  
   b\times c
  
 
b×c和

 
  
   
    d
   
   
    ×
   
   
    e
   
   
    /
   
   
    f
   
  
  
   d\times e/f
  
 
d×e/f，再计算

 
  
   
    b
   
   
    ×
   
   
    c
   
   
    −
   
   
    d
   
   
    ×
   
   
    e
   
   
    /
   
   
    f
   
  
  
   b\times c-d\times e/f
  
 
b×c−d×e/f，最后计算最上面的加法。

对于树来说，我们的遍历往往从根节点开始，所以其计算规则如下：

  1. 如果当前节点的子节点为叶节点，则计算当前节点，并删除该节点的叶节点，然后考虑其父节点。
  2. 如果当前节点的某个子节点不是叶节点，则处理该子节点，直到该子节点成为叶节点为止。
  3. 如果当前节点为根节点，且为叶节点，则输出计算结果。

对于节点来说，除了父子节点外，则至少有两个属性：

  1. isLeaf：用于叶节点判定。在这里，叶节点不仅有结构上的意义，更有着明确的语义：它只能是数字。
  2. value：对于叶节点而言，这个值为数字，否则的话，这个值为运算符号及其所对应的计算规则。
#defineMAXLEN100typedefstructNODE{structNODE*father;structNODE*Left;structNODE*Right;char value[MAXLEN];int isLeaf;}Node;

生成计算树

由于我们规定了两个运算层级，所以再遍历字符串以生成计算树的过程中，需要两次循环，即首先生成加减法的计算树，然后再生成乘除法的计算树。

生成计算树的过程可以简化为字符串不断拆分的过程，为了简化思维，我们只考虑两个符号

+

和

*

，这两个符号分别代表两种计算层级。

由此可得到如下代码。对于

#defineTRUE1#defineFALSE0voidnewNode(Node *root, Node *father){
    root -> father = father;
    root ->Left =NULL;
    root -> Right =NULL;
    root -> isLeaf = FALSE;}//root 为根节点，str为字符串voidinitCalcTree(Node *root,char flag){for(int i =0; i < MAXLEN; i++){if(root->value[i]==flag){
            Node *Left =(Node *)malloc(sizeof(Node));
            Node *Right =(Node *)malloc(sizeof(Node));newNode(Left,root);newNode(Right,root);for(int j =0; j < i; j++)
                Left -> value[j]= root->value[j];
            Left->value[i]='\0';
            i++;for(int j = i; j < MAXLEN; j++)
                Right -> value[j-i]= root->value[j];

            root->Left = Left;
            root->Right = Right;strClear(root->value,MAXLEN);
            root->value[0]= flag;
            root->value[1]='\n';initCalcTree(Left,'*');if(flag=='+')initCalcTree(Right,'+');elseinitCalcTree(Right,'*');break;}else{if(root->value[i]=='\0'){if(flag =='+')initCalcTree(root,'*');else
                    root -> isLeaf = TRUE;break;}elsecontinue;}}}

测试一下

voidprintNode(Node *root,int start){printf("the %dth node is %s\n", start, root->value);if(root->isLeaf==FALSE){printNode(root->Left, start +1);printNode(root->Right, start +1);}}intmain(){
    Node *root =(Node *)malloc(sizeof(Node));char*str ="1+21*3+3*4*5+6";strcpy(root->value,str);initCalcTree(root,'+');printNode(root,0);return0;}

得到结果为

the 0th node is +

the 1th node is 1
the 1th node is +

the 2th node is *

the 3th node is 21
the 3th node is 3
the 2th node is +

the 3th node is *

the 4th node is 3
the 4th node is *

the 5th node is 4
the 5th node is 5
the 3th node is 6

然后，我们再对计算树进行计算。当被计算的量为叶节点时，则返回该节点的值；如果该节点的两个节点都是叶节点，则返回该节点处的运算符对这两个子节点的计算值；如果该节点的两个节点都不是叶节点，那么对这两个子节点进行计算。

intcalcNode(Node *root){if(root->isLeaf == TRUE)returnatoi(root->value);elseif(root->Left->isLeaf * root->Right->isLeaf == TRUE){if(root->value[0]=='+')returnatoi(root->Left->value)+atoi(root->Right->value);elseatoi(root->Left->value)*atoi(root->Right->value);}else{if(root->value[0]=='+')returncalcNode(root->Left)+calcNode(root->Right);elsereturncalcNode(root->Left)*calcNode(root->Right);}}intmain(){
    Node *root =(Node *)malloc(sizeof(Node));char str[MAXLEN];while(1){gets(str);strcpy(root->value,str);initCalcTree(root,'+');printf("%s=%d\n",str,calcNode(root));}return0;}

结果为

PS E:\Code\PL\calc>.\a.exe
1+2+3*4+15*21+2+3*4+15*2=452*5+3*6*122*5+3*6*12=226

3. 四则混合运算

如果考虑加减乘除，那么意味着一个运算级别下有多种运算符，所以我们需要通过一个函数来返回运算符的运算次序。

intgetOrder(char ch){int result;switch(ch){case'+':case'-':return0;case'*':case'/':return1;default:return2;}}

然后，基于此，修改计算树的生成与计算代码。

intdouCalc(char c,int a,int b){switch(c){case'+':return a+b;case'-':return a-b;case'*':return a*b;case'/':return a/b;}}voidnewNode(Node *root, Node *father){
    root -> father = father;
    root ->Left =NULL;
    root -> Right =NULL;
    root -> isLeaf = TRUE;
    father -> isLeaf = FALSE;}//root 为根节点，str为字符串，N为字符串长度voidinitCalcTree(Node *root,int order){for(int i =0; i < MAXLEN; i++){if(getOrder(root->value[i])==order){
            Node *Left =(Node *)malloc(sizeof(Node));
            Node *Right =(Node *)malloc(sizeof(Node));newNode(Left,root);newNode(Right,root);for(int j =0; j < i; j++)
                Left -> value[j]= root->value[j];
            Left->value[i]='\0';
            i++;for(int j = i; j < MAXLEN; j++)
                Right -> value[j-i]= root->value[j];

            root->Left = Left;
            root->Right = Right;

            root->value[0]= root->value[i-1];
            root->value[1]='\0';initCalcTree(Right,order);if(order<1)initCalcTree(Left,order+1);break;}elseif((i==0)&&(order<2))initCalcTree(root,order+1);}}intcalcNode(Node *root){if(root->isLeaf == TRUE)returnatoi(root->value);elseif(root->Left->isLeaf * root->Right->isLeaf == TRUE)returndouCalc(root->value[0],atoi(root->Left->value),atoi(root->Right->value));elsereturndouCalc(root->value[0],calcNode(root->Left),calcNode(root->Right));}intmain(){
    Node *root =(Node *)malloc(sizeof(Node));char str[MAXLEN];while(1){gets(str);strcpy(root->value,str);initCalcTree(root,0);printf("%s=%d\n",str,calcNode(root));}return0;}

至此，我们得到了一个计算器的“骨架”，为运算符设定相应的运算次序，相当于提供一种生成方法，这种方法可以直接扩展到更多的运算符上。

同时，上述代码中也出现了两个问题：

  1. 我们默认计算的是整型数据，所以无法处理浮点型运算
  2. 减法和除法虽然在名义上与加法、乘法处于相同的运算次序中，但我们的生成树中默认的是从右向左计算。对于 a + b − c + d a+b-c+d a+b−c+d这样的表达式，会计算成 a + b − ( c + d ) a+b-(c+d) a+b−(c+d)的形式，这是错误的。

针对这种运算结构的一个优势和两个问题，我们继续改进这个计算器程序。

4. 浮点型计算器程序

首先，我们将所有函数与变量均改为

double

类型；然后我们更改输入字符串的遍历方式，从后向前进行遍历。

我们再加入乘方运算符

^

，给它一个更高的运算层级

intgetOrder(char ch){int result;switch(ch){case'+':case'-':return0;case'*':case'/':return1;case'^':return2;case'0':case'1':case'2':case'3':case'4':case'5':case'6':case'7':case'8':case'9':return3;default:return4;}}doubledouCalc(char c,double a,double b){switch(c){case'+':return a+b;case'-':return a-b;case'*':return a*b;case'/':return a/b;case'^':returnpow(a,b);}}

至此，我们写出了一个可以计算

+-x÷^

的程序。但我们还不能处理表达式中可能出现的括号。

括号在表达式中成对出现，故不同于常规运算符，需要在表达式的两端进行遍历；另外，括号不具备运算功能，只有规定运算次序的作用，对于括号运算符只有一个子节点。所以，只需更改

initCalcTree

的代码。

由于我们将算法改为从右向左遍历，所以如果最后一个字符不是

)

，则不必考虑括号的影响。当最后一个字符为

)

时，如果第0个字符为

(

，则将括号里面的内容提取出来，针对此时的节点重新进行遍历即可。如果自左向右遍历的过程出现第一个

(

的位置是

posLeft

，则后面关于运算符的遍历从

posLeft

开始。

//root 为根节点，str为字符串，N为字符串长度voidinitCalcTree(Node *root,int order){int lenStr =strlen(root->value);int posLeft = lenStr;//如果末尾为')'，则查找其对应的左括号的位置if(root->value[lenStr-1]==')'){for(int i =0; i < lenStr; i++)if(root->value[i]=='(')
                    posLeft = i;if(posLeft ==0){for(int i =1; i < lenStr-1; i++)
                root->value[i-1]= root->value[i];
            root->value[lenStr-2]='\0';initCalcTree(root,0);}}//如果左括号的位置不为0，则for(int i = posLeft; i >=0; i--){if(getOrder(root->value[i])==order){
            Node *Left =(Node *)malloc(sizeof(Node));
            Node *Right =(Node *)malloc(sizeof(Node));newNode(Left,root);newNode(Right,root);for(int j =0; j < i; j++)
                Left -> value[j]= root->value[j];
            Left->value[i]='\0';
            i++;for(int j = i; j < MAXLEN; j++)
                Right -> value[j-i]= root->value[j];

            root->Left = Left;
            root->Right = Right;

            root->value[0]= root->value[i-1];
            root->value[1]='\0';//字符串末尾标记initCalcTree(Left,order);if((order<2)||(posLeft!=lenStr))initCalcTree(Right,order+1);break;}elseif((i==0)&&(order<2))initCalcTree(root,order+1);}}

至此，我们就写好了一个简陋的可以进行四则混合运算的计算器程序

PS E:\Code\PL\calc>.\a.exe     
1+2*(3-4)+51+2*(3-4)+5=4.0000002^(3+1)2^(3+1)=16.000000

5. 加入三角函数

现在我们需要考虑加入三角函数，其难点在于函数的识别。

我们规定，单变量函数通过括号的方式导入实参，也就是说，只要表达式中不出现括号，那么就不必考虑括号的问题。换句话说，判定函数，必然在判定括号之后。

考虑到我们定义的

getOrder

函数中，除了我们所规定的符号和数字之外，其他符号和字母的默认返回值为4。所以需要在判定括号之后，继续进行函数的判断。

故而需要更改括号判定的代码

/*...*/if(root->value[lenStr-1]==')'){for(int i =0; i < lenStr; i++)if(root->value[i]=='(')
                     posLeft = i;if(posLeft ==0){for(int i =1; i < lenStr-1; i++)
                root->value[i-1]= root->value[i];
            root->value[lenStr-2]='\0';initCalcTree(root,0);}else{int lenFunc=0;
            posLeft--;while((getOrder(root->value[posLeft])==4)&&(posLeft>0)){
                posLeft--;
                lenFunc++;}//当posLeft变为0时，说明此节点为无法分割的函数if(posLeft==0){
                root->value[lenFunc+1]='\0';
                Node *Left =(Node *)malloc(sizeof(Node));
                root->Left = Left;newNode(Left,root);for(int i = lenFunc+2; i < lenStr-1; i++){
                    Left->value[i-lenFunc-2]=root->value[i];}
                Left->value[lenStr-lenFunc-2]='\0';initCalcTree(Left,0);//对左子节点进行生成return0;}}}/*...*/

接下来，我们需要修改

calcNode

函数，即在计算运算符之前，添加一个函数处理程序。其中，

strcmp

为字符串比对函数，当两个字符串相等时，返回0。

doubledoFunc(char*str,double val){if(strcmp(str,"sin")==0)returnsin(val);elseif(strcmp(str,"cos")==0)returncos(val);elseif(strcmp(str,"tan")==0)returntan(val);elseif(strcmp(str,"arcsin")==0)returnasin(val);elseif(strcmp(str,"arccos")==0)returnacos(val);elseif(strcmp(str,"arctan")==0)returnatan(val);elseif(strcmp(str,"sqrt")==0)returnsqrt(val);elseif(strcmp(str,"abs")==0)returnabs(val);}doublecalcNode(Node *root){if(getOrder(root->value[0])==4)returndoFunc(root->value,calcNode(root->Left));if(root->isLeaf == TRUE)returnatof(root->value);elseif(root->Left->isLeaf * root->Right->isLeaf == TRUE)returndouCalc(root->value[0],atof(root->Left->value),atof(root->Right->value));elsereturndouCalc(root->value[0],calcNode(root->Left),calcNode(root->Right));}

至此，我们已经用C语言实现了一个简陋而且有不少bug的计算器，比如并未设置除零报警之类的功能，但一般的操作是没有问题的。

abs(3*5-4^2)abs(3*5-4^2)=1.00000025-7+6*(4-5)25-7+6*(4-5)=12.000000
标签： C语言 计算器 编译原理
本文转载自: https://blog.csdn.net/m0_37816922/article/details/111595416
版权归原作者 微小冷 所有， 如有侵权，请联系我们删除。
登录后发布评论

“用C语言写一个计算器”的评论:

还没有评论
关于作者
...
overfit同步小助手
文章同步
相关阅读

docker 安装 mysql

使用idea和vecode创建vue项目并启动（超详细）

科普文：微服务之SpringBoot性能优化器动态线程池【Dynamic-Tp】特性和源码解读

[实时计算flink]双流JOIN语句

【若依】若依Vue3前端拆解分析--布局分析--index篇

Spring Boot 3.4.0 发行：革新与突破的里程碑

索引（MySQL）

文章导航