大家好,我是微学AI,今天给大家介绍一下人工智能(pytorch)搭建模型10-pytorch搭建脉冲神经网络(SNN)实现及应用,脉冲神经网络(SNN)是一种基于生物神经系统的神经网络模型,它通过模拟神经元之间的电信号传递来实现信息处理。与传统的人工神经网络(ANN)不同,SNN 中的神经元能够生成脉冲信号,并且这些信号在神经网络中以时序的方式传播。
目录
- 引言
- 脉冲神经网络(SNN)简介
- SNN原理
- 使用PyTorch搭建SNN模型
- 数据样例与加载
- 训练SNN模型
- 测试SNN模型
- 总结
1. 引言
脉冲神经网络(SNN)是一种模拟生物神经元行为的神经网络模型,具有较高的计算效率和能量效率。本文将介绍SNN的基本原理,并使用PyTorch框架搭建一个简单的SNN模型。我们将使用一些数据样例进行训练和测试,展示SNN模型的性能。
2. 脉冲神经网络(SNN)简介
脉冲神经网络(SNN)是一种受生物神经系统启发的神经网络模型,其神经元之间通过脉冲进行通信。与传统的人工神经网络(ANN)相比,SNN具有更高的计算效率和能量效率,因此在某些应用场景中具有较大的潜力。
3. SNN原理
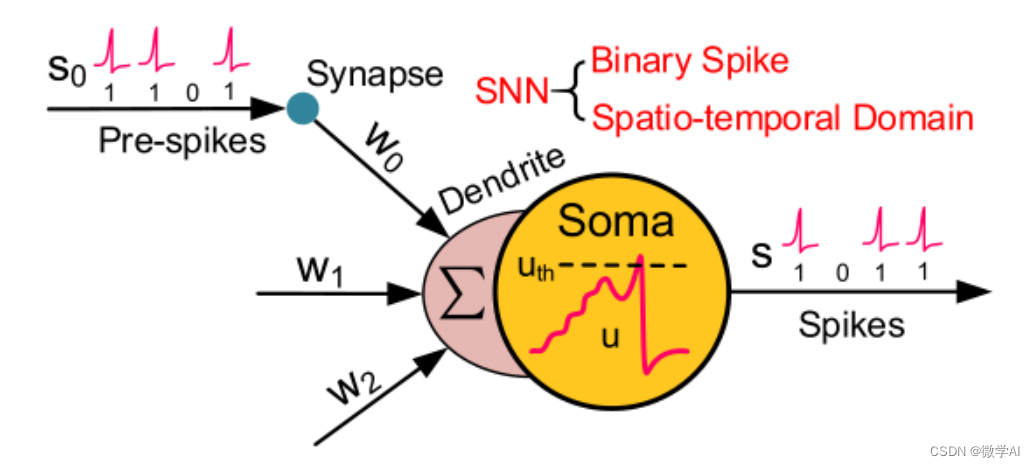
SNN的基本原理是模拟生物神经元的工作机制。在SNN中,神经元通过脉冲(spike)进行通信。当神经元的膜电位(membrane potential)达到阈值时,神经元就会发放一个脉冲,并将膜电位重置为初始值。脉冲通过突触(synapse)传递给其他神经元,从而实现神经元之间的通信。
SNN的一个关键特性是其动态性。神经元的状态随时间变化,这使得SNN能够处理时序数据。此外,SNN具有稀疏性,即神经元只在需要时发放脉冲,这有助于降低计算和能量消耗。
SNN数学原理可以用以下公式表示:
u
i
(
t
)
=
∑
j
=
1
N
w
i
j
x
j
(
t
)
u_i(t)=\sum_{j=1}^N w_{ij}x_j(t)
ui(t)=j=1∑Nwijxj(t)
τ
i
d
u
i
(
t
)
d
t
=
−
u
i
(
t
)
+
∑
j
=
1
N
w
i
j
x
j
(
t
)
\tau_i\frac{du_i(t)}{dt}=-u_i(t)+\sum_{j=1}^N w_{ij}x_j(t)
τidtdui(t)=−ui(t)+j=1∑Nwijxj(t)
其中,
u
i
(
t
)
u_i(t)
ui(t)表示神经元
i
i
i在时间
t
t
t的膜电,
x
j
(
t
)
x_j(t)
xj(t)表示神经元
j
j
j在时间
t
t
t的输入脉冲,
w
i
j
w_{ij}
wij表示神经元
i
i
i和
j
j
j之间的连接权重,
τ
i
\tau_i
τi表示神经元
i
i
i的时间常数。
当神经元的膜电位
u
i
(
t
)
u_i(t)
ui(t)超过了一个阈值
θ
i
\theta_i
θi时,神经元会发放一个脉冲输出。因此,SNN的输出可以表示为:
y
i
(
t
)
=
∑
j
=
1
N
w
i
j
s
j
(
t
)
y_i(t)=\sum_{j=1}^N w_{ij}s_j(t)
yi(t)=j=1∑Nwijsj(t)
其中,
s
j
(
t
)
s_j(t)
sj(t)表示神经元
j
j
j在时间
t
t
t的脉冲输出。
这些公式描述了SNN的基本数学原理,其中包括神经元的输入、膜电位和输出。
4. 使用PyTorch搭建SNN模型
在本节中,我们将使用PyTorch框架搭建一个简单的SNN模型。首先,我们需要导入所需的库:
import torch
import torch.nn as nn
import torch.optim as optim
接下来,我们定义一个脉冲神经元(spiking neuron)类,该类继承自
nn.Module
:
classSpikingNeuron(nn.Module):def__init__(self, threshold=1.0, decay=0.9):super(SpikingNeuron, self).__init__()
self.threshold = threshold
self.decay = decay
self.membrane_potential =0defforward(self, x):
self.membrane_potential += x
spike =(self.membrane_potential >= self.threshold).float()
self.membrane_potential = self.membrane_potential *(1- spike)* self.decay
return spike
然后,我们定义一个简单的SNN模型,包含一个输入层、一个隐藏层和一个输出层:
classSNN(nn.Module):def__init__(self, input_size, hidden_size, output_size):super(SNN, self).__init__()
self.input_layer = nn.Linear(input_size, hidden_size)
self.hidden_layer = SpikingNeuron()
self.output_layer = nn.Linear(hidden_size, output_size)defforward(self, x):
x = self.input_layer(x)
x = self.hidden_layer(x)
x = self.output_layer(x)return x
5. 数据样例与加载
为了训练和测试我们的SNN模型,我们需要一些数据样例。在这里,我们使用一个简单的二分类问题,数据集包含两类线性可分的点。我们可以使用
torch.utils.data.TensorDataset
和
torch.utils.data.DataLoader
来加载数据:
import torch.utils.data as data
# 生成数据样例
X = torch.randn(1000,2)
y =(X[:,0]+ X[:,1]>0).float()# 创建数据加载器
dataset = data.TensorDataset(X, y)
data_loader = data.DataLoader(dataset, batch_size=10, shuffle=True)
6. 训练SNN模型
接下来,我们将训练我们的SNN模型。首先,我们需要实例化模型、损失函数和优化器:
model = SNN(input_size=2, hidden_size=10, output_size=1)
criterion = nn.BCEWithLogitsLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)
然后,我们进行多个epoch的训练,并在每个epoch后打印损失值和准确率:
num_epochs =200for epoch inrange(num_epochs):
epoch_loss =0
correct =0
total =0for X_batch, y_batch in data_loader:
optimizer.zero_grad()
outputs = model(X_batch)
loss = criterion(outputs.view(-1), y_batch)
loss.backward()
optimizer.step()
epoch_loss += loss.item()
correct +=((outputs.view(-1)>0)== y_batch).sum().item()
total += y_batch.size(0)print(f'Epoch {epoch +1}/{num_epochs}, Loss: {epoch_loss / total:.4f}, Accuracy: {correct / total:.4f}')
7. 测试SNN模型
训练完成后,我们可以使用一些新的数据样例来测试我们的SNN模型:
# 生成测试数据
X_test = torch.randn(10,2)
y_test =(X_test[:,0]+ X_test[:,1]>0).float()# 测试模型with torch.no_grad():
outputs = model(X_test)
test_loss = criterion(outputs.view(-1), y_test)
test_accuracy =((outputs.view(-1)>0)== y_test).sum().item()/ y_test.size(0)print(f'Test Loss: {test_loss:.4f}, Test Accuracy: {test_accuracy:.4f}')
8. 总结
本文主要介绍了脉冲神经网络(SNN)的基本原理,并使用PyTorch框架搭建了一个简单的SNN模型。我们使用一些数据样例进行训练和测试,展示了SNN模型的性能。SNN具有较高的计算效率和能量效率,在某些应用场景中具有较大的潜力。
版权归原作者 微学AI 所有, 如有侵权,请联系我们删除。