表达式转换-中缀转后缀表达式后计算-数据结构与算法

文章目录

问题

一个计算中缀表达式的算法题

40分，其余六个测试点都显示"read(ASCII 13)"
我的代码现在一直只能过第1、6、7、8这四个测试集，
查看测试集显示错误信息：
“Wrong Answer.wrong answer On line 1 column 25, read (ASCII 13), expected +.”

题目链接：表达式转换-洛谷

我查了(ASCII 13)是回车键，但是我又能过四个测试集，为什么输出会有回车键的问题呢？

谁能救救我啊？万分感谢！

下面是我的代码（可能有点乱，抱歉）：

/*long long
1）输入数字是单个数字
2）输入没有负数 */#include<iostream>#include<cstdio>#include<stack>usingnamespace std;constint max0 =500;
stack<char> s;//计算后缀表达式用 longlongget_num();//从栈中返回一个整型数字 boolcompare_sign(char big,char small);//比较两个(四则运算符)运算符的优先级 voidchange(char str[]);//给新转化出来的后缀表达式 操作数 加分隔符'.'voidout_bds(char str[],int i, stack<char> ss);//输出中间产物表达式intmain(){char a[max0]{};//后缀表达式 intac(0);//迭代a
    stack<char> sign;//符号栈char m[max0]{};//待处理的中缀表达式charch(0);for(int i =0; i < max0;++i){
        ch =getchar();if(ch =='\n')break;
        m[i]= ch;}//--------------------一、中缀表达式转后缀表达式 for(int i =0; i < max0 && m[i]!='\0'; i++){//读取中缀表达式并开始转换 if('0'<= m[i]&& m[i]<='9'){//遇到操作数，直接加入后缀表达式 
            a[ac++]= m[i];}elseif(m[i]!='('&& m[i]!=')'){while(!sign.empty()&&compare_sign(sign.top(), m[i])){ 
                a[ac++]= sign.top();//遇到运算符，出栈优先级不小于它的运算符加入表达式，直到栈空或遇到'('
                sign.pop();}
            sign.push(m[i]);}//然后自己入栈 elseif(m[i]=='('){
            sign.push(m[i]);}elseif(m[i]==')'){//遇到')'，出栈加入表达式直到'(' while(sign.top()!='('){
                a[ac++]= sign.top();
                sign.pop();}
            sign.pop();}}while(!sign.empty()){//出栈所有剩余运算符 
        a[ac++]= sign.top();
        sign.pop();}change(a);out_bds(a,0, s);//--------------------二、计算后缀表达式 chart(0); ac =0;while(true){
        t = a[ac++];//入栈 if(t =='@'){s.pop();break;}
        s.push(t);if(t =='+'|| t =='-'|| t =='*'|| t =='/'|| t =='^'){//见运算符
            s.pop();//出栈运算符longlongd(0),b(0);//出栈两个数字为int型
            s.pop(); d =get_num();
            s.pop(); b =get_num();longlongresult(1);//计算if(t =='+') result = b + d;elseif(t =='-') result = b - d;elseif(t =='*') result = b * d;elseif(t =='/') result = b / d;elseif(t =='^'){for(int i =0; i < d;++i)
                    result *= b;}if(result <0){s.push('0'); result =-result;}
            stack<char> c;//结果转为char型再入栈if(result ==0){s.push('0');}while(result !=0){
                c.push((char)(result %10+'0'));
                result /=10;}while(!c.empty()){
                s.push(c.top());
                c.pop();}
            s.push('.');out_bds(a, ac, s);}}return0;}//----------------------------------------//只考虑了表达式转换过程中可能发生的优先级比较 boolcompare_sign(char big,char small){if(big =='+'|| big =='-'){if(small =='+'|| small =='-')returntrue;}elseif(big =='*'|| big =='/'|| big =='^'){if(small !='('&& small !='^')returntrue;}returnfalse;}//----------------------------------------//从char型栈中读取出一个int型操作数 longlongget_num(){longlongsum(0);chart(0);for(longlong i =1; s.top()!='.'; i *=10){//i也是必须开long long的 
        t = s.top();
        sum +=(longlong)(s.top()-'0')* i;
        s.pop();if(s.empty())break;}if(t =='0') sum =-sum;return sum;}//----------------------------------------//从char型栈中读取出一个int型操作数;out_bds()的配套 longlongget_num(stack<char>&ss){longlongsum(0);chart(0);for(longlong i =1; ss.top()!='.'; i *=10){    t = ss.top();
        sum +=(longlong)(ss.top()-'0')* i;
        ss.pop();if(ss.empty())break;}if(t =='0') sum =-sum;return sum;}//----------------------------------------//给新转化出来的后缀表达式 操作数 加分隔符'.'voidchange(char str[]){char t[max0]{};inttc(0);for(int i =0; str[i]!='\0'; i++){if('0'<= str[i]&& str[i]<='9'){
            t[tc++]= str[i];
            t[tc++]='.';}else t[tc++]= str[i];}for(int i =0; t[i]!='\0'; i++) 
        str[i]= t[i];
    str[tc]='@';}//表达式结束符//----------------------------------------//输出中间产物表达式，从str[i]开始;参数建立了一个副本栈，不担心原s改变 voidout_bds(char str[],int i, stack<char> ss){
    stack<longlong> t;//中转站 while(ss.empty()==0){if(ss.top()=='.')
            ss.pop();
        t.push(get_num(ss));}while(t.empty()==0){
        cout << t.top()<<" ";
        t.pop();}for(; str[i]!='\0'; i++){if(str[i]!='.'&& str[i]!='@') 
            cout << str[i]<<" ";}
    cout << endl;}/*
测试集
8-(3+2*6)/5+4
9+(9^8+(9^8+(9^8+(9^8))))
*/

程序运行：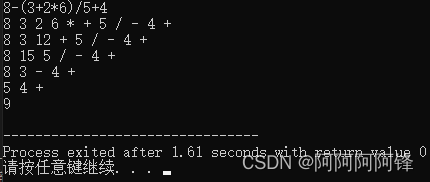

经验总结

• 注意创建的数组大小，题目说输入字符串长度不超过100，但是表达式计算过程中的中间结果是可能超过100的。
• 注意不要变量名冲突。
• 仔细审题，有些坑很细，如：计算过程总数字不超过231，但是可能等于，那int类型就不够了。
• 如果重载了函数，修改其中一个时可能其它的也需要修改
• 输出格式其实挺烦的，有时题目不会说很清楚，甚至就必须有行末空格。