本节介绍稳定性分析的原理以及代数稳定性判据(劳斯判据)
本节介绍系统稳态误差的定义及计算方法
本节介绍时域校正方法
文章目录
以下内容,均针对线性系统
稳定性分析
稳定性的定义:
在扰动作用下系统偏离了原来的平衡状态,如果扰动消除后,系统能够以足够的准确度恢复到原来的平衡状态,则系统是稳定的。否则系统不稳定。
稳定的充要条件与必要条件
充要条件
扰动发生后要求回到原来的平衡状态,也就是单位脉冲响应为0。(认为单位脉冲为典型扰动输入)
lim
t
→
∞
k
(
t
)
=
0
\lim \limits_{t\rightarrow \infty}k(t)=0
t→∞limk(t)=0

c
i
c_i
ci是
s
=
−
p
i
s=-p_i
s=−pi处的留数。因此
lim
t
→
∞
k
(
t
)
=
0
\lim \limits_{t\rightarrow \infty}k(t)=0
t→∞limk(t)=0的充要条件是:特征根具有负实部,也就是系统的**闭环极点全部位于左半s平面**
必要条件

控制系统稳定的必要条件是:特征方程的各项系数具有相同的符号,且都不为0
在计算代数稳定判据之前可以先行做初步判断
劳斯判据-Routh
列出劳斯表:
特征方程各项按照幂次从高到低排序,劳斯表第一行是奇数项(第1,3,5,7,9项)系数。第二行是偶数项(第2,4,6,8,10项)系数。
之后第x行的第y个元素等于
−
1
第
x
−
1
行的第一个元素
⋅
第
x
−
1
和
x
−
2
行的第
1
和第
i
+
1
个元素组成的行列式
-\frac{1}{第x-1行的第一个元素}\cdot 第x-1和x-2行的第1和第i+1个元素组成的行列式
−第x−1行的第一个元素1⋅第x−1和x−2行的第1和第i+1个元素组成的行列式
计算到最后s1、s0的时候,劳斯表一行只有一个元素。可以通过这个检查是否计算正确。
劳斯判据 :劳斯表第一列元素符号改变次数=特征方程在右半平面内的根的个数。
因此,当劳斯表第一列元素具有相同的符号,则系统稳定。
在计算时,某一行元素同时乘或除某一个数不影响最终的稳定性结论,因此遇到分数或者过大的数,可以先去分母\约分处理以简化运算。(后面例题为了直观并没有这样操作)
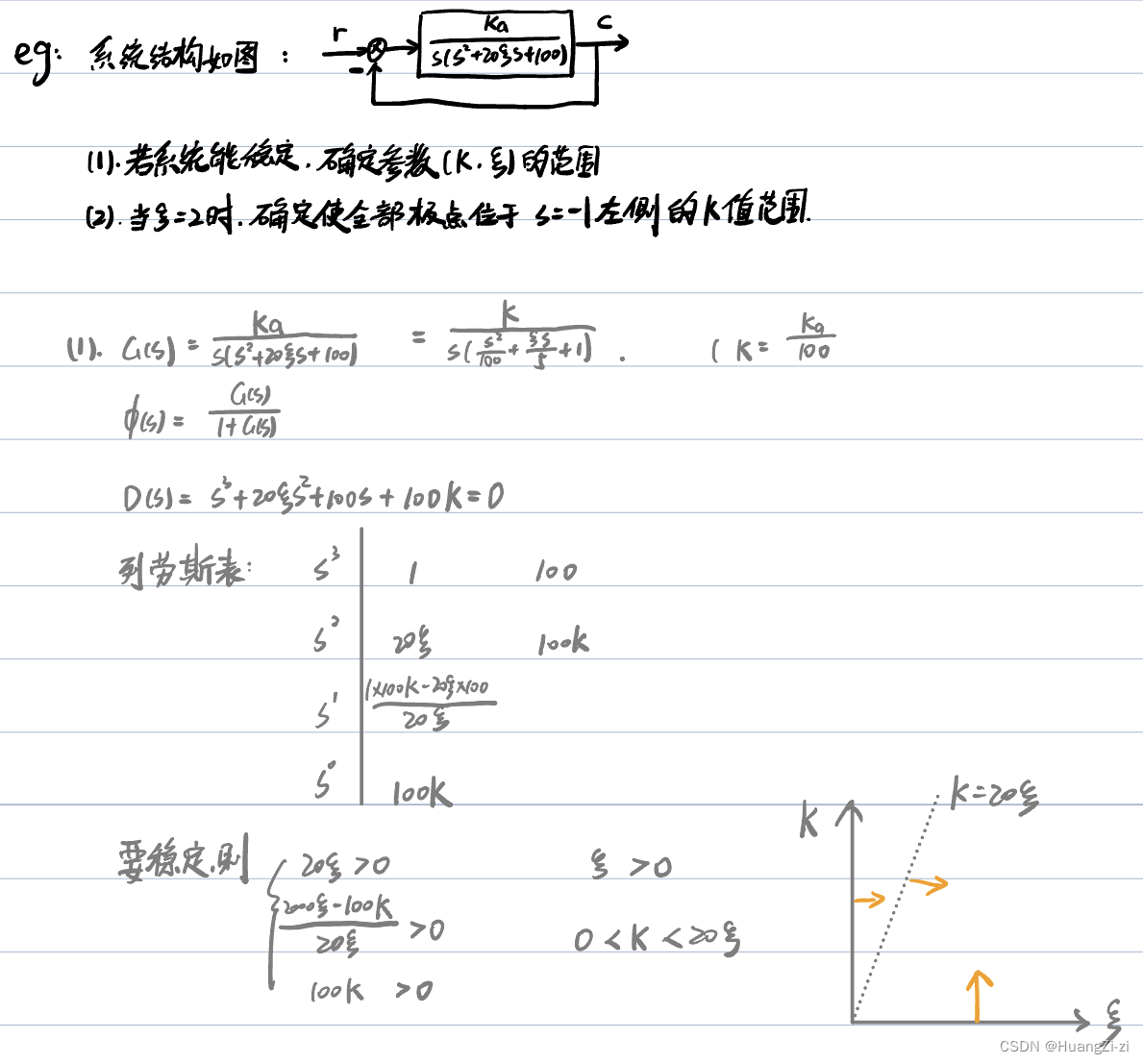
例题
- 用劳斯判据判断系统是否稳定
 判断稳定性的题,如果没有特殊要求一定先看是否满足必要条件。如果过不满足那么可以直接结论不稳定。
判断稳定性的题,如果没有特殊要求一定先看是否满足必要条件。如果过不满足那么可以直接结论不稳定。 - 用劳斯判据确定参数范围

两种特殊情况
某行的第一列为0,但这一行不全为0
使用一个很小的正数
ε
\varepsilon
ε代替0,继续运算

某一行全部为0
用上一行元素构建辅助方程,对s求导一次,用新方程的系数代替全零行的系数继续运算
出现全零行的一定是奇次行。
出现全零行有可能是:特征方程有以原点对称的实根、以原点对称的虚根、以虚轴对称的共轭复根。具体是哪一种,需要令辅助方程=0,求解。
问题辨析
- 系统稳定性是系统自身的属性,与输入的类型、形式无关
- 系统是否稳定,只取决于闭环极点,与闭环零点无关。(闭环零点影响动态性能,但不影响稳定性。闭环极点决定系统稳定性,也影响动态性能)补:增加闭环零点:峰值时间靠前,超调量增大 增加闭环极点:峰值时间靠后,超调量减小
- 闭环系统稳定性与其开环是否稳定无关
稳态误差
稳态误差是系统的稳态性能指标,是对系统控制精度的度量。
误差包括永久性误差,比如由于参数漂移、元件老化等带来的误差,还有原理性误差,即由于系统结构、参数引入的误差。这里只讨论原理性误差
通常把阶跃输入下没有原理性稳态误差的系统称为无差系统,反之称为有差系统
误差与稳态误差的定义
- 按输入端定义的误差
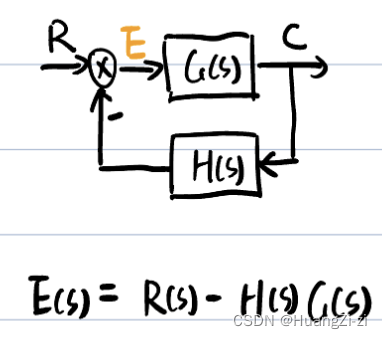
- 按输出端定义的误差
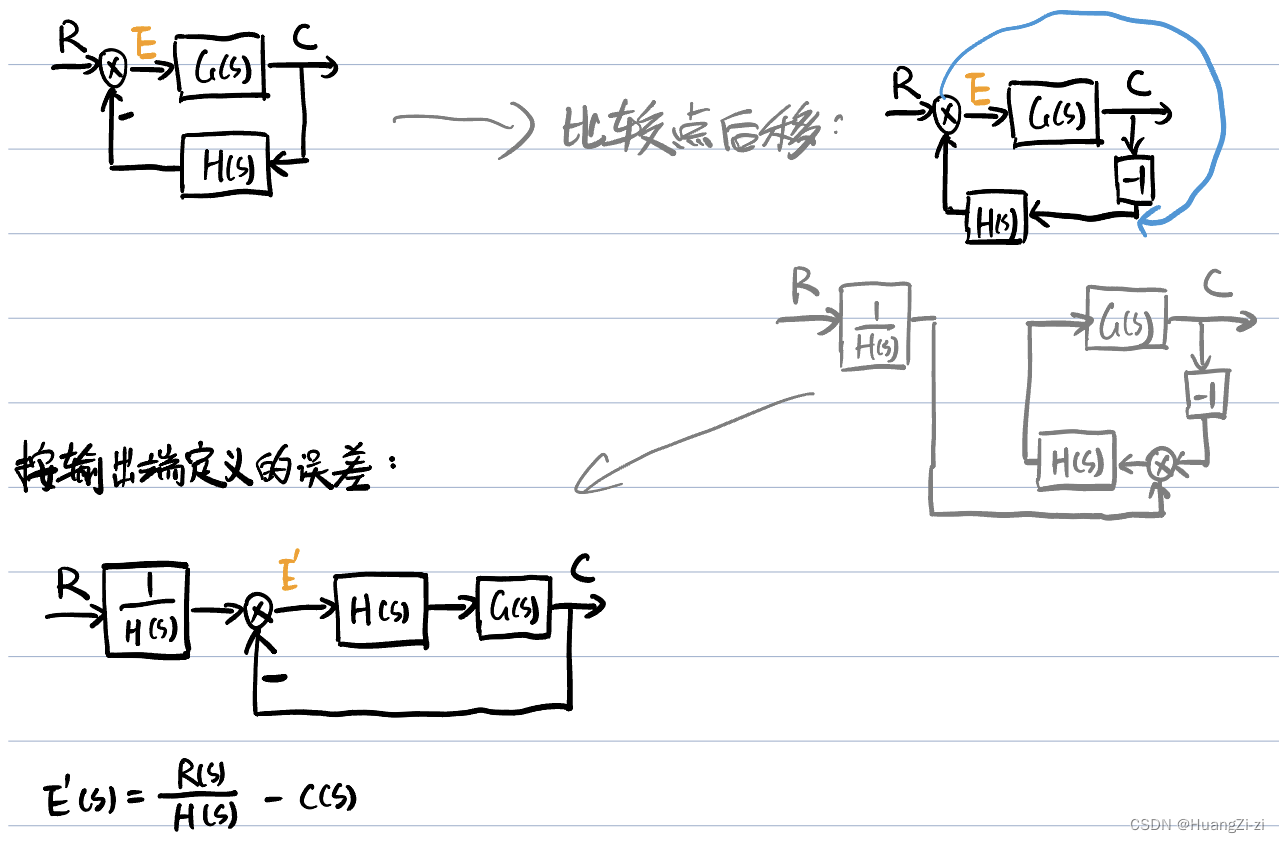 两种定义本质上是一样的,如果再进一步推导,就有: E ′ ( s ) = E ( s ) H ( h ) E'(s)=\displaystyle \frac{E(s)}{H(h)} E′(s)=H(h)E(s)
两种定义本质上是一样的,如果再进一步推导,就有: E ′ ( s ) = E ( s ) H ( h ) E'(s)=\displaystyle \frac{E(s)}{H(h)} E′(s)=H(h)E(s)
以下的分析都是基于输入端定义的误差进行的。
- 稳态误差 误差传递函数: Φ e = E ( s ) R ( s ) \Phi_e=\displaystyle \frac{E(s)}{R(s)} Φe=R(s)E(s) e ( t ) = L − 1 [ E ( s ) ] = r ( t ) − c ( t ) e(t)=\mathscr{L}^{-1}[E(s)]=r(t)-c(t) e(t)=L−1[E(s)]=r(t)−c(t) 由于系统输出分为暂态分量和稳态分量,因此误差也分为暂态分量和稳态分量: e ( t ) = e t s ( t ) + e s s ( t ) e(t)=e_{ts}(t)+e_{ss}(t) e(t)=ets(t)+ess(t) ts->temporary state ss->stable state, e s s = lim t → ∞ e ( t ) = e ( ∞ ) e_{ss}=\lim \limits_{t \rightarrow \infty}e(t)=e(\infty) ess=t→∞lime(t)=e(∞) 系统的稳态误差就是误差的稳态分量
计算稳态误差的一般方法
- 判断系统稳定性「这一点非常重要,因为只有对稳定的系统研究稳态误差才有意义」
- 求误差传递函数「可以用梅逊公式快速得结果」
- 用终值定理求稳态误差
来看一道例题: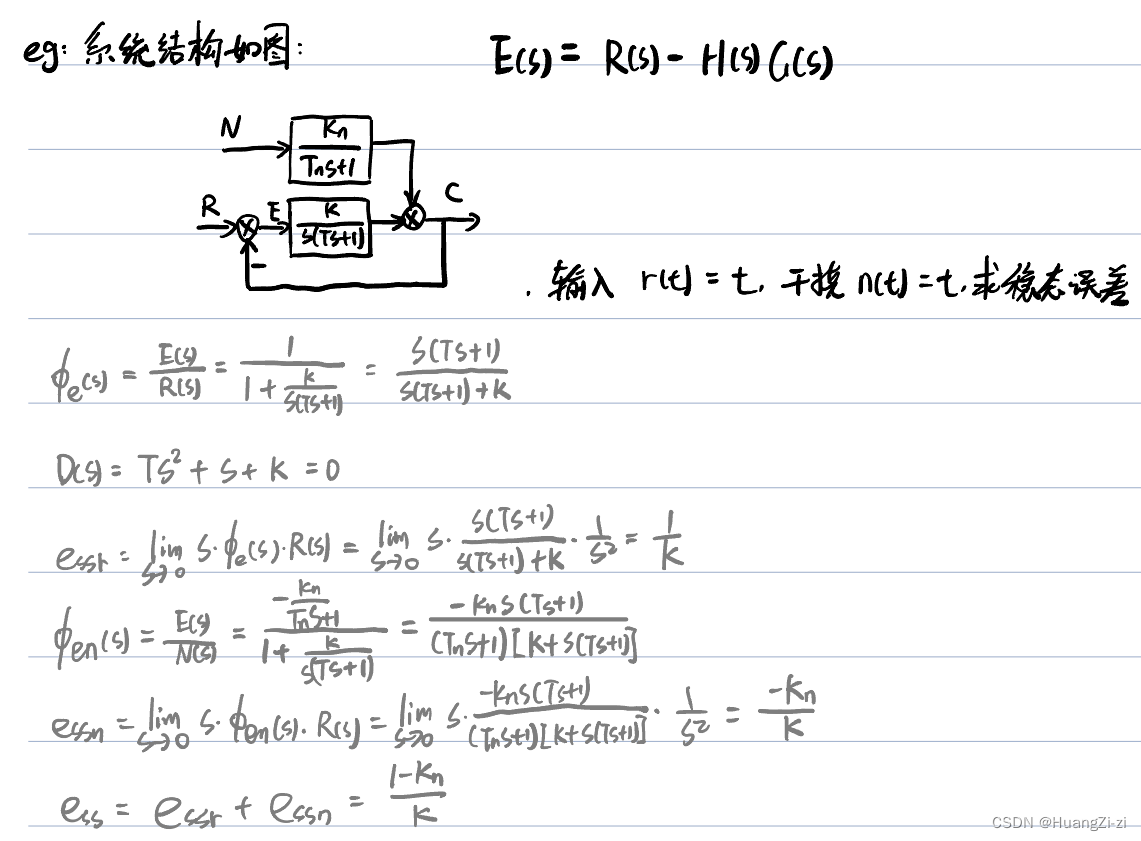
一般方法虽然实用但一般不会使用它。下面介绍静态误差系数法:
静态误差系数法
构建如下的系统: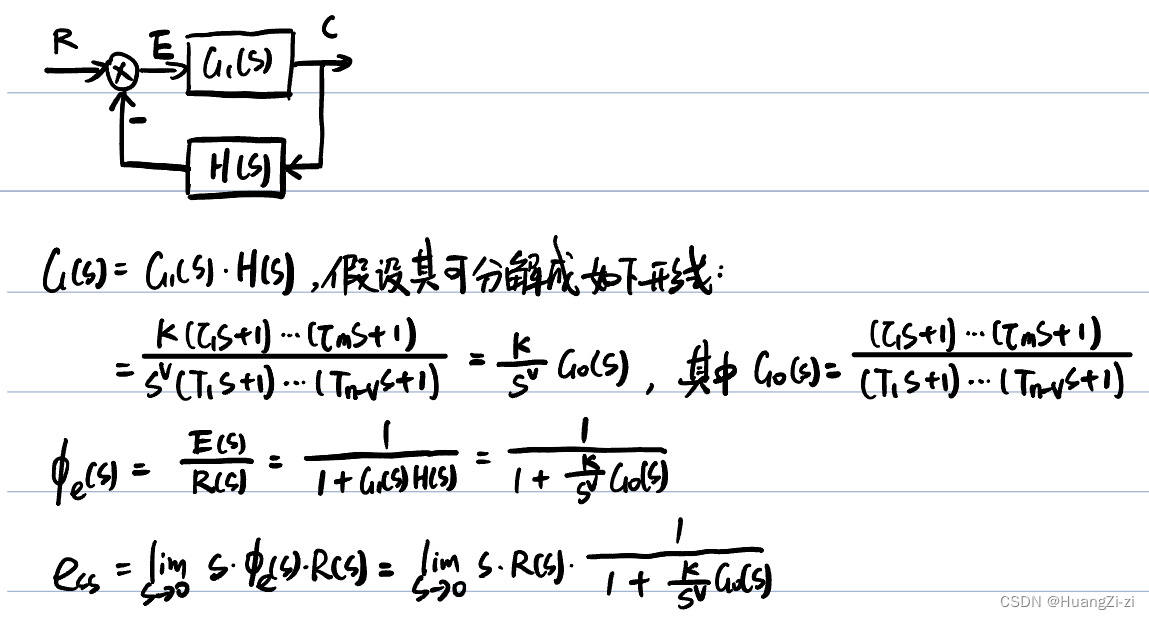
开环传递函数
G
(
s
)
=
K
s
v
G
0
(
s
)
G(s)=\frac{K}{s^v}G_0(s)
G(s)=svKG0(s)
G0化成尾1标准型所以K是开环增益
v是系统型别(就是一个分类标准,v=0叫做0型,v=1叫做1型)
仍然使用一般方法计算稳态误差。
根据不同的输入,分别代入求解,由此引出静态位置误差系数、静态速度误差系数、静态加速度误差系数的定义。
再根据不同的系统型别,分别计算出三个静态误差系数:
型别vKpKvKa0K001
∞
\infty
∞K02
∞
\infty
∞
∞
\infty
∞K
再带回,计算系统的稳态误差:
型别vesspessvessa0
A
1
+
K
\frac{A}{1+K}
1+KA
∞
\infty
∞
∞
\infty
∞10
A
K
\frac{A}{K}
KA
∞
\infty
∞200
A
K
\frac{A}{K}
KA
有了这两个表,就可以很方便的计算系统的误差了,来看一道例题:
例题2: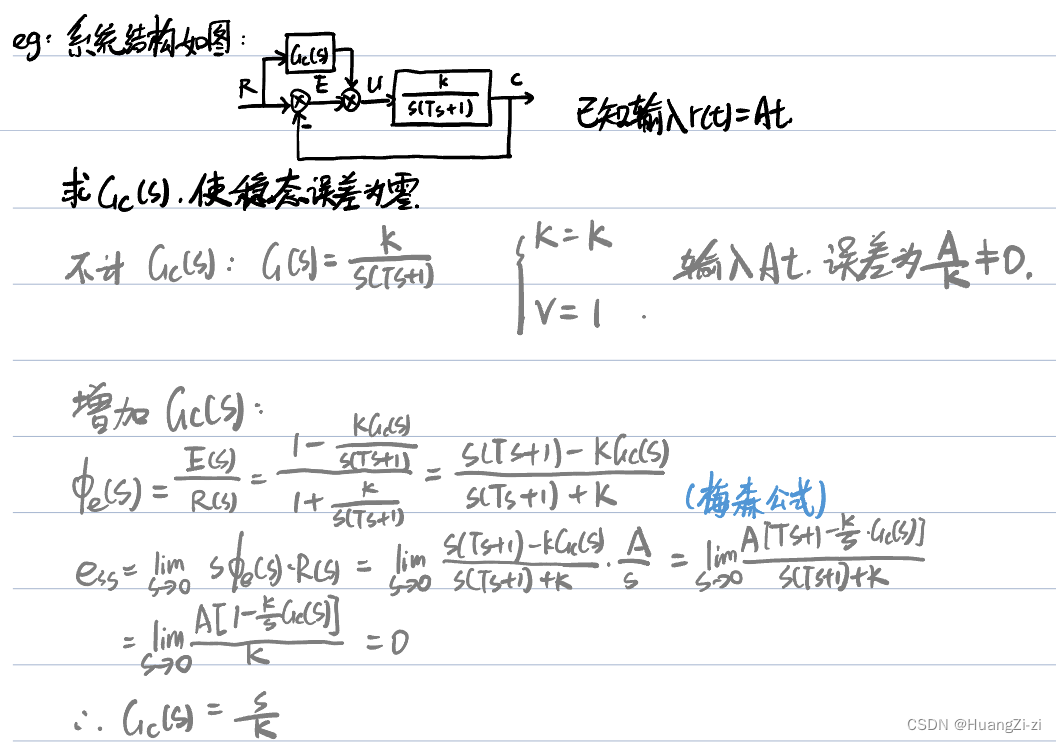
从这道例题里面可以看出:按前馈补偿的复合控制方案可以提高系统的稳态精度
例题3: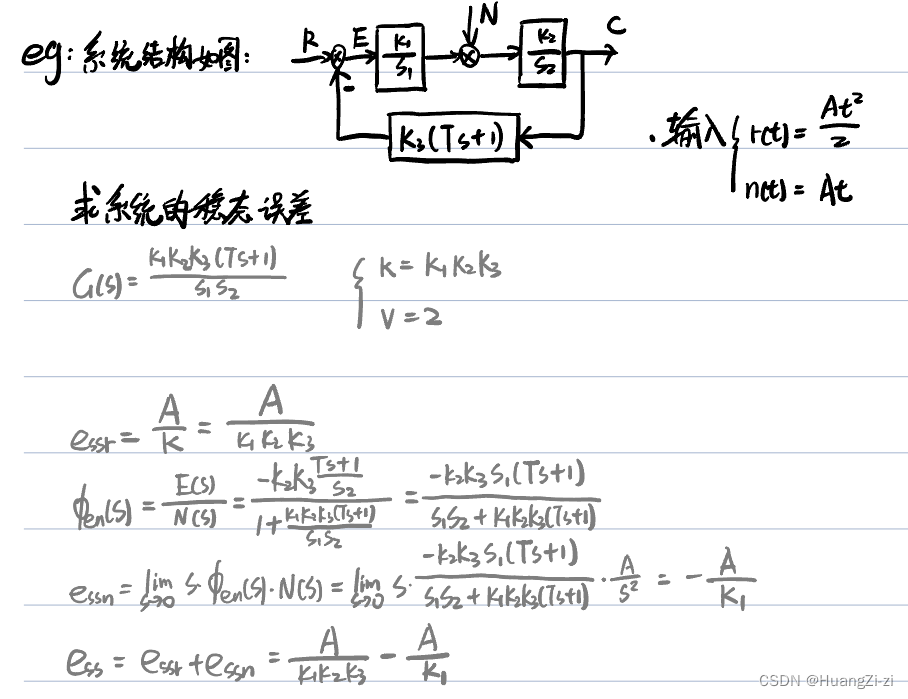
从这道例题可以看出:在主反馈口到干扰作用点之前的前向通道中提高增益、引入积分环节,可以同时减小或消除输入和干扰作用下产生的稳态误差。。
例题4:
在这道例题里面,我们一定注意,在计算稳态误差等等性能指标之前,一定确定系统是稳定的。尤其是这种需要自定义参数的题目。
动态误差系数法
静态误差系数法只能求出最终的误差稳态值ess。而使用动态误差系数法可以研究误差中的稳态分量es(t)随时间的变换规律
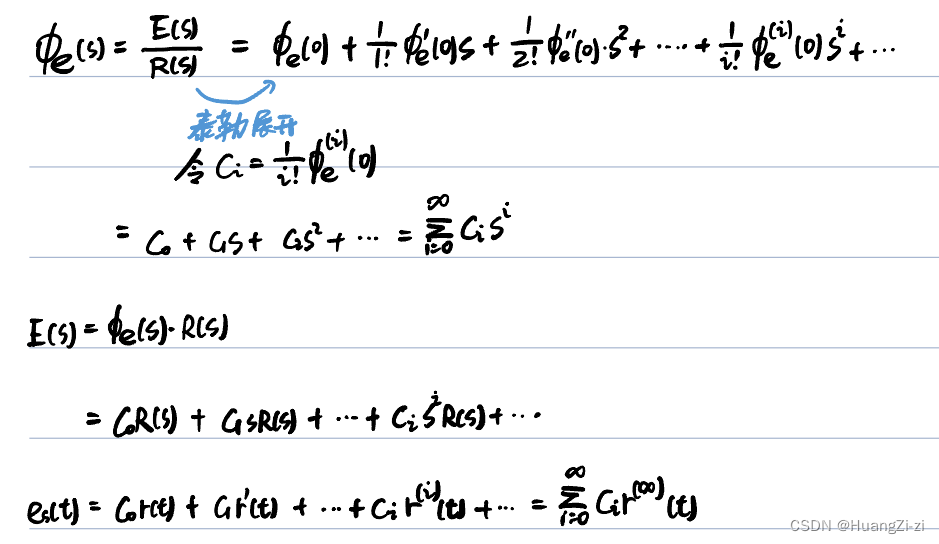
首先把误差传递函数展开,称E(s)的泰勒展开为误差级数。
C
i
=
1
i
!
Φ
e
(
i
)
(
0
)
C_i=\frac{1}{i!}\Phi_e^{(i)}(0)
Ci=i!1Φe(i)(0),称
C
i
C_i
Ci为**动态误差系数**
按照定义来算的话,
C
i
=
1
i
!
Φ
e
(
i
)
(
0
)
C_i=\frac{1}{i!}\Phi_e^{(i)}(0)
Ci=i!1Φe(i)(0)但是这样的计算方法比较繁琐所以一般使用长除法:
(将开环传递函数按升幂排列才能除出级数的形式)
这个问题需要注意的是,即使稳态误差是无穷大,控制系统仍然是可用的。比如导弹的控制系统,导弹打出去几分钟就爆炸了,那么只要在这几分钟之内误差满足要求就好了。
扰动作用下的稳态误差
之前的讨论是从输入端直接有输入时造成的干扰。而接下来单独讨论某一个特定的扰动作用下产生的稳态误差。
其实分析方法都是一样的,使用的是动态误差系数法。不同在于传递函数变成了误差传递函数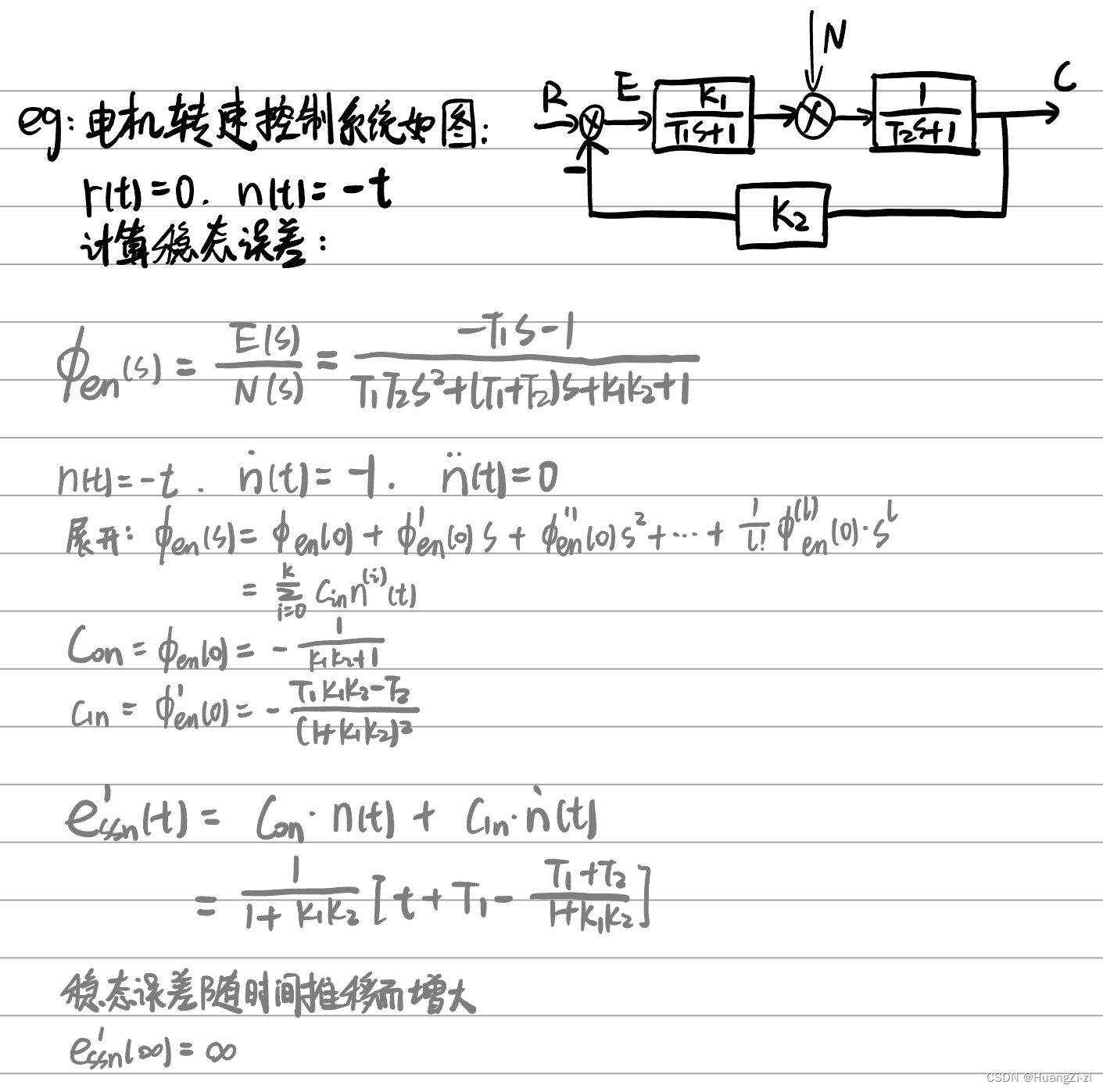
时域校正
校正:采用适当的方式,在系统中加入一些校正装置,用以改善系统性能,使系统满足指标要求。
校正装置:结构和参数可调整的装置
校正方式:串连校正、反馈校正、复合校正
时域校正不怎么常用,了解即可
反馈校正
反馈的作用:
局部正反馈可以提高环节增益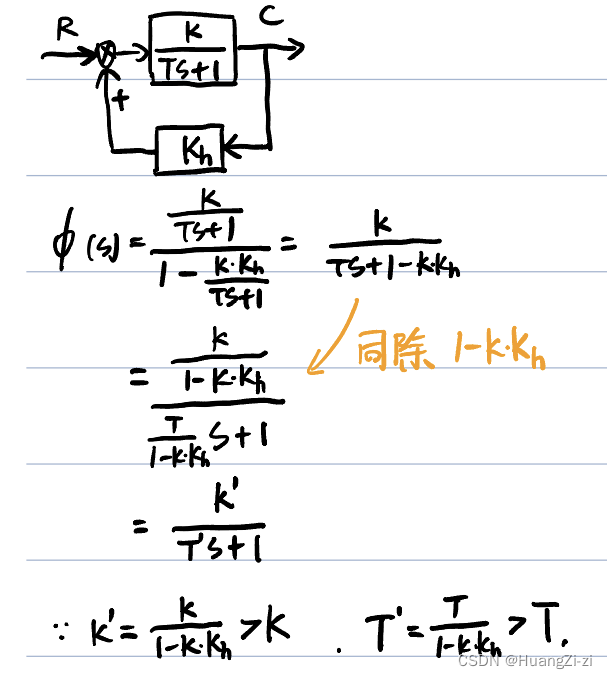
增加局部正反馈之后系统增益变大,调节时间变长。

增加局部反馈之前,系统不稳定。而增加这个反馈之后系统变得稳定,也就是被校正了。
复合校正
复合校正就是串联校正加上反馈校正。串连校正前面没有讲过,其实就是加一个环节。
看下面这个例题:
在这道题里面,G1G2属于前馈校正元件,K1是串连校正元件的增益,
1
s
\frac{1}{s}
s1是反馈校正元件。
版权归原作者 HuangZi-zi 所有, 如有侵权,请联系我们删除。