leetcode刷题之轮转数组（三种方法刷爆力扣）

大家好啊，我是小生啊🙈🙈🙈
我可没忘记带着大家刷题呢，嘿嘿兄弟姐妹们，我来啦😎😎😎让我们开始我们今天快乐的力扣刷题之旅吧，啦啦啦~~~ 😝😜😙

🌞🌞🌞 让我们一题多解，刷爆力扣，冲冲冲👊👊👊

力扣练习：轮转数组🏃🏃🏃

一.🏠题目描述

** 嘿嘿，兄弟们，老规矩，直接看题：** 🙊 🙊 🙊

示例1：
输入：nums = [1,2,3,4,5,6,7], k = 3
输出：[5,6,7,1,2,3,4]
示例2：
输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]

二.🏠题目分析

兄弟们，这道题目可是力扣里面中等难度的题目呢，我们要好好对待，一定能大有所获的，加油加油！！！😉😉😉
老规矩啦，一定要读懂题目哦，官方为了让大家理解，特地写这个数组轮转的结果，我们来看一下。
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

三.🏠解决方法

1.🚀思路一：化尾为头再循环挪动

既然我们这里数组每次轮转时将数据往后挪动，那我们不妨 用一个临时变量把数组最后一个元素存储起来存储起来，接着通过循环将其他前面的数组元素一次往后移动一位，最后把临时变量存储的数据放到数组的开头。也许你觉得小生说得不太清楚，那小生画一张图片让大家理解一下😎😎😎

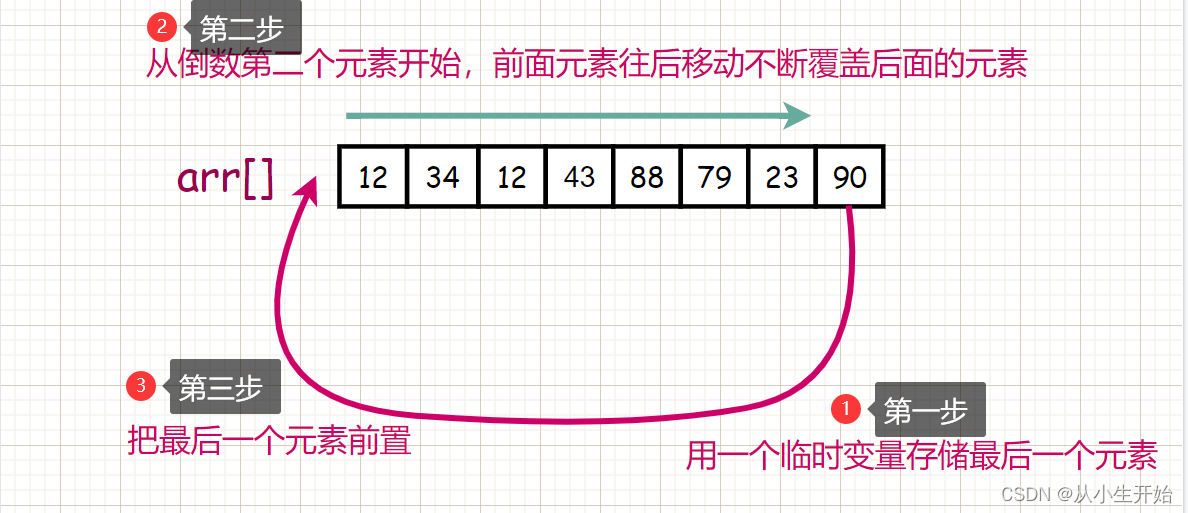
都到这里了，相信大家都能理解这种思路了，但是这种每次向右边轮转数组，所有的值就要往后挪一次，时间复杂度较大，那我们有没有什么方法把他优化一下呢？😖😖😖我们看接下来的思路二。😃😃😃

2.🚀思路二：开辟新空间优化时间

前面我们已经说过了，我们要轮转K次，按照之前的方法每次轮转我们都得进行一次移动位置，那我们为什么不选择一次性移位呢？我们可以仔细思考一下，向右轮转K次就是把数组倒数第K个数放到其他数组元素的前面，我们可以用新的数组把这两部分按照后来的顺序存储即可，因此，从空间复杂度的角度来看，该方法的空间复杂度更大，但是从时间复杂度的角度来探讨，确实是优化了许多。同样的道理，小生直接画个图让大家理解一下,画图可累死小生了~~~😭😭

到了这里我们完成了一半啦，接着往下看：👀👀👀

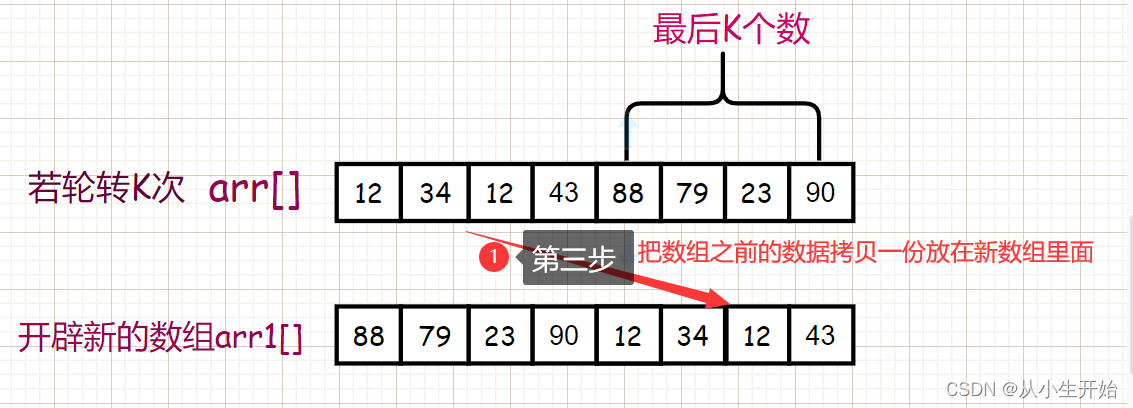
最后将新数组的元素再拷贝一份放入原数组就可以了。但是如果K大于数组最大的长度的时候我们会发现出现问题，因此我们待会需要处理一下。

3.🚀思路三：三次逆置(大神方法)

先声明，这种方法小生这种菜鸟可想不到，友友们，千万别说我是大佬，我真的是小菜鸟。我们来看看大神的方法，假设我们设为该数组一共有N个元素，轮转K次大神是这样做的，先把后K个数组元素逆置，再把前N-K个数组元素逆置，最后把这个数组来个整体逆置。为了方便大家理解，小生再画个图吧。

跟着思路走下去💪💪💪

最后我们发现竟然真的成功了，不愧是大神的方法，时间复杂度和空间复杂度都优化了。思路我们分析好了让我们直接上代码吧。

四.🏠代码实现

1.🚀方法一代码详解

按照我们之前分析的思路，每次轮转时用临时变量存储元素最后一个元素，然后再把其他元素往后覆盖。直接代码走起来👇👇👇👇

voidrotate(int* nums,int numsSize,int k){//因为数组轮转是由周期的，我们可以通过一下方法简化问题
    k %= numsSize;for(int i =0; i < k; i++){//定义临时变量存放最后一个元素int tmp = nums[numsSize -1];//从倒数第二个元素开始从前往后不断覆盖for(int j = numsSize -1; j >0; j--){
            nums[j]= nums[j -1];}//把tmp的值拷贝一份给num[0]
        nums[0]= tmp;}}

2.🚀方法二代码详解

开辟内存空间相同的新数组，把后k个元素按顺序放到新数组再把之前的数组放入新数组， 再把最后将新数组元素拷贝回原数组。、
代码如下 👇👇👇

voidrotate(int* nums,int numsSize,int k){//开辟一个和原数组内存大小相同的新数组newnumsint* newnums =(int*)malloc(sizeof(int)*numsSize);for(int i =0; i < numsSize; i++){//把每个元素放到新开辟的数组的轮转 k 步后的位置
       newnums[(i + k)% numsSize]= nums[i];}//将新数组的元素拷贝回原数组for(int i =0; i < numsSize; i++){
       nums[i]= newnums[i];}free(newnums);
   newnums =NULL;}

3.🚀方法三代码详解

** 我们可以先构造一个逆置函数，那如何实现逆置呢？我们只需要用两个下标的增加和减少不断往中间靠近，最后只有两种情况，当numsize为奇数时，临界为left=right，当两个数是偶数时，最后临界为left>right，因此我们循环的条件为left<right即可。**
废话不多说，直接上干货👇👇👇

//构造逆置函数voidinvert(int*nums,int left,int right){//当left>=right循环停止while(left<right){//交换nums[left]和nums[right]的值int num = nums[left];
       nums[left]= nums[right];
       nums[right]= num;//两个下标不断靠拢
       left++;
       right--;}}voidrotate(int* nums,int numsSize,int k){//判断是否超过数组元素个数if(k>numsSize){
       k=k%numsSize;}//把后k个元素逆置invert(nums,numsSize-k,numsSize-1);//把前数组前K个元素逆置invert(nums,0,numsSize-k-1);//整体逆置invert(nums,0,numsSize-1);}

五. 🏠结语

如果你能看到这里那就说明你已经是一个很厉害的人啦 😆😆😆
如果觉得对你有帮助的话，别忘了关注一下小生哦，小生会不断更新更加优质的内容的，加油技术人 😃😃😃