隐私信息检索方案（PIR）——基于同态加密的PIR的实现安全查询。小白可复现

1什么是隐私信息检索

隐私信息检索是指在保护用户隐私的前提下，通过各种技术手段和方法来获取用户所需的信息。即保护的根本是我的查询需求。

1.1在实际应用例子

假设银行A有一潜在贷款客户小张，银行A为了足够多的了解小张的信用情况，希望向其他多家银行查询小张贷款情况或信用记录。但因为害怕其他银行抢走该客户，所以银行A不希望泄露自己在查询小张这一事实。

1.2可搜索加密和隐私信息检索的区别

可搜索加密技术。顾名思义，可搜索加密就是在加密的情况下实现搜索功能，常用于云计算当中。可搜索加密应用示例如图所示，能够实现将用户的数据进行特殊的加密后上传云服务器上, 并且可以实现根据关键字进行检索的功能。

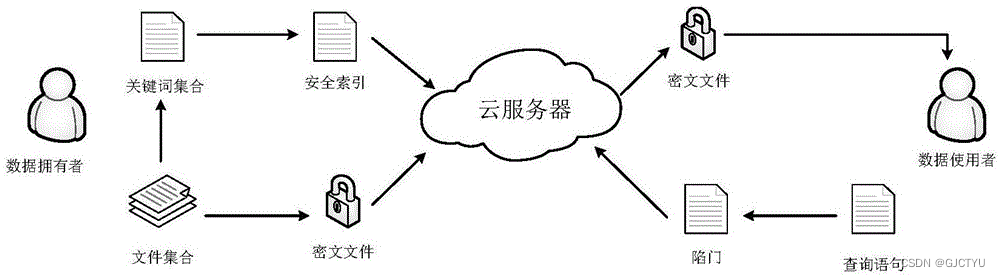
对于第三方敌手或者服务器只知道用户发给的加密关键词索引和密文数据，整个过程中云服务器不知道检索关键字（keyword3）和检索结果（数据3）对应的原始明文是什么。但是，数据拥有者监听到检索结果的话，可以直接解密并得到对应的明文。即可搜索加密技术仅能阻止云服务器或外部敌手获得用户查询隐私，不能阻止数据拥有者获得用户查询隐私。信息检索是从数据拥有者的角度出发，确保用户的隐私得到有效保护。

2基于paillier同态加密的PIR实现

2.1何为同态加密（HE）？

很多小伙伴对于paillier肯定非常了解了，但是本博主还是介绍一下吧。懂得宝宝直接跳过就行

HE是一种特殊的加密方法，它允许直接对加密数据执行计算，如加法和乘法，而计算过程不会泄露原文的任何信息。计算的结果仍然是加密的，拥有密钥的用户对处理过的密文数据进行解密后，得到的正好是处理后原文的结果。

根据支持的计算类型和支持程度，同态加密可以分为以下三种类型：

• 半同态加密（Partially Homomorphic Encryption, PHE）：只支持加法或乘法中的一种运算。其中，只支持加法运算的又叫加法同态加密（Additive Homomorphic Encryption, AHE）；
• 部分同态加密（Somewhat Homomorphic Encryption, SWHE）：可同时支持加法和乘法运算，但支持的计算次数有限；
• 全同态加密（Fully Homomorphic Encryption, FHE）：支持任意次的加法和乘法运算

2.2Paillier：最著名的半同态加密方案

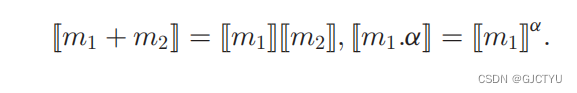
stepup：密钥生成

1. 随机选择两个大素数 𝑝,𝑞 满足 𝑔𝑐𝑑(𝑝𝑞,(𝑝−1)(𝑞−1))=1 ，且满足 𝑝,𝑞 长度相等
2. 计算 𝑛=𝑝𝑞 以及 𝜆=𝑙𝑐𝑚(𝑝−1,𝑞−1) ，这里 𝑙𝑐𝑚 表示最小公倍数， |𝑛| 为 𝑛 的比特长度
3. 随机选择整数 𝑔←𝑍𝑛2∗
4. 定义 𝐿 函数： 𝐿(𝑥)=𝑥−1𝑛 ，计算 𝜇=(𝐿(𝑔𝜆mod𝑛2))−1mod𝑛

公钥： ，(𝑛，𝑔) ，私钥： (𝜆,𝜇)

step1：加密

1. 输入明文消息 𝑚 ， 满足 0≤𝑚<𝑛
2. 选择随机数𝑟 满足 0≤𝑟<𝑛 且 𝑟∈𝑍𝑛∗
3. 计算密文 𝑐=𝑔𝑚𝑟𝑛mod𝑛2

step2：解密

1. 输入密文 𝑐 ，满足 𝑐∈𝑍𝑛2∗
2. 计算明文消息 𝑚=𝐿(𝑐𝜆mod𝑛2)⋅𝜇mod𝑛

2.3基于同态加密的PIR实现

举个例子:

服务端数据
索引数据1m12
m2
3m3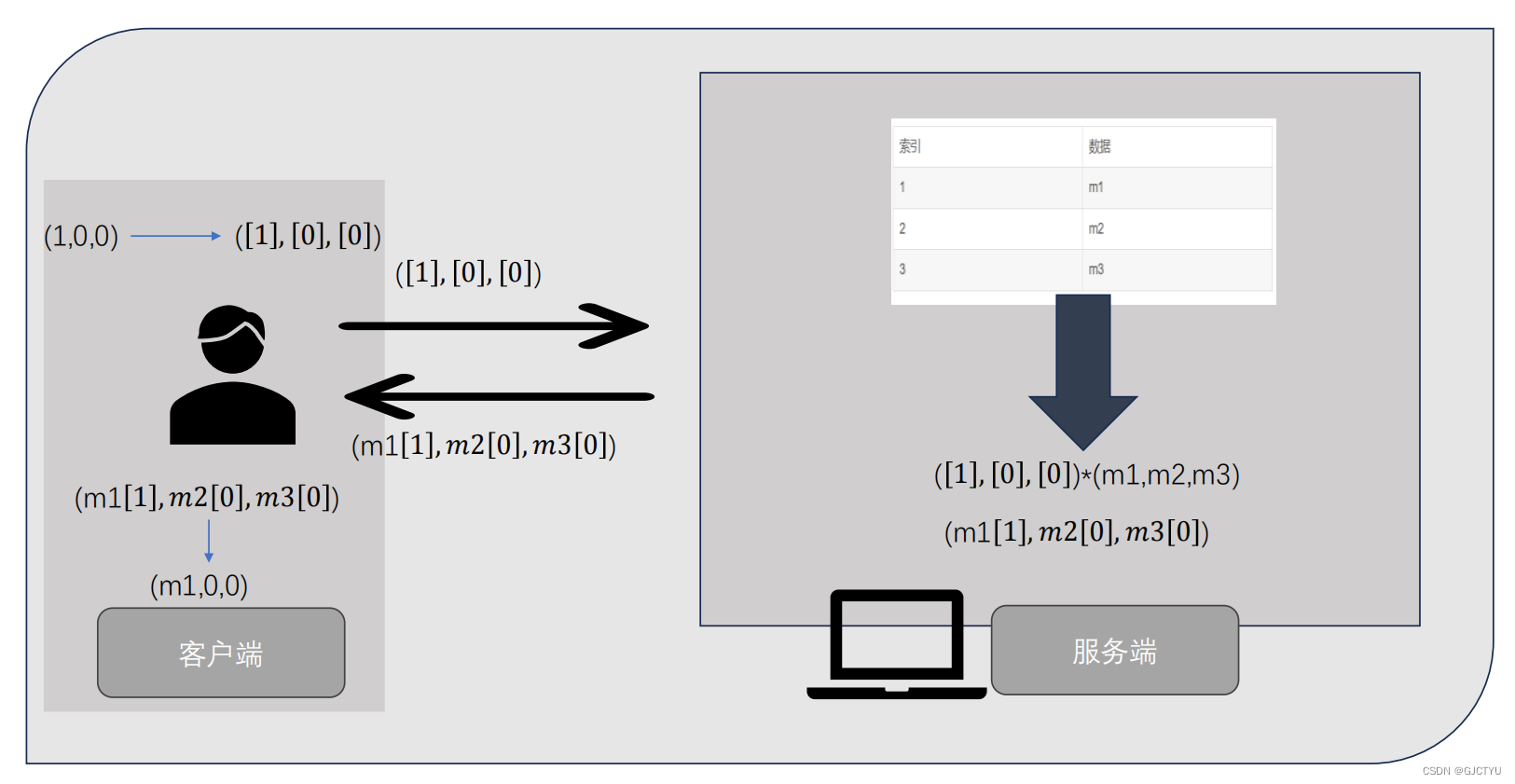

客户端想查询索引为1的数据，自己生成（1，0，0）每位加密后发送给服务端，服务端和数据向量做内积返回，客户端解密得到值

2.4基于同态加密的PIR实现

python简单复现

from phe import paillier
import numpy as np

# 用户端
def user_side(t, n):
    public_key, private_key = paillier.generate_paillier_keypair()

    # 创建向量
    vector = [public_key.encrypt(0) for _ in range(n)]
    vector[t] = public_key.encrypt(1)

    return vector, public_key, private_key

# 服务端
def server_side(vector, plaintext_data):
    encrypted_result = sum([vector[i] * plaintext_data[i] for i in range(len(plaintext_data))])
    return encrypted_result

# 用户端
def user_decrypt_result(encrypted_result, private_key):
    decrypted_result = private_key.decrypt(encrypted_result)
    return decrypted_result

# 测试
n = 10  # 数据条数
t = 3   # 要检索的第t条数据

plaintext_data = np.random.randint(1, 100, size=n)  # 模拟n条明文数据集

vector, public_key, private_key = user_side(t, n)
encrypted_result = server_side(vector, plaintext_data)
decrypted_result = user_decrypt_result(encrypted_result, private_key)

print("明文数据集:", plaintext_data)
print("解密后的结果:", decrypted_result)

谢谢阅读，创造不易，求点赞