一、链表的概念及结构
概念:链表是一种物理存储结构上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的 。
逻辑结构:想象出来的,为了便于理解。

物理结构:在内存中实际是如何存储的

实际中链表的结构非常多样,以下情况组合起来就有8种链表结构:
- 单向、双向
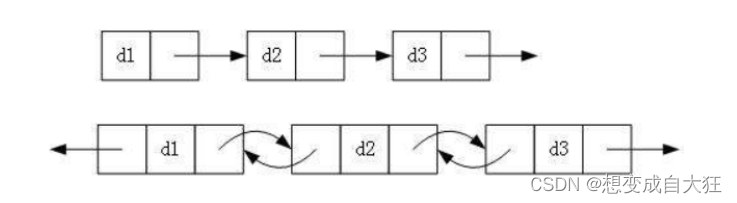
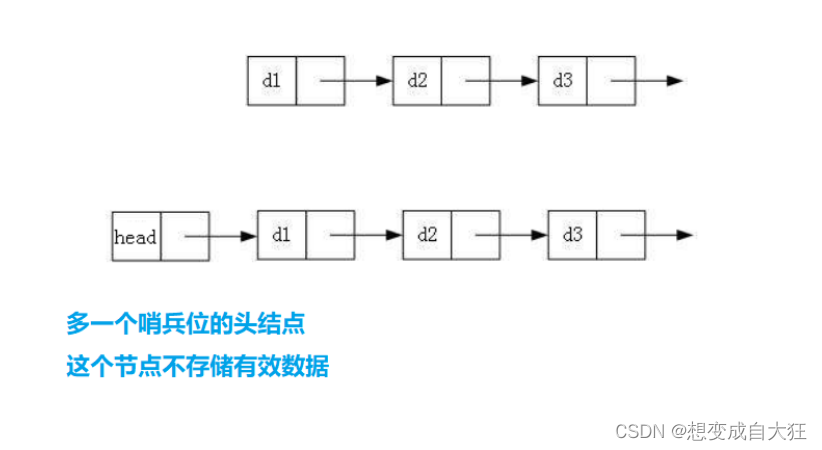
- 带头、不带头
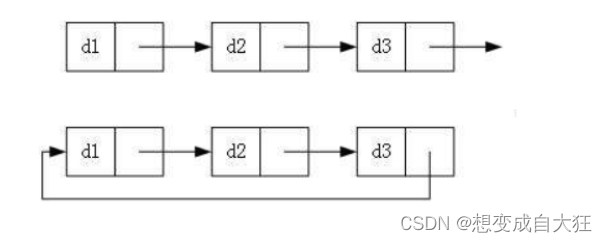
- 循环、非循环
虽然有这么多的链表的结构,但是我们实际中最常用还是两种结构:
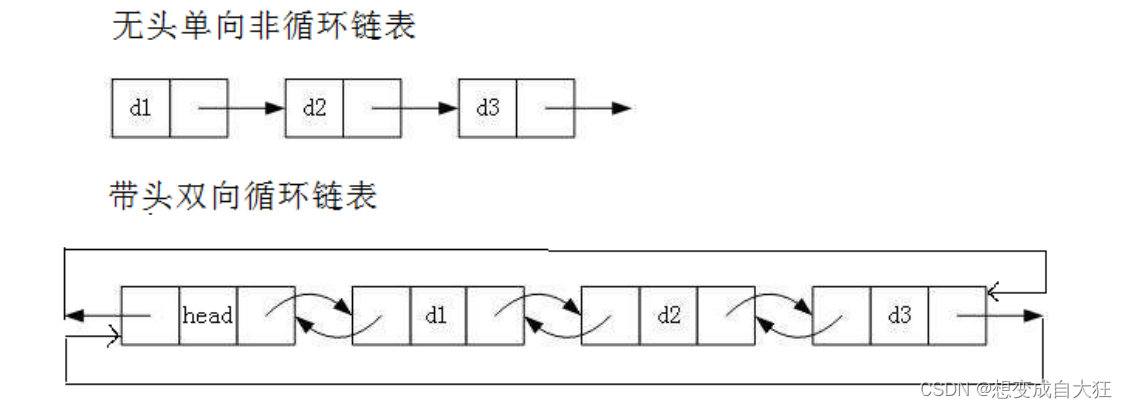
无头单向非循环链表:结构简单,一般不会单独用来存数据。实际中更多是作为其他数据结构的子结 构,如哈希桶、图的邻接表等等。另外这种结构在笔试面试中出现很多。
带头双向循环链表:结构最复杂,一般用在单独存储数据。实际中使用的链表数据结构,都是带头双向循环链表。另外这个结构虽然结构复杂,但是使用代码实现以后会发现结构会带来很多优势,实现反而简单了。
二、链表的实现
1、无头+单向+非循环链表增删查改实现
SList.h ---函数的声明
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int SLTDataType;
typedef struct SListNode {
SLTDataType data;
struct SlistNode* next;
}SLTNode;
void SListPrint(SLTNode* phead);
//链表后插入节点
void SListPushBack(SLTNode** pphead,SLTDataType x);
//链表前插入节点
void SListPushFront(SLTNode** pphead, SLTDataType x);
//链表后删除节点
void SListPopBack(SLTNode** pphead);
//链表前删除节点
void SListPopFront(SLTNode** pphead);
//查找
SLTNode* SListFind(SLTNode* phead, SLTDataType x);
//在pos位置之前插入一个节点
void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x);
//在pos位置之前插入一个节点
void SListInsertAfter(SLTNode* pos, SLTDataType x);
void SListErase(SLTNode** pphead, SLTNode* pos);
void SListEraseAfter(SLTNode* pphead, SLTNode* pos);
void SListDestory(SLTNode** pphead);
//void SListInsert(SLTNode**pphead, int pos, SLTDataType x);
SList.c ---函数的实现
#include "SList.h"
SLTNode* BuyListNode(SLTDataType x)
{
SLTNode* newnode = (SLTNode*)malloc(sizeof(SLTNode));
if (newnode == NULL)
{
printf("%s\n", "malloc fail");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
return newnode;
}
void SListPrint(SLTNode* phead)
{
assert(phead);
SLTNode* cur = phead;
while (cur != NULL)
{
printf("%d->", cur->data);
cur = cur->next;
}
printf("\n");
}
void SListPushBack(SLTNode** pphead, SLTDataType x)
{
assert(pphead);
SLTNode* newnode = BuyListNode(x);
if (*pphead == NULL)
{
*pphead = newnode;
}
else
{
//找到尾节点
SLTNode* tail = *pphead;
while (tail->next != NULL)
{
tail = tail->next;
}
tail->next = newnode;
}
}
void SListPushFront(SLTNode** pphead, SLTDataType x)
{
assert(pphead);
SLTNode* newnode = BuyListNode(x);
newnode->next = *pphead;
*pphead = newnode;
}
void SListPopBack(SLTNode** pphead)
{
assert(*pphead);
//只有一个节点
if ((*pphead)->next == NULL)
{
free(*pphead);
*pphead = NULL;
}
else
{
SLTNode* tail = *pphead;
SLTNode* prev = NULL;
while (tail->next!= NULL)
{
prev = tail;
tail = tail->next;
}
free(tail);
tail = NULL;
prev->next = NULL;
}
/*SLTNode* tail = *pphead;
while (tail->next->next)
{
tail = tail->next;
}
free(tail->next);
tail->next = NULL;*/
}
void SListPopFront(SLTNode** pphead)
{
assert(*pphead != NULL);
SLTNode* next = (*pphead)->next;
free(*pphead);
*pphead=next;
}
SLTNode* SListFind(SLTNode* phead, SLTDataType x)
{
assert(phead);
SLTNode* cur = phead;
while (cur != NULL)
{
if (cur->data == x)
return cur;
else
cur = cur->next;
}
return NULL;
}
//在pos位置之后去插入一个节点(更适合单链表,更简单) O(1)
void SListInsertAfter(SLTNode* pos, SLTDataType x)
{
assert(pos);
SLTNode* newnode = BuyListNode(x);
newnode->next=pos->next ;
pos->next = newnode;
}
//在pos位置之前去插入一个节点 O(n)
void SListInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)
{
assert(pphead);
SLTNode* newnode = BuyListNode(x);
if (*pphead == pos)
{
newnode->next = *pphead;
*pphead = newnode;
}
else
{
//找到pos的前一个位置
SLTNode* posPrev = *pphead;
while (posPrev->next != pos)
{
posPrev = posPrev->next;
}
posPrev->next = newnode;
newnode->next = pos;
}
}
void SListErase(SLTNode** pphead, SLTNode* pos)
{
assert(pphead);
if (*pphead == pos)
{
/* *pphead = pos->next;
free(pos);*/
SListPopFront(pphead);
}
else
{
SLTNode* prev = *pphead;
while (prev->next != pos)
{
prev = prev->next;
}
prev->next = pos->next;
free(pos);
}
}
void SListEraseAfter(SLTNode* pphead, SLTNode* pos)
{
assert(pos);
assert(pos->next);
SLTNode* next = pos->next;
pos->next = next->next;
free(next);
//next = NULL;
}
void SListDestory(SLTNode** pphead)
{
assert(pphead);
SLTNode* cur = pphead;
while (cur)
{
SLTNode* next = cur->next;
free(cur);
cur = next;
}
*pphead == NULL;
}
2、带头+双向+循环链表增删查改实现
DList.h ---函数的声明
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef int DLTDataType;
typedef struct DLTNode {
DLTDataType data;
struct DLTNode* prev;
struct DLTNode* next;
}DLTNode;
DLTNode* DListInit();
DLTNode* DListDestroy(DLTNode* phead);
DLTNode* BuyListNode(DLTDataType x);
void DListPrintf(DLTNode* phead);
void DListPushBack(DLTNode* phead,DLTDataType x);
void DListPopBack(DLTNode* phead);
void DListPushFront(DLTNode* phead, DLTDataType x);
void DListPopFront(DLTNode* phead);
DLTNode* DListFind(DLTNode* phead, DLTDataType x);
void DListInsert(DLTNode* pos, DLTDataType x);
void DListErase(DLTNode* pos);
DList.c ---函数的实现
#include "DList.h"
DLTNode* DListInit()
{
//哨兵位头节点
DLTNode* phead = (DLTNode * )malloc(sizeof(DLTNode));
if (phead ==NULL)
exit(-1);
phead->prev = phead;
phead->next = phead;
return phead;
}
DLTNode* BuyListNode(DLTDataType x)
{
DLTNode* newnode = (DLTNode*)malloc(sizeof(DLTNode));
if (newnode == NULL)
{
printf("%s\n", "内存分配不成功");
exit(-1);
}
newnode->data = x;
newnode->prev = NULL;
newnode->next = NULL;
return newnode;
}
void DListPrintf(DLTNode* phead)
{
assert(phead);
DLTNode* cur = phead->next;
while (cur!=phead)
{
printf("%d ", cur->data);
cur = cur->next;
}
printf("\n");
}
void DListPushBack(DLTNode* phead, DLTDataType x)
{
assert(phead);
/*DLTNode* tail=phead->prev;
DLTNode* newnode = BuyListNode(x);
tail->next = newnode;
newnode->prev =tail;
newnode->next = phead;
phead->prev = newnode;*/
DListInsert(phead, x);
}
void DListPopBack(DLTNode* phead)
{
assert(phead);
assert(phead->next != phead);
DLTNode* tail = phead->prev;
DLTNode* prevtail = tail->prev;
free(tail);
prevtail->next = phead;
phead->prev = prevtail;
}
void DListPushFront(DLTNode* phead, DLTDataType x)
{
assert(phead);
/*DLTNode* newnode = BuyListNode(x);
DLTNode* next = phead->next;
phead->next = newnode;
newnode->prev = phead;
newnode->next = next;
next->prev = newnode;*/
DListInsert(phead->next, x);
}
void DListPopFront(DLTNode* phead) {
assert(phead);
assert(phead->next != phead);
DLTNode* next = phead->next;
DLTNode* nextNext= next->next;
phead->next = nextNext;
nextNext->prev = phead;
free(next);
}
DLTNode* DListFind(DLTNode* phead, DLTDataType x)
{
assert(phead);
DLTNode* cur = phead->next;
while (cur != phead)
{
if (cur->data == x)
{
return cur;
}
else
{
cur = cur->next;
}
}
return NULL;
}
//pos位置之前插入
void DListInsert(DLTNode* pos, DLTDataType x)
{
assert(pos);
DLTNode* posPrev = pos->prev;
DLTNode* newnode = BuyListNode(x);
posPrev->next = newnode;
newnode->prev = posPrev;
newnode->next = pos;
pos->prev = newnode;
}
void DListErase(DLTNode* pos)
{
DLTNode* posPrev = pos->prev;
DLTNode* posNext = pos->next;
posPrev->next = posNext;
posNext->prev = posPrev;
free(pos);
}
DLTNode* DListDestroy(DLTNode* phead)
{
assert(phead);
DLTNode* cur = cur->next;
while (cur != phead)
{
DLTNode* next = cur->next;
free(cur);
cur = next;
}
free(phead);
phead = NULL;
return NULL;
}
三、顺序表和链表的优缺点
顺序表
优点:
1、支持随机访问。需要随机访问结构支持算法可以很好的适用。
2、cpu高速缓存命中率更高。
缺点:
1、头部中部插入删除时间效率低。O(n)
2、连续的物理空间,空间不够了以后需要增容。
a、增容有一定的程序消耗
b、为了避免频繁增容,一般我们都按倍数去增,用不完可能存在一定的空间浪费。
链表(双向带头循环链表)
优点:
1、任意位置插入删除效率高.O(1)
2、按需申请释放空间。
缺点:
1、不支持随机访问。(用下标访问)意味着:一些排序、二分查找等在这种结构上不适用。
2、链表储存一个值,同时需要存储链接指针,也有一定的消耗。
3、cpu高速缓存率更低。
四、链表常见的面试题
1. 删除链表中等于给定值 val 的所有节点
移除链表元素https://leetcode.cn/problems/remove-linked-list-elements/
给你一个链表的头节点
head
和一个整数
val
,请你删除链表中所有满足
Node.val == val
的节点,并返回 新的头节点 。
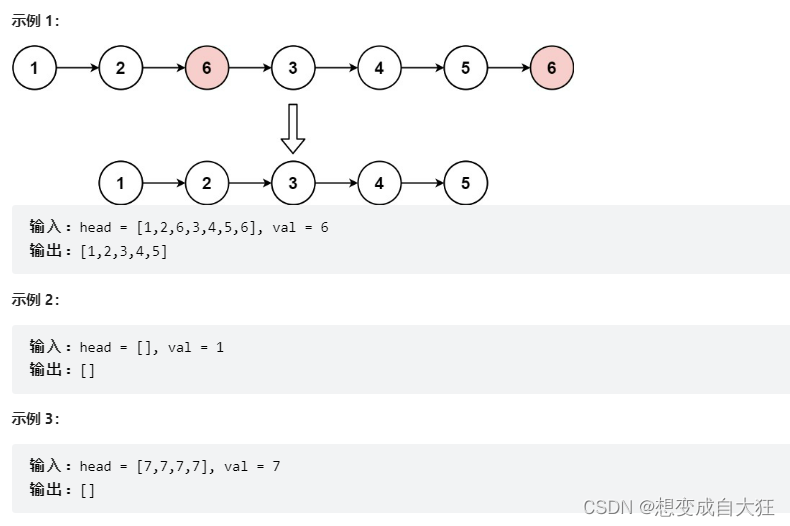
struct ListNode* removeElements(struct ListNode* head, int val){
Struct ListNode* cur=head;
Struct ListNode* prev=NULL;
while(cur!=NULL)
{
//1.头删
//2.中间删除
if(cur->val==val)
{
if(cur==head)
{
head=cur->next;
free(cur);
cur=head;
}
else{
prev=cur->next;
free(cur);
cur=prev->next;
}
}
else
{
//迭代往后走
prev=cur;
cur=cur->next;
}
}
}
2. 反转一个单链表。
反转链表https://leetcode.cn/problems/reverse-linked-list/
给你单链表的头节点
head
,请你反转链表,并返回反转后的链表
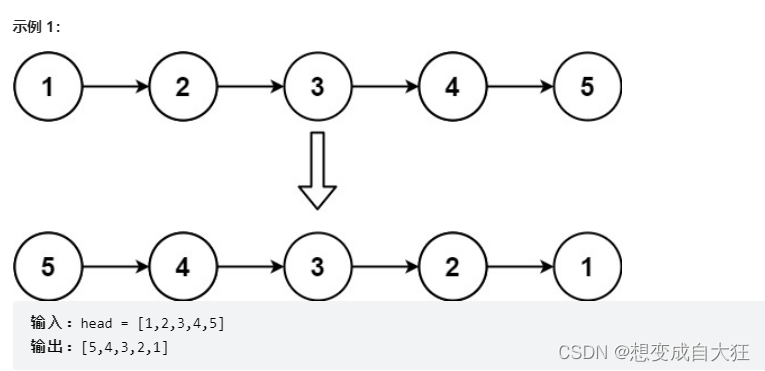
思路一:将链表直接翻转

struct ListNode* reverseList(struct ListNode* head){
if(head==NULL)
return NULL;
struct ListNode*n1=NULL;
struct ListNode*n2=head;
struct ListNode*n3=head->next;
while(n2)
{
//翻转
n2->next=n1;
//迭代往后走
n1=n2;
n2=n3;
if(n3)
n3=n3->next;
}
return n1;
}
反转链表思路二:创建一个新的头节点,头插。
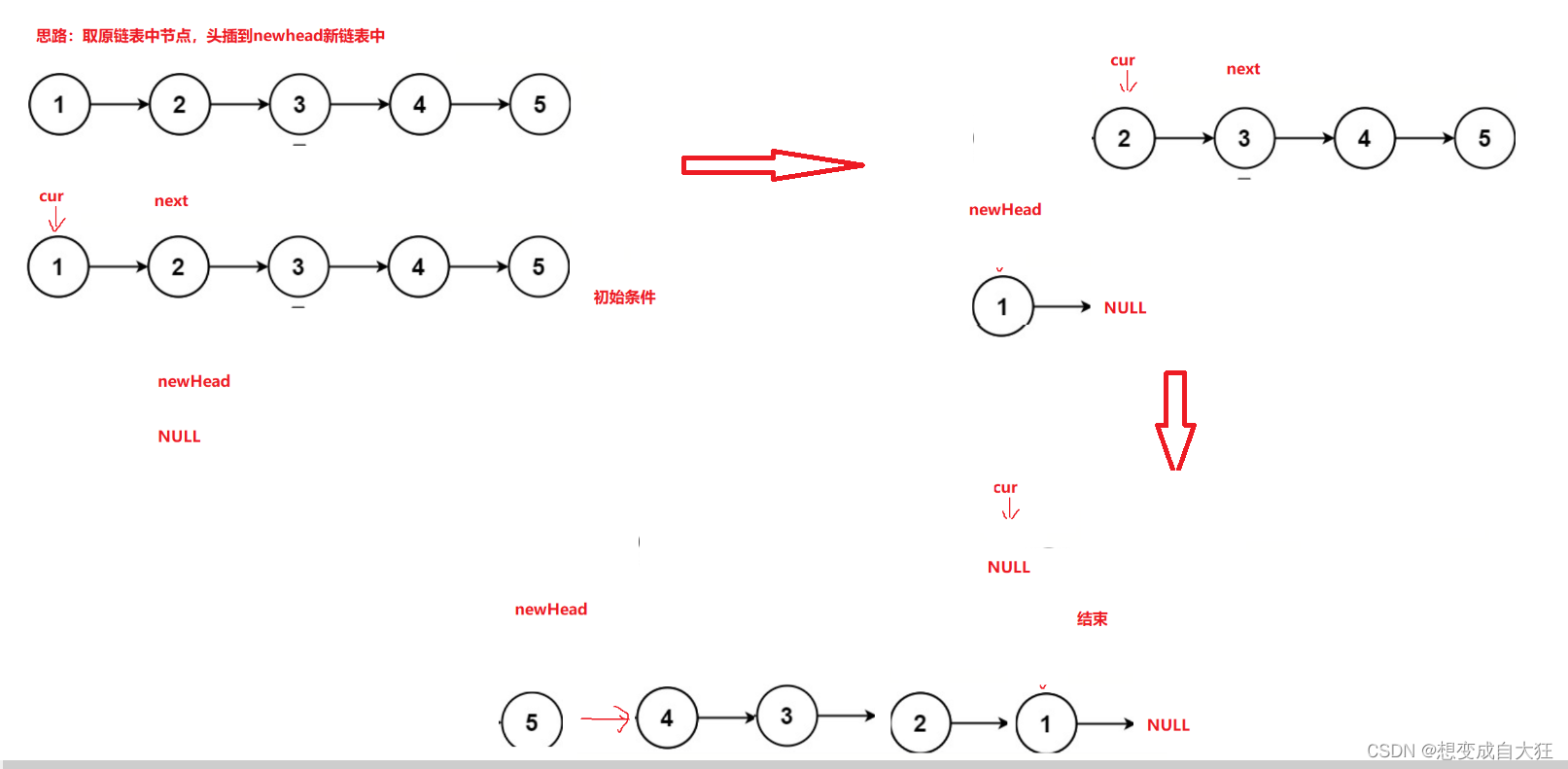
struct ListNode* reverseList(struct ListNode* head){
struct ListNode*newhead=NULL;
struct ListNode*cur=head;
while(cur)
{
struct ListNode*next=cur->next;
//头插
cur->next=newhead;
newhead=cur;
//迭代往后走
cur=next;
}
return newhead;
}
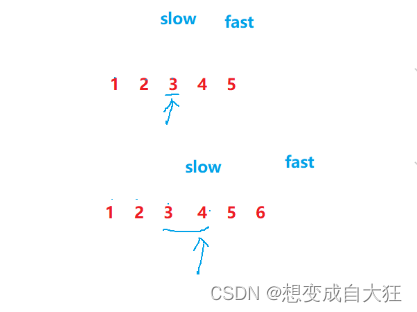
3. 给定一个带有头结点 head 的非空单链表,返回链表的中间结点。如果有两个中间结点,则返回第二个 中间结点。
思路:可以直接遍历一遍计算出链表的长度,再遍历一遍找到 长度/2 的位置,时间复杂度是O(n).
快慢指针法:定义一个快指针,一个慢指针,快指针走两步,慢指针走一步,当快指针走到最后一个节点(链表的元素是奇数个)或者走到空时(链表的元素是偶数个),慢指针走到的位置就是中间节点。
struct ListNode* middleNode(struct ListNode* head){
struct ListNode*fast,*slow;
fast=head;
slow=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
}
return slow;
}
4. 输入一个链表,输出该链表中倒数第k个结点。

思路:1.fast先走k步 2.slow和fast再一起走,fast==NULL时,slow就是倒数第k个节点
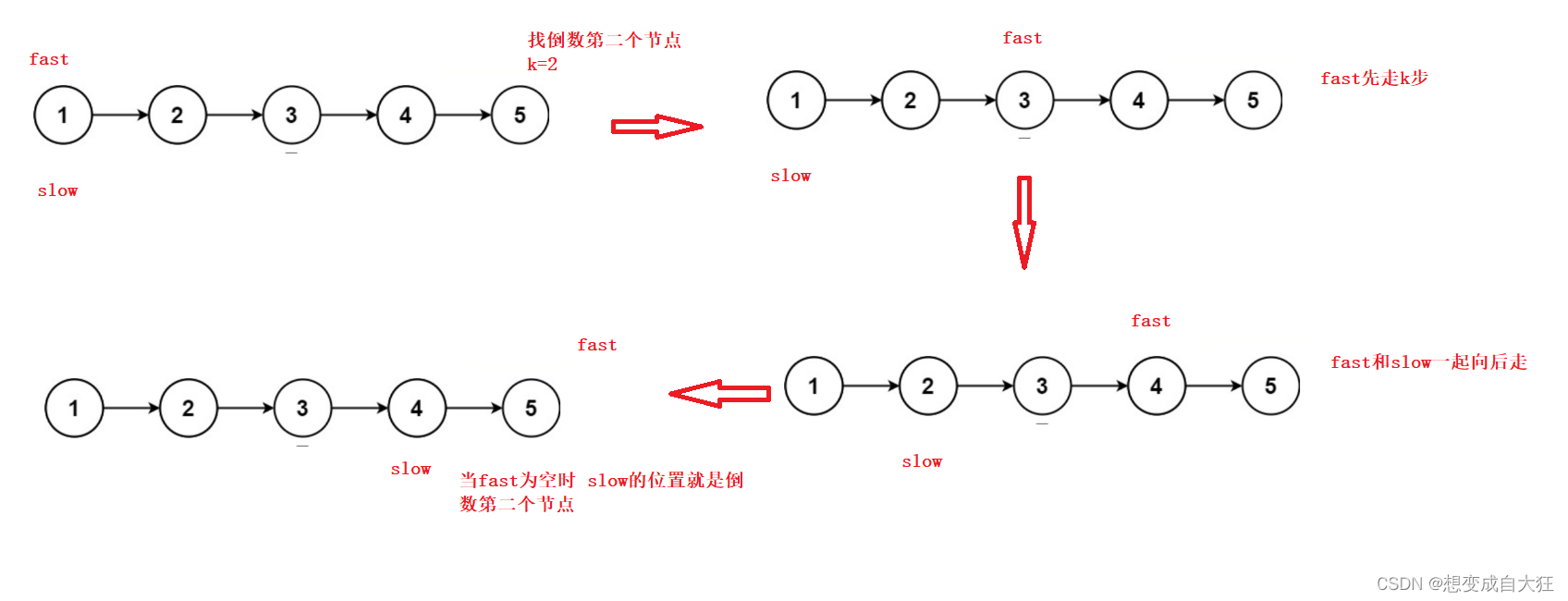
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k ) {
struct ListNode*fast,*slow;
fast=slow=pListHead;
while(k--)
{
//k大于链表的长度
if(fast==NULL)
return NULL;
fast=fast->next;
}
while(fast)
{
fast=fast->next;
slow=slow->next;
}
return slow;
}
5. 将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
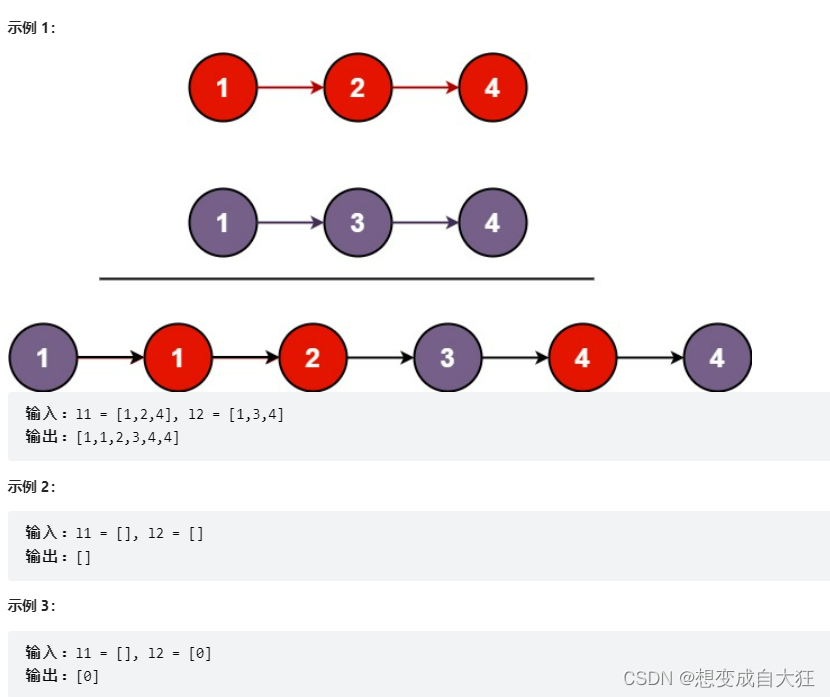
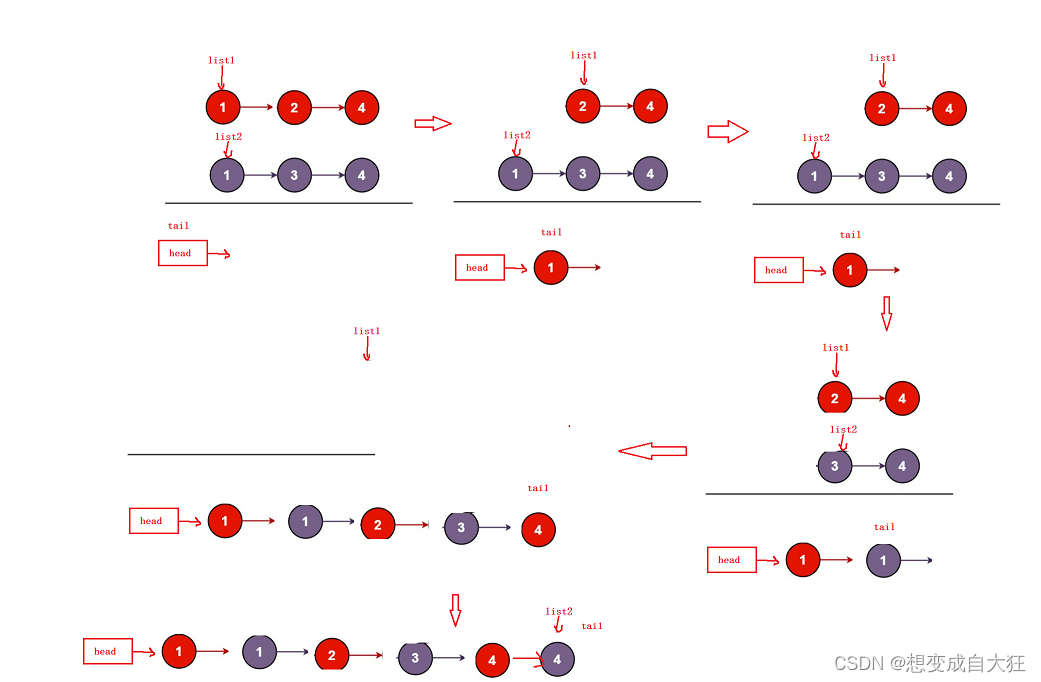
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2){
struct ListNode*head=NULL;
struct ListNode*tail=NULL;
//如果一个链表为空,返回另一个链表
if(list2==NULL)
return list1;
if(list1==NULL)
return list2;
/*//取两个链表第一个节点中较小的那一个作为头节点
if(list1->val<list2->val)
{
head=tail=list1;
list1=list1->next;
}
else
{
head=tail=list2;
list2=list2->next;
}*/
//哨兵位的头节点
head=tail=(struct ListNode*)malloc(sizeof(struct ListNode));
while(list1&&list2)
{
if(list1->val<list2->val)
{
tail->next=list1;
tail=list1;
list1=list1->next;
}
else
{
tail->next=list2;
tail=list2;
list2=list2->next;
}
}
if(list1)
{
tail->next=list1;
}
if(list2)
{
tail->next=list2;
}
struct ListNode* list = head->next;
return list;
}
6. 现有一链表的头指针 ListNode* pHead,给一定值x,编写一段代码将所有小于x的结点排在其余结点之前,且不能改变原来的数据顺序,返回重新排列后的链表的头指针。
ListNode* partition(ListNode* pHead, int x) {
struct ListNode *lessHead,*greaterHead,*lessTail,*greaterTail;
//开一个哨兵位的头节点,方便尾插
lessHead=lessTail=(struct ListNode*)malloc(sizeof(struct ListNode));
lessTail->next=NULL;
greaterHead=greaterTail=(struct ListNode*)malloc(sizeof(struct ListNode));
greaterTail->next=NULL;
struct ListNode*cur= pHead;
while(cur)
{
if(cur->val<x)
{
lessTail->next=cur;
lessTail=cur;
}
else{
greaterTail->next=cur;
greaterTail=cur;
}
cur=cur->next;
}
lessTail->next=greaterHead->next;
greaterTail->next=NULL;//如果不将偏大的链表置为空,可能会形成环
struct ListNode*listHead=lessHead->next;
free(lessHead);
free(greaterHead);
return listHead;
}
7. 链表的回文结构。

思路:1.找到链表的中间节点 2.将链表的后半部分逆置 3.将链表的前半部分和逆置后的后半部分链表进行比较
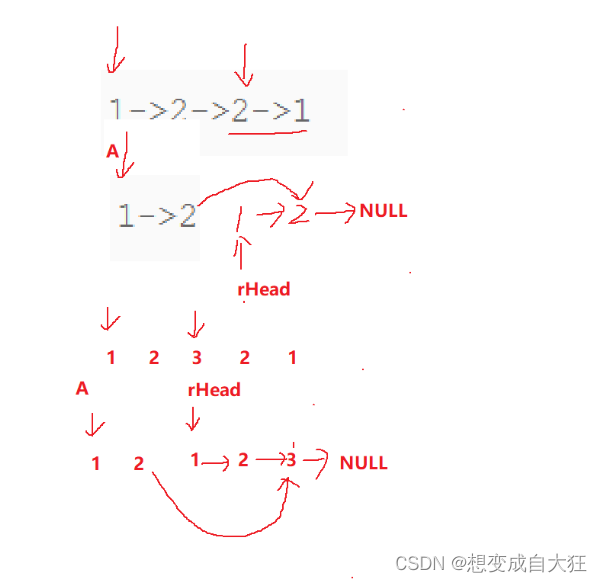
//找到中间节点
struct ListNode* middleNode(struct ListNode* head){
struct ListNode*fast,*slow;
fast=head;
slow=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
}
return slow;
}
//逆置
struct ListNode* reverseList(struct ListNode* head){
struct ListNode*newhead=NULL;
struct ListNode*cur=head;
while(cur)
{
struct ListNode*next=cur->next;
//头插
cur->next=newhead;
newhead=cur;
//迭代往后走
cur=next;
}
return newhead;
}
bool chkPalindrome(ListNode* A) {
struct ListNode*mid=middleNode(A);
struct ListNode*RHead=reverseList(mid);
struct ListNode*curA=A;
struct ListNode*curR=RHead;
while(curA&&curR)
{
if(curA->val!=curR->val)
{
return false;
}
else{
curA=curA->next;
curR=curR->next;
}
}
return true;
}
8. 输入两个链表,找出它们的第一个公共结点。
思路一:
暴力求解---穷举(O(n^2))
依此取A链表中的每个节点跟B链表中的所有节点比较,如果有地址相同的节点,就是相交,第一个相交的节点就是第一个公共节点。
思路二:(要求时间复杂度优化到O(n))
1.尾节点相同就是相交(单链表相交尾节点一定相同,因为一个节点只能存一个指针,呈横着的“Y”),否则就是不相交。
2.求交点:长的链表从头先走长度差步,再同时走,第一个相同的节点就是交点。
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
struct ListNode *tailA=headA;
struct ListNode *tailB=headB;
int lenA=1;
while(tailA->next)
{
++lenA;
tailA=tailA->next;
}
int lenB=1;
while(tailB->next)
{
++lenB;
tailB=tailB->next;
}
//不相交
if(tailA!=tailB)
return NULL;
//长的链表先走差距步,再同时走找交点
int gap=abs(lenA-lenB);//abs--求绝对值
struct ListNode *longList=headA;
struct ListNode *shortList=headB;
if(lenA<lenB)
{
longList=headB;
shortList=headA;
}
while(gap--)
{
longList=longList->next;
}
while(longList!=shortList)
{
longList=longList->next;
shortList=shortList->next;
}
return longList;
}
9. 给定一个链表,判断链表中是否有环。
思路:
快慢指针法:slow和fast指向链表的开始,slow一次走一步,fast一次走两步,如果不带环,fast就会走到空,如果带环,fast就会再环里面追上slow。

bool hasCycle(struct ListNode *head) {
struct ListNode *fast=head,*slow=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(fast==slow)
return true;
}
return false;
}
问题:
1.当fast一次走两步,slow一次走一步时,为什么slow和fast一定会在环中相遇吗?如果是,请证明。
slow和fast,一定是fast先进环,这时slow走了入环前距离的一半,随着slow进环,fast已经在环里面走了一段,走的距离跟环的大小有关。假设slow进环的时候,slow和fast的距离是N,fast开始追slow,slow每往前走一步,fast往前走两步,每追一次,判断是否相遇。追及过程中,fast和slow的距离变化:N,N-1,N-2,N-3....1,0。每追一次,fast和slow的距离就减少1,当fast和slow的距离为0是,就是相遇的点。
2.能不能fast走一次走n步(n>2),当fast一次走n步时,slow和fast是否能够相遇?
假设slow一次走一步,fast一次走三步,slow进环以后,fast跟slow之间的距离为N,fast开始追slow,他们的距离变化:当N时偶数时:N,N-2,N-4,N-6....2,0,这时fast可以追上slow;当N时奇数时:N,N-2,N-4,N-6....1,-1,这时fast追不上slow。如果N是奇数,距离变成-1意味着fast和slow的距离变成C-1(C是环的长度),如果C-1是奇数,就永远追不上了,如果C-1是偶数,就可以追上。
10. 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 NULL
环形链表 IIhttps://leetcode.cn/problems/linked-list-cycle-ii/
结论:一个指针从相遇点开始走,一个指针从链表头开始走,他们会在环的入口点相遇。
证明:

struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode *fast=head,*slow=head;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(fast==slow)
{
//相遇
struct ListNode * meetnode=slow;
while(meetnode!=head)
{
head=head->next;
meetnode=meetnode->next;
}
return meetnode;
}
}
return NULL;
}
11. 给定一个链表,每个节点包含一个额外增加的随机指针,该指针可以指向链表中的任何节点或空节点。 要求返回这个链表的深度拷贝。
思路:
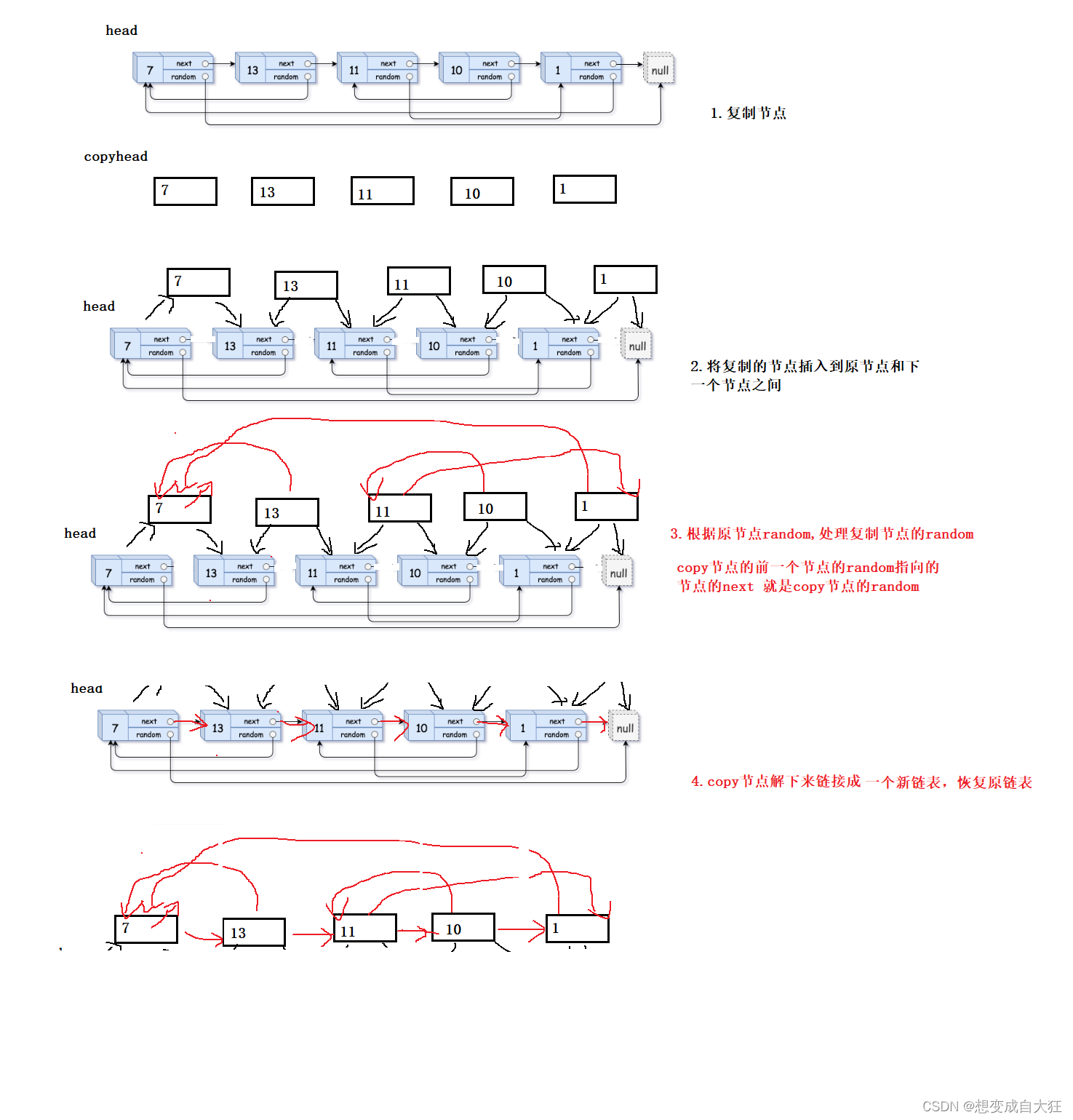
struct Node* copyRandomList(struct Node* head) {
//拷贝节点插入原节点的后面
struct Node*cur=head;
while(cur)
{
struct Node* copy=(struct Node*)malloc(sizeof(struct Node));
copy->val=cur->val;
//插入copy节点
copy->next=cur->next;
cur->next=copy;
cur=copy->next;
}
//根据原节点,处理copy节点的random
cur=head;
while(cur)
{
struct Node*copy=cur->next;
if(cur->random==NULL)
{
copy->random=NULL;
}
else
{
copy->random=cur->random->next;
}
cur=copy->next;
}
//将copy节点解下来链接成新链表,恢复原链表
struct Node* copyHead=NULL, *copyTail=NULL;
cur=head;
while(cur)
{
struct Node*copy=cur->next;
struct Node*next=copy->next;
if(copyTail==NULL)
{
copyHead=copyTail=copy;
}
else
{
copyTail->next=copy;
copyTail=copy;
}
cur->next=next;
cur=next;
}
return copyHead;
}
做数据结构的题一定要多画图,这样逻辑才会更清晰。
版权归原作者 想变成自大狂 所有, 如有侵权,请联系我们删除。