在 ShuffleNet v2 中提出了轻量化网络的 4 大设计准则:
- 输入输出通道相同时,MAC 最小
- FLOPs 相同时,分组数过大的分组卷积会增加 MAC
- 碎片化操作 (多分支结构) 对并行加速不友好
- 逐元素操作带来的内存和耗时不可忽略
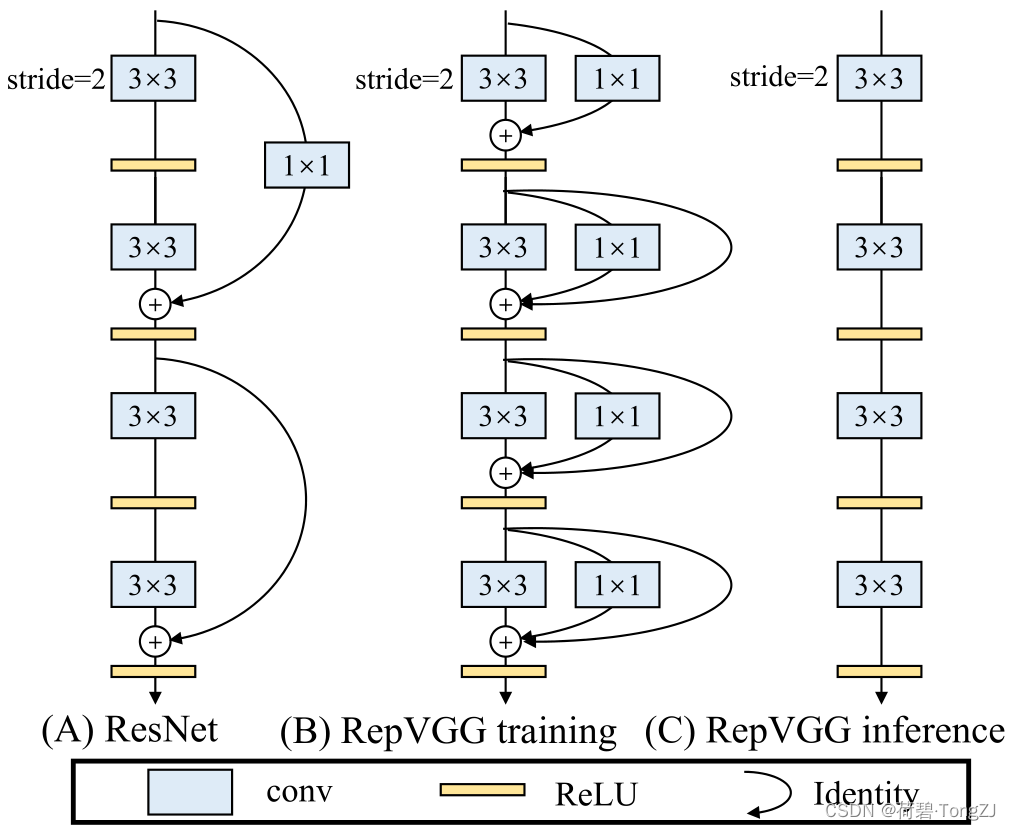
近年来,卷积神经网络的结构已经变得越来越复杂;得益于多分支结构良好的收敛能力,多分支结构越来越流行
但是,使用多分支结构的时候,一方面无法有效地利用并行加速,另一方面增加了 MAC
为了使简单结构也能达到与多分支结构相当的精度,在训练 RepVGG 时使用多分支结构 (3×3 卷积 + 1×1 卷积 + 恒等映射),以借助其良好的收敛能力;在推理、部署时利用重参数化技术将多分支结构转化为单路结构,以借助简单结构极致的速度
重参数化
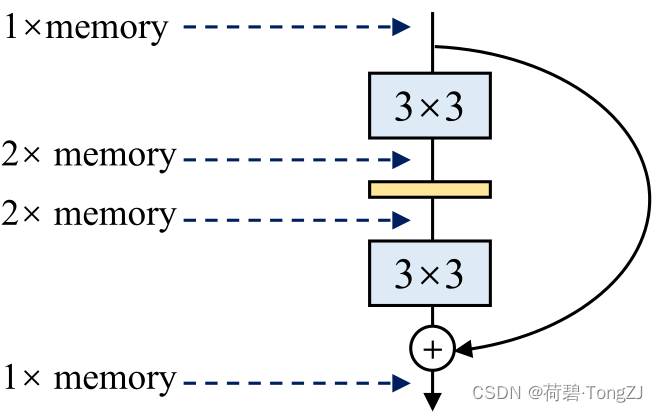
训练所使用的多分支结构中,每一个分支中均有一个 BN 层
BN 层有四个运算时使用的参数:mean、var、weight、bias,对输入 x 执行以下变换:
转化为 的形式时:
import torch
from torch import nn
class BatchNorm(nn.BatchNorm2d):
def unpack(self):
mean, weight, bias = self.running_mean, self.weight, self.bias
std = (self.running_var + self.eps).sqrt()
eq_weight = weight / std
eq_bias = bias - weight * mean / std
return eq_weight, eq_bias
bn = BatchNorm(8).eval()
# 初始化随机参数
bn.running_mean.data, bn.running_var.data, bn.weight.data, bn.bias.data = torch.rand([4, 8])
image = torch.rand([1, 8, 1, 1])
print(bn(image).view(-1))
# 将 BN 的参数转化为 w, b 形式
weight, bias = bn.unpack()
print(image.view(-1) * weight + bias)
因为 BN 层会拟合每一个通道的偏置,所以将卷积层和 BN 层连接在一起使用时,卷积层不使用偏置,其运算可以表示为:
可见,卷积层和 BN 层可以等价于一个带偏置的卷积层
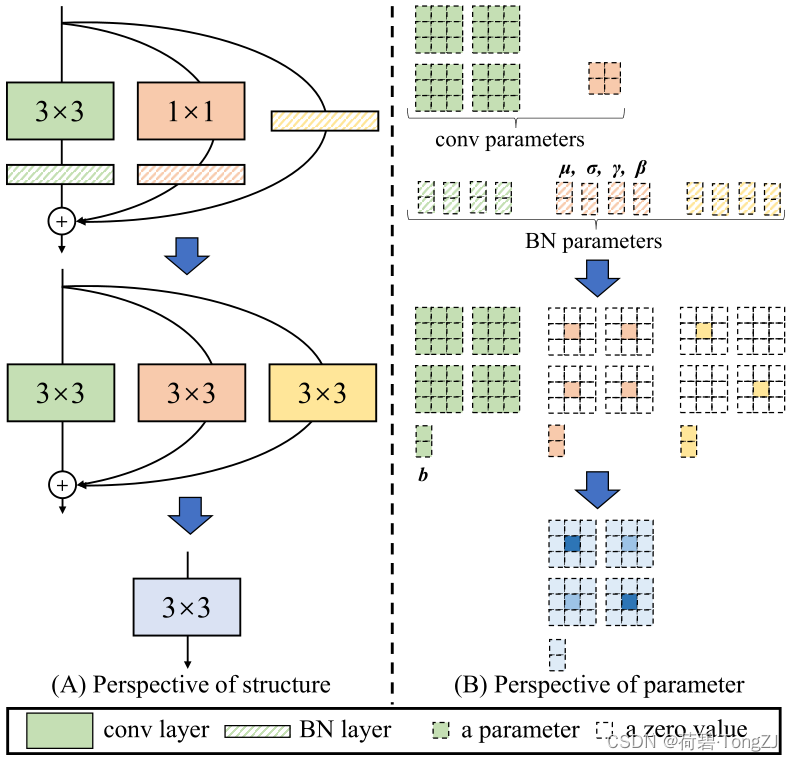
而恒等映射亦可等价于 1×1 卷积:
- 对于 nn.Conv2d(c1, c2, kernel_size=1),其参数的 shape 为 [c2, c1, 1, 1] —— 可看作 [c2, c1] 的线性层,以执行各个像素点的通道变换 (参考:PyTorch 二维多通道卷积运算方式)
- 当 c1 = c2、且这个线性层为单位阵时,等价于恒等映射
1×1 卷积又可通过填充 0 表示成 3×3 卷积,所以该多分支结构的计算可表示为:
从而可以等价成一个新的 3×3 卷积 (该结论亦可推广到分组卷积、5×5 卷积)
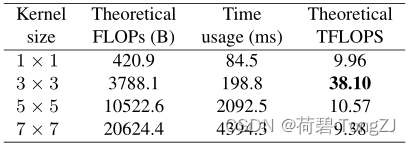
在 NVIDIA 1080Ti 上进行速度测试,以 [32, 2048, 56, 56] 的图像输入卷积核得到同通道同尺寸的输出,3×3 卷积每秒浮点运算量最多
结构复现
参考代码:https://github.com/DingXiaoH/RepVGG
我对论文中的源代码进行了重构,目的是增强其可读性、易用性 (为了可移植进 YOLO 项目,去除了 L2 范数的计算)
同时,我也将重参数化的函数写入类的静态方法,支持集成模型的重参数化
from collections import OrderedDict
import torch
import torch.nn.functional as F
from torch import nn
class BatchNorm(nn.BatchNorm2d):
def unpack(self):
mean, weight, bias = self.running_mean, self.weight, self.bias
std = (self.running_var + self.eps).sqrt()
eq_weight = weight / std
eq_bias = bias - weight * mean / std
return eq_weight, eq_bias
class RepVGGBlock(nn.Module):
def __init__(self, c1, c2, k=3, s=1, g=1, deploy=False):
super(RepVGGBlock, self).__init__()
self.deploy = deploy
# 校对卷积核的尺寸
assert k & 1, 'The convolution kernel size must be odd'
# 主分支卷积参数
self.conv_main_config = dict(
in_channels=c1, out_channels=c2, kernel_size=k,
stride=s, padding=k // 2, groups=g
)
if deploy:
self.conv_main = nn.Conv2d(**self.conv_main_config, bias=True)
else:
# 主分支
self.conv_main = nn.Sequential(OrderedDict(
conv=nn.Conv2d(**self.conv_main_config, bias=False),
bn=BatchNorm(c2)
))
# 1×1 卷积分支
self.conv_1x1 = nn.Sequential(OrderedDict(
conv=nn.Conv2d(c1, c2, 1, s, padding=0, groups=g, bias=False),
bn=BatchNorm(c2)
)) if k != 1 else None
# 恒等映射分支
self.identity = BatchNorm(c2) if c1 == c2 and s == 1 else None
def forward(self, x, act=F.silu):
y = self.conv_main(x)
if self.conv_1x1:
y += self.conv_1x1(x)
if self.identity:
y += self.identity(x)
# 使用激活函数
y = act(y) if act else y
return y
@staticmethod
def merge(model: nn.Module):
# 查询模型的所有子模型, 对 RepVGGBlock 进行合并
for m in model.modules():
if isinstance(m, RepVGGBlock) and not m.deploy:
# 主分支的信息
kernel = m.conv_main.conv.weight
(c2, c1_per_group, k, _), g = kernel.shape, m.conv_main.conv.groups
center_pos = k // 2
# 转换主分支
bn_weight, bn_bias = m.conv_main.bn.unpack()
kernel_weight, kernel_bias = kernel * bn_weight.view(-1, 1, 1, 1), bn_bias
# 转换 1×1 卷积分支
if m.conv_1x1:
kernel_1x1 = m.conv_1x1.conv.weight[..., 0, 0]
bn_weight, bn_bias = m.conv_1x1.bn.unpack()
kernel_weight[..., center_pos, center_pos] += kernel_1x1 * bn_weight.view(-1, 1)
kernel_bias += bn_bias
# 转换恒等映射分支
if m.identity:
kernel_id = torch.cat([torch.eye(c1_per_group)] * g, dim=0).to(kernel.device)
bn_weight, bn_bias = m.identity.unpack()
kernel_weight[..., center_pos, center_pos] += kernel_id * bn_weight.view(-1, 1)
kernel_bias += bn_bias
# 声明合并后的卷积核
m.conv_main = nn.Conv2d(**m.conv_main_config, bias=True)
m.conv_main.weight.data, m.conv_main.bias.data = kernel_weight, kernel_bias
# 删除被合并的分支
m.deploy = True
delattr(m, 'conv_1x1')
delattr(m, 'identity')
m.conv_1x1, m.identity = None, None
然后设计一个集成模型进行验证:
- merge 函数是否改变了网络结构
- 重参数化前后,模型的运算结果是否一致
- 重参数化后,模型的推理速度是否有所提升
if __name__ == '__main__':
class RepVGG(nn.Module):
def __init__(self, num_blocks, num_classes=1000, width_multiplier=None, deploy=False):
super(RepVGG, self).__init__()
assert len(width_multiplier) == 4
self.deploy = deploy
# 输入通道数
self.in_planes = min(64, int(64 * width_multiplier[0]))
self.stage0 = RepVGGBlock(3, self.in_planes, k=3, s=2, deploy=self.deploy)
# 主干部分分为四部分, 每一部分使用多个 RepVGGBlock 级联
self.stage1 = self._make_stage(int(64 * width_multiplier[0]), num_blocks[0], stride=2)
self.stage2 = self._make_stage(int(128 * width_multiplier[1]), num_blocks[1], stride=2)
self.stage3 = self._make_stage(int(256 * width_multiplier[2]), num_blocks[2], stride=2)
self.stage4 = self._make_stage(int(512 * width_multiplier[3]), num_blocks[3], stride=2)
self.gap = nn.AdaptiveAvgPool2d(output_size=1)
self.linear = nn.Linear(int(512 * width_multiplier[3]), num_classes)
def _make_stage(self, planes, num_blocks, stride):
strides = [stride] + [1] * (num_blocks - 1)
blocks = []
for stride in strides:
blocks.append(RepVGGBlock(self.in_planes, planes, k=3, s=stride, deploy=self.deploy))
self.in_planes = planes
return nn.Sequential(*blocks)
def forward(self, x):
out = self.stage0(x)
out = self.stage1(out)
out = self.stage2(out)
out = self.stage3(out)
out = self.stage4(out)
out = self.gap(out)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
vgg = RepVGG(num_blocks=[1, 1, 1, 1], num_classes=20,
width_multiplier=[1, 1, 1, 1]).eval()
print(vgg)
# 为 BatchNorm 初始化随机参数
for m in vgg.modules():
if isinstance(m, BatchNorm):
m.running_mean.data, m.running_var.data, \
m.weight.data, m.bias.data = torch.rand([4, m.num_features])
image = torch.rand([1, 3, 224, 224])
class Timer:
prefix = 'Cost: '
def __init__(self, fun, *args, **kwargs):
import time
start = time.time()
fun(*args, **kwargs)
cost = (time.time() - start) * 1e3
print(self.prefix + f'{cost:.0f} ms')
# 使用训练结构的 VGG 进行测试
print(vgg(image))
Timer(vgg, image)
# 调用 RepVGGBlock 的静态方法, 合并 RepVGGBlock 的分支
RepVGGBlock.merge(vgg)
print(vgg)
# 使用推理结构的 VGG 进行测试
print(vgg(image))
Timer(vgg, image)
RepVGG(
(stage0): RepVGGBlock(
(conv_main): Sequential(
(conv): Conv2d(3, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn): BatchNorm(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(conv_1x1): Sequential(
(conv): Conv2d(3, 64, kernel_size=(1, 1), stride=(2, 2), bias=False)
(bn): BatchNorm(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(stage1): Sequential(
(0): RepVGGBlock(
(conv_main): Sequential(
(conv): Conv2d(64, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn): BatchNorm(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(conv_1x1): Sequential(
(conv): Conv2d(64, 64, kernel_size=(1, 1), stride=(2, 2), bias=False)
(bn): BatchNorm(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
)
(stage2): Sequential(
(0): RepVGGBlock(
(conv_main): Sequential(
(conv): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn): BatchNorm(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(conv_1x1): Sequential(
(conv): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
(bn): BatchNorm(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
)
(stage3): Sequential(
(0): RepVGGBlock(
(conv_main): Sequential(
(conv): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn): BatchNorm(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(conv_1x1): Sequential(
(conv): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
(bn): BatchNorm(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
)
(stage4): Sequential(
(0): RepVGGBlock(
(conv_main): Sequential(
(conv): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn): BatchNorm(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(conv_1x1): Sequential(
(conv): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
(bn): BatchNorm(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
)
(gap): AdaptiveAvgPool2d(output_size=1)
(linear): Linear(in_features=512, out_features=20, bias=True)
)
tensor([[-0.1108, 0.0824, 0.5547, -0.1671, 0.7442, -0.1164, -0.2825, 0.4088,
0.1239, -0.3792, 0.1152, -0.4021, 0.4034, 0.2350, 0.2601, -0.1197,
0.2462, -0.2451, 0.0439, -0.2507]], grad_fn=<AddmmBackward>)
Cost: 22 msRepVGG(
(stage0): RepVGGBlock(
(conv_main): Conv2d(3, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
)
(stage1): Sequential(
(0): RepVGGBlock(
(conv_main): Conv2d(64, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
)
)
(stage2): Sequential(
(0): RepVGGBlock(
(conv_main): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
)
)
(stage3): Sequential(
(0): RepVGGBlock(
(conv_main): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
)
)
(stage4): Sequential(
(0): RepVGGBlock(
(conv_main): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1))
)
)
(gap): AdaptiveAvgPool2d(output_size=1)
(linear): Linear(in_features=512, out_features=20, bias=True)
)
tensor([[-0.1108, 0.0824, 0.5547, -0.1671, 0.7442, -0.1164, -0.2825, 0.4088,
0.1239, -0.3792, 0.1152, -0.4021, 0.4034, 0.2350, 0.2601, -0.1197,
0.2462, -0.2451, 0.0439, -0.2507]], grad_fn=<AddmmBackward>)
Cost: 14 ms
版权归原作者 荷碧·TongZJ 所有, 如有侵权,请联系我们删除。