数据结构之跳表（含代码实现）

1.跳表的相关概念

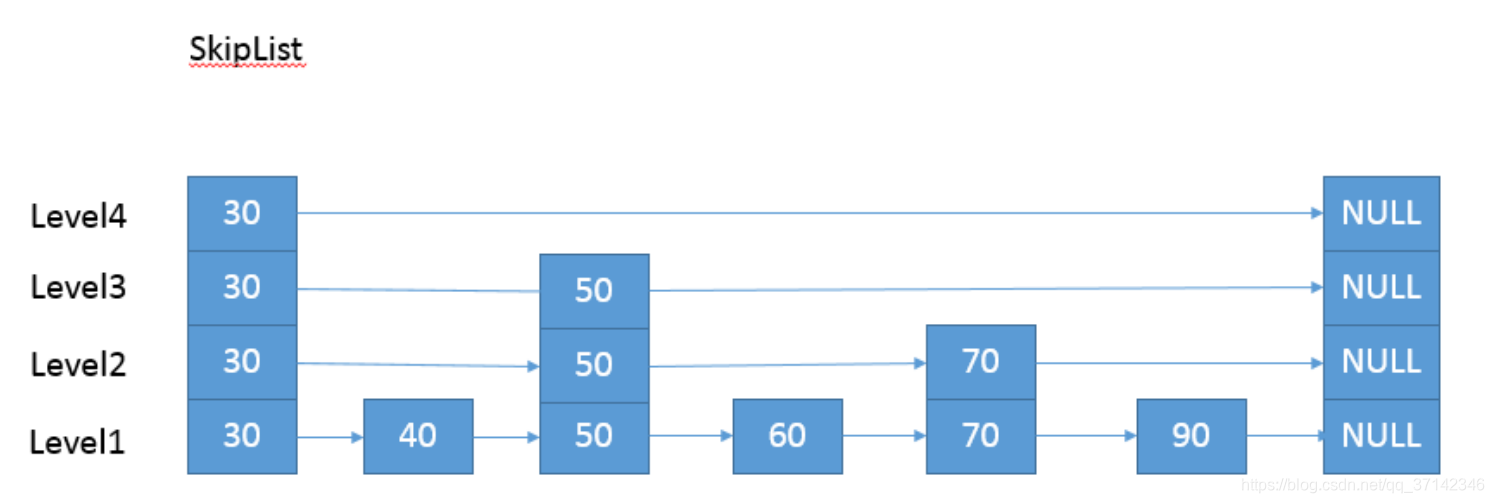
跳表全称为跳跃列表，它允许快速查询，插入和删除一个有序连续元素的数据链表。跳跃列表的平均查找和插入时间复杂度都是O(logn)。快速查询是通过维护一个多层次的链表，且每一层链表中的元素是前一层链表元素的子集（见右边的示意图）。一开始时，算法在最稀疏的层次进行搜索，直至需要查找的元素在该层两个相邻的元素中间。这时，算法将跳转到下一个层次，重复刚才的搜索，直到找到需要查找的元素为止。

下面这张图片就是跳表：

在学习跳表之前先来看一下以下内容：

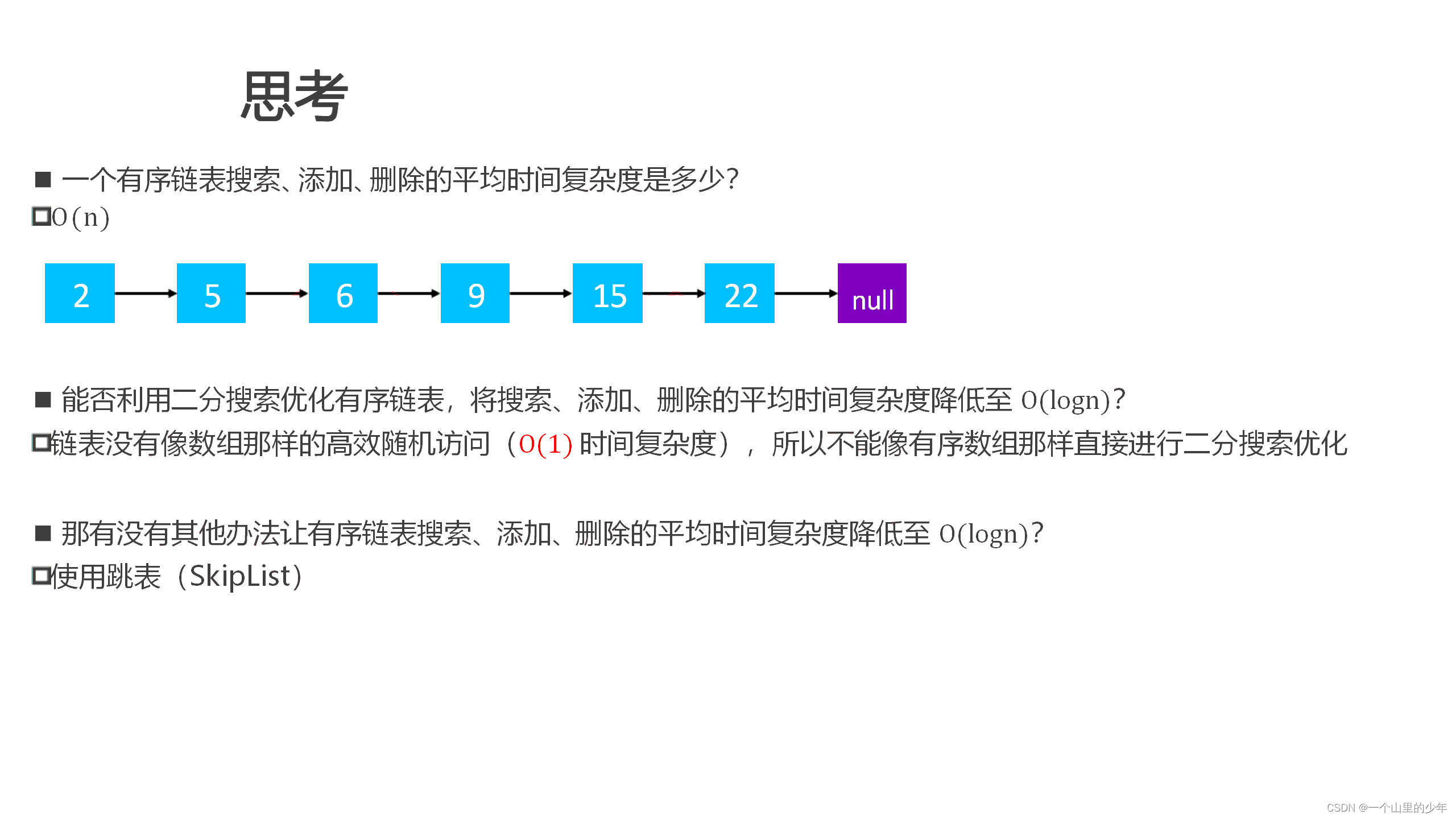
我们一前在有序数组中如何快速的查找一个数？答案是采用二分法。

首先根据数组的起始位置的下标和末尾位置的下标计算出中间位置的下标，在取出中间位置的值和要查找的值进行比较。

在本图中:

由于要查找的元素20，大于中间元素12，再次定位右到数组半部分的中间元素：

刚好查找到了20这个元素。

如果数组的长度为N，那么时间复杂度为O（log N)空间复杂度为O（1）。

如果是链表我们是否能够像数组那样进行二分查找？

由于链表不支持随机访问，无法像数组那样根据下标从而达到二分的效果。

那链表是否也能达到像数组那样查找一个数的时间复杂度为O（logN)?这时我们需要对链表进行升级.

如何进行升级呢？我们平时看一本书的时候的时候如何快速的查看某一章的内容呢？当然是我们首先看书的目录根据目录的提示翻到对应章的页码，然后直接翻到那一页。

那链表是否也能像书一样有目录或者说是索引？我们对链表改造一下

在原始链表中添加一个索引链表。这样做有什么好处呢？当我们想要定位到结点20，我们不需要在原始链表中一个一个结点访问，而是首先访问索引链表：

在索引链表找到结点20之后，我们顺着索引链表的结点向下，找到原始链表的结点20：

使用索引链表虽然能够让效率提高了一半，那有没有更好一点的方法进一步优化呢？

一本书中一般第几章中会写着第几节，这样能够大大的提高查找效率。如果我们将链表也设计成这样，效率不就提高了吗？

我们进一步对链表进行改进。

如图所示，我们基于原始链表的第1层索引，抽出了第2层更为稀疏的索引，结点数量是第1层索引的一半。

这样的多层索引可以进一步提升查询效率，假如仍然要查找结点20，让我们来演示一下过程：

首先，我们从最上层的索引开始查找，找到该层中仅小于结点20的前置索引结点12：

接下来，我们顺着结点12访问下一层索引，在该层中找到结点20：

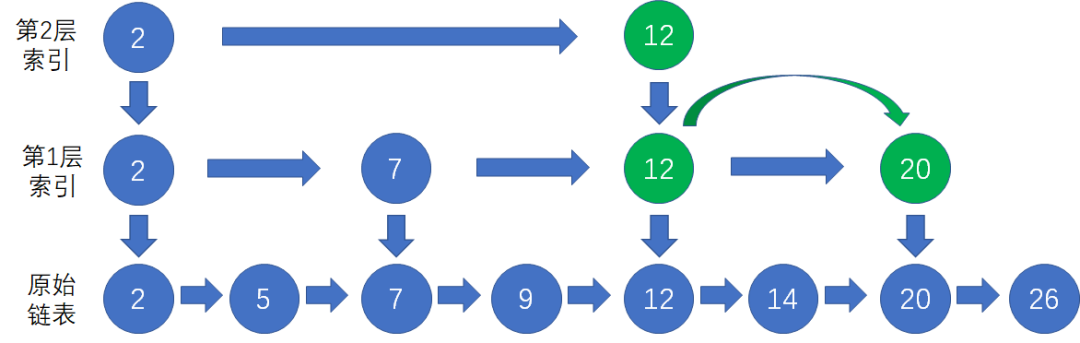
最后，我们顺着第1层索引的结点20向下，找到原始链表的结点20：

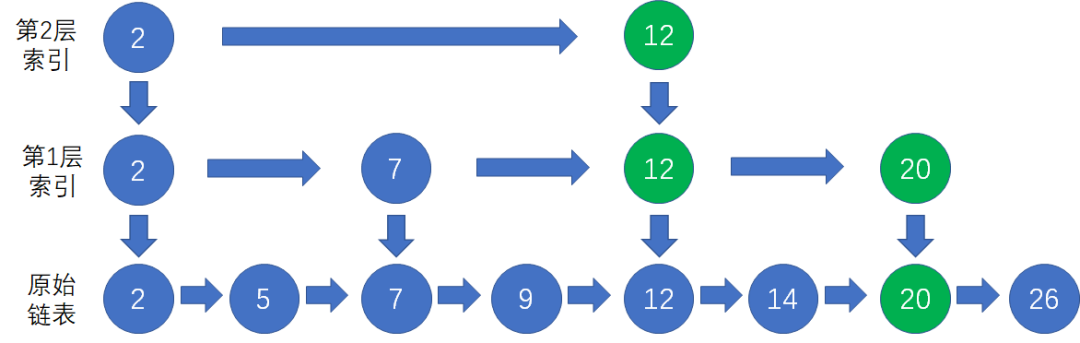
由于原始链表的结点数量较少，仅仅需要2层索引。如果链表的结点数量非常多，我们就可以抽出更多的索引层级，每一层索引的结点数量都是低层索引的一半。

这样就能极大的提高效率，使其时间复杂度直接优化到O（logN) 。

证明过程：

像这样对链表进行优化的结构就叫做跳表。

2.跳表节点的定义及其实现

我们首先来看跳表节点定义：

struct SkipListNode
{
    SkipListNode(const pair<K, V>& kv, bool flag = true)
        :_kv(kv)
        , _flag(flag)

    {}
    bool isKeyLess(const K& othoerKey) {//判断当前节点是否小于otherkey
        return  _flag || othoerKey > _kv.first;
    }
    bool isKeyEqual(const K& key) {
        return  key == _kv.first;//判断key和当前节点是否相等

    }
    vector<SkipListNode<K, V>*>nextNodes;//存储指针
    pair<K, V>_kv;//存储数据
    bool _flag;//标记是否为头节点
};

当然老铁也可以使用list来存储，本人习惯了vector.

一般跳表中会存这样一些变量：

private:
    const double PROBABILITY = 0.5;//0.5的概率
    Node* head;//头节点
    int _size;//个数
    int maxLevel;//最大的层数

2.1跳表的插入

假设我们要插入的结点是10，首先我们按照跳表查找结点的方法，找到待插入结点的前置结点（仅小于待插入结点，也就前驱节点），类似于链表的插入一样：

首先我们查找都是在最高层开始查找，找到前驱节点并将新的节点进行插入。

这样是不是插入工作就完成了呢？并不是。随着原始链表的新结点越来越多，索引会渐渐变得不够用了，因此索引结点也需要相应作出调整。

如何调整索引呢？我们让新插入的结点随机“晋升”，也就是成为索引结点。新结点晋升成功的几率是50%。

假设第一次随机的结果是晋升成功，那么我们把结点10作为索引结点，插入到第1层索引的对应位置，并且向下指向原始链表的结点10：

但是晋升的层数也有可能超过头节点的层数，此时我们需要将头节点加一层.

对应代码：

void Insert(const pair<K, V>& kv) {

        Node* less = mostRightLessNodeInTree(kv.first);//找到前驱节点
        Node* Find = less->nextNodes[0];//如果已经存在那么下一个就是要插入的这个值
        if (Find && Find->isKeyEqual(kv.first)) {//先判断是否已经存在
            return;
        }
        else {//不存在
            _size++;//将个数++
            int newNodelevel = 0;//记录该节点会有几层
            
            int seed = time(0);
            static default_random_engine tmp(seed);//随机数
            
            while (tmp()%100/100.0000<PROBABILITY){//0.5的概率小于0.5就++直到大于0.5
                newNodelevel++;
            }
    

            while (newNodelevel > maxLevel) {
                //如果超过了头节点中的最大层数那么将头节点的层数增加到当前节点的层数
                head->nextNodes.push_back(nullptr);//插入nullptr
                maxLevel++;
            }
            Node* newnode = new Node(kv, false);//创建新节点
            for (int i = 0; i <= newNodelevel; i++) {
                newnode->nextNodes.push_back(nullptr);//一开始每一层的指针指向空
            }
            int level = maxLevel;//从最高的那一层开始
            Node* pre = head;
            while (level >= 0) {//直到最底层

                pre = mostRightLessNodeLevel(kv.first, pre, level);//找到前区节点
                if (level <= newNodelevel) {//如果层数比当前节点的层数要多不用指向我
                    //插入
                    newnode->nextNodes[level] = pre->nextNodes[level];
                    pre->nextNodes[level] = newnode;
                }
                level--;
            }
        }
    }
    //从最高层开始找到小于key的前驱节点直到最后一层
    Node* mostRightLessNodeInTree(const K& key) {
        int level = maxLevel;//最高层
        Node* cur = head;//从头节点开始
        while (level >= 0)//直到最底层
        {
            cur = mostRightLessNodeLevel(key, cur, level--);
            //找到每一层的前驱节点用cur来接住
        }
        return cur;//返回cur
    }
    //获取当前层的前驱节点
    Node* mostRightLessNodeLevel(const K& key, Node* cur, int level) {
        Node* next = cur->nextNodes[level];//从第一个开始
        while (next && next->isKeyLess(key))//判断是否小于key如果小于就继续
        {
            //迭代往后走
            cur = next;
            next = cur->nextNodes[level];
        }
        return cur;//返回前区节点
    }

先找到前驱节点并插入,和单链表的插入类似.

2.2跳表的删除

删除的思路和插入的思路类似：

1.先判断当前节点是否存在，存在才删。

2.找到前驱节点

3.删除节点，与单链表的删除类似

假设我们要从跳表中删除结点10，首先我们按照跳表查找结点的方法，找到待删除的结点前驱节点：

下来，按照一般链表的删除方式，把结点10从原始链表当中删除：

这样是不是完了？不是我们还要将10的索引也一起删了。

这里又出现了一个问题，如果某一层的索引删光了，怎么办。直接将那一层给去掉。

刚才删除10之后第三层的索引已经删光了，将其删掉。

最终结果：

对应代码：

pair<K, V> get(K key) {//获取key所对应节点的值
        Node* less = mostRightLessNodeInTree(key);//前驱节点
        Node* next = less->nextNodes[0];//下一个

        return next && next->isKeyEqual(key) ? next->_kv : pair<K, V>();
    }
    bool containsKey(K key) {//判断是否存在key
        Node* less = mostRightLessNodeInTree(key);//找到前驱节点
        Node* next = less->nextNodes[0];//记录下一个
        return next && next->isKeyEqual(key);//看下一个是否相等
    }
    void Erase(K key) {
        if (containsKey(key)) {//看是否含有key
            --_size;//个数减一
            int level = maxLevel;//从最高层开始
            Node* prev = head;
            Node* tmp = nullptr;//记录被删除节点
            while (level >= 0) {
                prev = mostRightLessNodeLevel(key, prev, level);//找到前驱节点
                Node* next = prev->nextNodes[level];//记录前驱节点的下一个
                if (next && next->isKeyEqual(key)) {
                    //判断下一个是否是要删的节点，next为空说明这一层没有key对应的节点
                    tmp = next;//记录要删的节点
                    prev->nextNodes[level] = next->nextNodes[level];//改变链接关系
                    
                }
                //level层只剩下一个节点，默认为head,这一层已经没用了
                if (level != 0 && prev == head && prev->nextNodes[level] == nullptr) {

                    prev->nextNodes.pop_back();//去掉索引已经空的那一层
                    maxLevel--;//最大层数减减
                }
                level--;
            }
            delete tmp;//删除节点
        }
    }

对应总代码：

#pragma once
#include<vector>
#include<random>
#include<iostream>
using namespace std;

template<class K, class V>
struct SkipListNode
{
    SkipListNode(const pair<K, V>& kv, bool flag = true)
        :_kv(kv)
        , _flag(flag)

    {}
    bool isKeyLess(const K& othoerKey) {//判断当前节点是否小于otherkey
        return  _flag || othoerKey > _kv.first;
    }
    bool isKeyEqual(const K& key) {
        return  key == _kv.first;//判断key和当前节点是否相等

    }
    vector<SkipListNode<K, V>*>nextNodes;//存储指针
    pair<K, V>_kv;
    bool _flag;//标记是否为头节点
};

template<class K, class V>
class SkipListMap {
    typedef SkipListNode<K, V>Node;
public:
    SkipListMap() {
        head = new Node(pair<K, V>());
        head->nextNodes.push_back(nullptr);//先有第0层链表。
        _size = 0;
        maxLevel = 0;
    }
    void Insert(const pair<K, V>& kv) {

        Node* less = mostRightLessNodeInTree(kv.first);//找到前驱节点
        Node* Find = less->nextNodes[0];//如果已经存在那么下一个就是要插入的这个值
        if (Find && Find->isKeyEqual(kv.first)) {//先判断是否已经存在
            return;
        }
        else {//不存在
            _size++;//将个数++
            int newNodelevel = 0;//记录该节点会有几层
            
            int seed = time(0);
            static default_random_engine tmp(seed);//随机数
            
            while (tmp()%100/100.0000<PROBABILITY){//0.5的概率小于0.5就++直到大于0.5
                newNodelevel++;
            }
    

            while (newNodelevel > maxLevel) {
                //如果超过了头节点中的最大层数那么将头节点的层数增加到当前节点的层数
                head->nextNodes.push_back(nullptr);//插入nullptr
                maxLevel++;
            }
            Node* newnode = new Node(kv, false);//创建新节点
            for (int i = 0; i <= newNodelevel; i++) {
                newnode->nextNodes.push_back(nullptr);//一开始每一层的指针指向空
            }
            int level = maxLevel;//从最高的那一层开始
            Node* pre = head;
            while (level >= 0) {//直到最底层

                pre = mostRightLessNodeLevel(kv.first, pre, level);//找到前区节点
                if (level <= newNodelevel) {//如果层数比当前节点的层数要多不用指向我
                    //插入
                    newnode->nextNodes[level] = pre->nextNodes[level];
                    pre->nextNodes[level] = newnode;
                }
                level--;
            }
        }
    }
    //从最高层开始找到小于key的前驱节点直到最后一层
    Node* mostRightLessNodeInTree(const K& key) {
        int level = maxLevel;//最高层
        Node* cur = head;//从头节点开始
        while (level >= 0)//直到最底层
        {
            cur = mostRightLessNodeLevel(key, cur, level--);
            //找到每一层的前驱节点用cur来接住
        }
        return cur;//返回cur
    }
    //获取当前层的前驱节点
    Node* mostRightLessNodeLevel(const K& key, Node* cur, int level) {
        Node* next = cur->nextNodes[level];//从第一个开始
        while (next && next->isKeyLess(key))//判断是否小于key如果小于就继续
        {
            //迭代往后走
            cur = next;
            next = cur->nextNodes[level];
        }
        return cur;//返回前区节点
    }
    //V get(K key) {
    //    if (key == null) {
    //        return null;
    //    }
    //    SkipListNode<K, V> less = mostRightLessNodeInTree(key);
    //    SkipListNode<K, V> next = less.nextNodes.get(0);
    //    return next != null && next.isKeyEqual(key) ? next.val : null;
    //}
    pair<K, V> get(K key) {//获取key所对应节点的值
        Node* less = mostRightLessNodeInTree(key);//前驱节点
        Node* next = less->nextNodes[0];//下一个

        return next && next->isKeyEqual(key) ? next->_kv : pair<K, V>();
    }
    bool containsKey(K key) {//判断是否存在key
        Node* less = mostRightLessNodeInTree(key);//找到前驱节点
        Node* next = less->nextNodes[0];//记录下一个
        return next && next->isKeyEqual(key);//看下一个是否相等
    }
    void Erase(K key) {
        if (containsKey(key)) {//看是否含有key
            --_size;//个数减一
            int level = maxLevel;//从最高层开始
            Node* prev = head;
            Node* tmp = nullptr;//记录被删除节点
            while (level >= 0) {
                prev = mostRightLessNodeLevel(key, prev, level);//找到前驱节点
                Node* next = prev->nextNodes[level];//记录前驱节点的下一个
                if (next && next->isKeyEqual(key)) {
                    //判断下一个是否是要删的节点，next为空说明这一层没有key对应的节点
                    tmp = next;//记录要删的节点
                    prev->nextNodes[level] = next->nextNodes[level];//改变链接关系
                    
                }
                //level层只剩下一个节点，默认为head,这一层已经没用了
                if (level != 0 && prev == head && prev->nextNodes[level] == nullptr) {

                    prev->nextNodes.pop_back();//去掉索引已经空的那一层
                    maxLevel--;//最大层数减减
                }
                level--;
            }
            delete tmp;//删除节点
        }
    }
private:
    const double PROBABILITY = 0.5;//0.5的概率
    Node* head;//头节点
    int _size;//个数
    int maxLevel;//最大的层数
};

3.letecode测试及其链接

对应letecode链接：

设计跳表 - 力扣（LeetCode） (leetcode-cn.com)

题目描述：

不使用任何库函数，设计一个跳表。

跳表是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

例如，一个跳表包含 [30, 40, 50, 60, 70, 90] ，然后增加 80、45 到跳表中，以下图的方式操作：
Artyom Kalinin [CC BY-SA 3.0], via Wikimedia Commons

跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

了解更多 : https://en.wikipedia.org/wiki/Skip_list

在本题中，你的设计应该要包含这些函数：

bool search(int target) : 返回target是否存在于跳表中。
void add(int num): 插入一个元素到跳表。
bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回false. 如果存在多个 num ，删除其中任意一个即可。
注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

示例 1:

输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]

解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0); // 返回 false
skiplist.add(4);
skiplist.search(1); // 返回 true
skiplist.erase(0); // 返回 false，0 不在跳表中
skiplist.erase(1); // 返回 true
skiplist.search(1); // 返回 false，1 已被擦除

提示:

0 <= num, target <= 2 * 104
调用search, add, erase操作次数不大于 5 * 104 。

对应代码：

letecode上测试的是整形，而在这里实现的是泛型是任意类似，铁子们只要稍微改一下即可，在这里就只给出代码：

class Skiplist {
public:
struct SkipListNode
{
    SkipListNode(int kv, bool flag = true)
        :_kv(kv)
        , _flag(flag)

    {}
    bool isKeyLess(const int & othoerKey) {
        return  _flag || othoerKey > _kv;
    }
    bool isKeyEqual(const int & key) {
        return  key == _kv;

    }
    vector<SkipListNode*>nextNodes;
    int _kv;
    bool _flag;
};
typedef SkipListNode Node;
    Skiplist() {
    head = new Node(-1);
        head->nextNodes.push_back(nullptr);//先有第0层链表。
        _size = 0;
        maxLevel = 0;
    }
    
    bool search(int key) {
           Node* less = mostRightLessNodeInTree(key);
        Node* next = less->nextNodes[0];
        return next && next->isKeyEqual(key);  
    }
    
    void add(int num) {
           Node* less = mostRightLessNodeInTree(num);
        Node* Find = nullptr;
        if (Find && Find->isKeyEqual(num)) {
            return;
        }
        else {
            _size++;
            int newNodelevel = 0;
            
            int seed = time(0);
            static default_random_engine tmp(seed);
            
            while (tmp()%100/100.0000<PROBABILITY){
                newNodelevel++;
            }
    

            while (newNodelevel > maxLevel) {
                head->nextNodes.push_back(nullptr);
                maxLevel++;
            }
            Node* newnode = new Node(num, false);
            for (int i = 0; i <= newNodelevel; i++) {
                newnode->nextNodes.push_back(nullptr);
            }
            int level = maxLevel;
            Node* pre = head;
            while (level >= 0) {

                pre = mostRightLessNodeLevel(num, pre, level);
                if (level <= newNodelevel) {
                    newnode->nextNodes[level] = pre->nextNodes[level];
                    pre->nextNodes[level] = newnode;
                }
                level--;
            }
        }
    }
    
    bool erase(int key) {
if (containsKey(key)) {//看是否含有key
            --_size;
            int level = maxLevel;
            Node* prev = head;
            Node*tmp=nullptr;
            while (level >= 0) {
                prev = mostRightLessNodeLevel(key, prev, level);
                Node* next = prev->nextNodes[level];
                if (next && next->isKeyEqual(key)) {
                  tmp=next;
                    prev->nextNodes[level] = next->nextNodes[level];
                
                }
                //level层只剩下一个节点，默认为head,这一层已经没用了
                if (level != 0 && prev == head && prev->nextNodes[level] == nullptr) {

                    prev->nextNodes.pop_back();
                    maxLevel--;
                }
                level--;
            }
            delete tmp;
            return true;
        }
        
            return false;
        

    }
    Node* mostRightLessNodeInTree(const int & key) {
        int level = maxLevel;
        Node* cur = head;
        while (level >= 0)
        {
            cur = mostRightLessNodeLevel(key, cur, level--);
        }
        return cur;
    }
    Node* mostRightLessNodeLevel(const int & key, Node* cur, int level) {
        Node* next = cur->nextNodes[level];
        while (next && next->isKeyLess(key))
        {
            cur = next;
            next = cur->nextNodes[level];
        }
        return cur;
    }
    bool containsKey(int  key) {
        Node* less = mostRightLessNodeInTree(key);
        Node* next = less->nextNodes[0];
        return next && next->isKeyEqual(key);
    }
private:
    const double PROBABILITY = 0.5;
    Node* head;
    int _size;
    int maxLevel;
};

/**
 * Your Skiplist object will be instantiated and called as such:
 * Skiplist* obj = new Skiplist();
 * bool param_1 = obj->search(target);
 * obj->add(num);
 * bool param_3 = obj->erase(num);
 */

最后如果觉得对您有帮助的话，劳烦您动动您的手点个赞！谢谢。

标签：数据结构链表 java

本文转载自: https://blog.csdn.net/qq_56999918/article/details/122960821
版权归原作者 一个山里的少年 所有，如有侵权，请联系我们删除。

数据结构之跳表（含代码实现）

1.跳表的相关概念

2.跳表节点的定义及其实现

2.1跳表的插入

2.2跳表的删除

3.letecode测试及其链接

发表评论

“数据结构之跳表（含代码实现）”的评论:

关于作者

overfit同步小助手

相关阅读

文章导航